XYZ翼

描述

XYZ翼和 XY翼 很像：都是“一个枢纽 + 两个翼”的结构，用反证来删掉某个共同候选数。
不同点在于：XYZ翼的枢纽格有 3 个候选数，所以删数点通常需要同时看见枢纽格和两翼（因为共同候选数也可能直接落在枢纽格里）。

它的结构长这样（只盯住共同候选 z）：

• 枢纽格（蓝色）：候选 x、y、z
• 两翼（黄色）：分别是 {x、z} 和 {y、z}

结论：所有同时看见枢纽格和两翼的格子里，候选 z 都可以删除。

---

详解

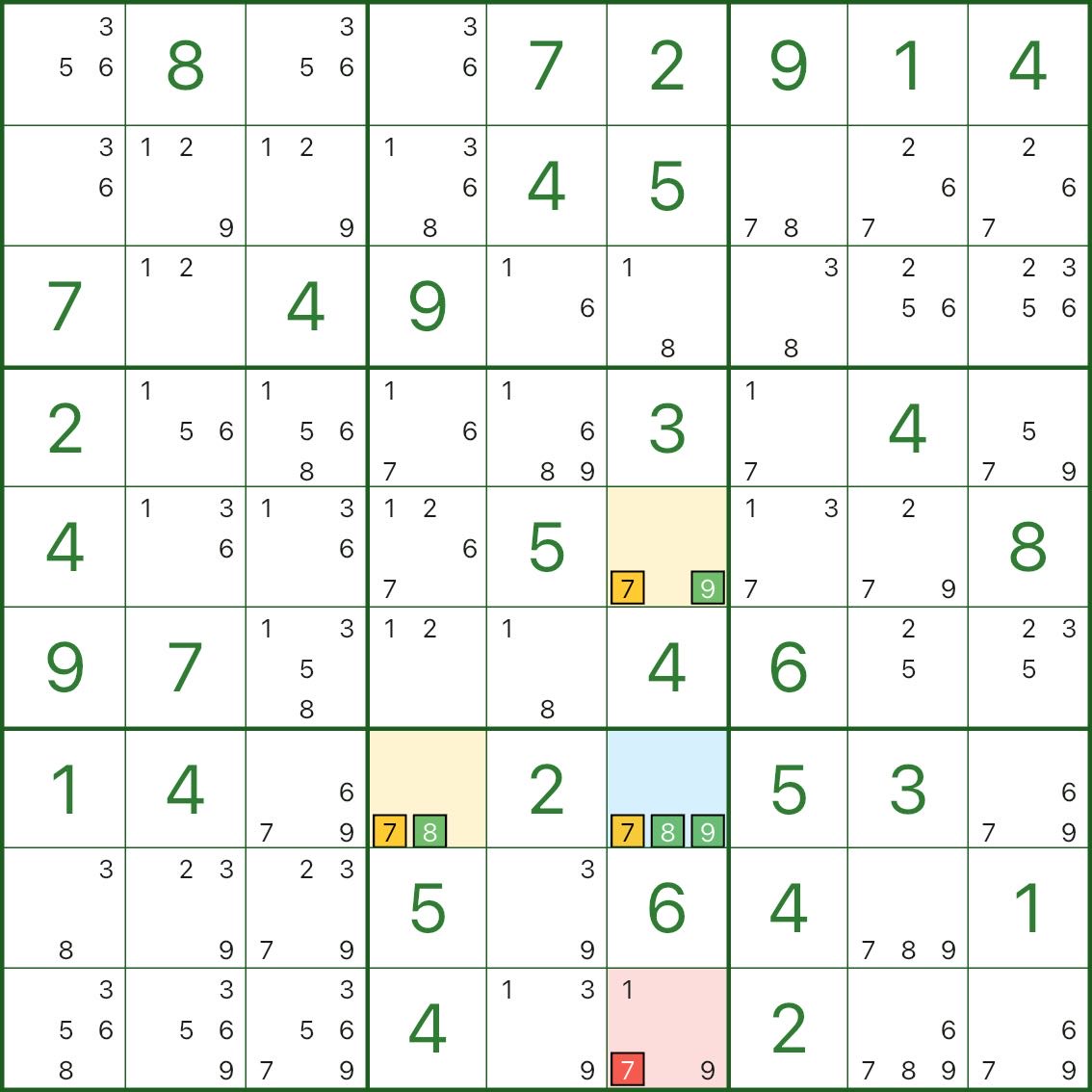
先看上图：要删除的是 r9c6 里的候选数字 7（红色）。
蓝色枢纽是 r7c6，它的候选是 7、8、9。
两条黄色翼分别是：

• r5c6：候选 7、9
• r7c4：候选 7、8

为什么 r9c6 中的 7 能删？看一个很短的反证就够了：

• 假设 r9c6 = 7（红色候选为真）
• r9c6 能同时看见两翼，所以两翼里的 7 都会被排除：
  • r5c6 只能变成 9
  • r7c4 只能变成 8
• 这样一来，枢纽格 r7c6 就麻烦了：
  • r9c6 = 7 ⇒ r7c6 不能是 7（同一列冲突）
  • r5c6 = 9 ⇒ r7c6 不能是 9（同一列冲突）
  • r7c4 = 8 ⇒ r7c6 不能是 8（同一行冲突）
  • r7c6 原本只有 {7、8、9}，全部被排除 ⇒ 无数可填（矛盾）

所以假设不成立：r9c6 不能是 7，候选数字 7 可以删除。

---

例子

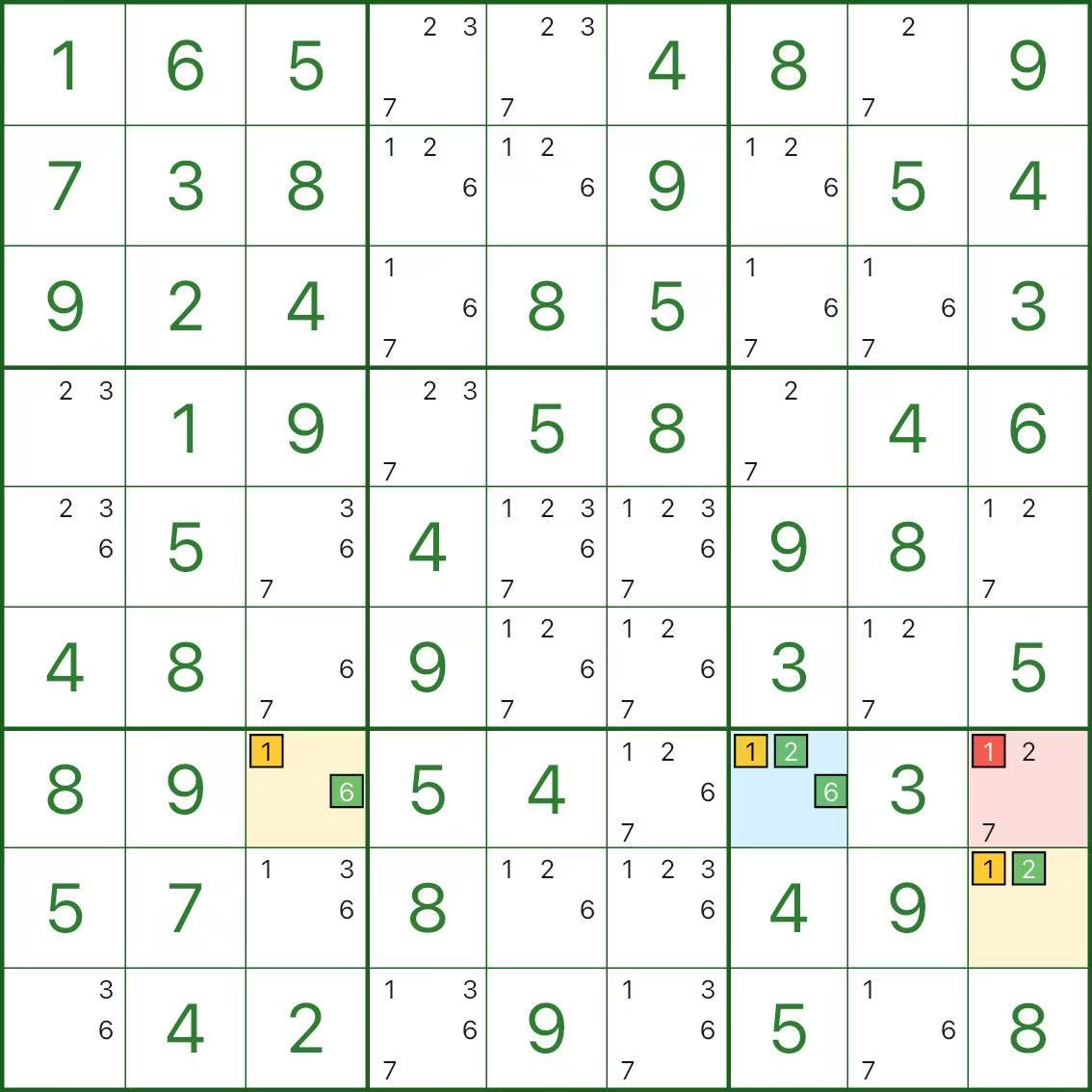
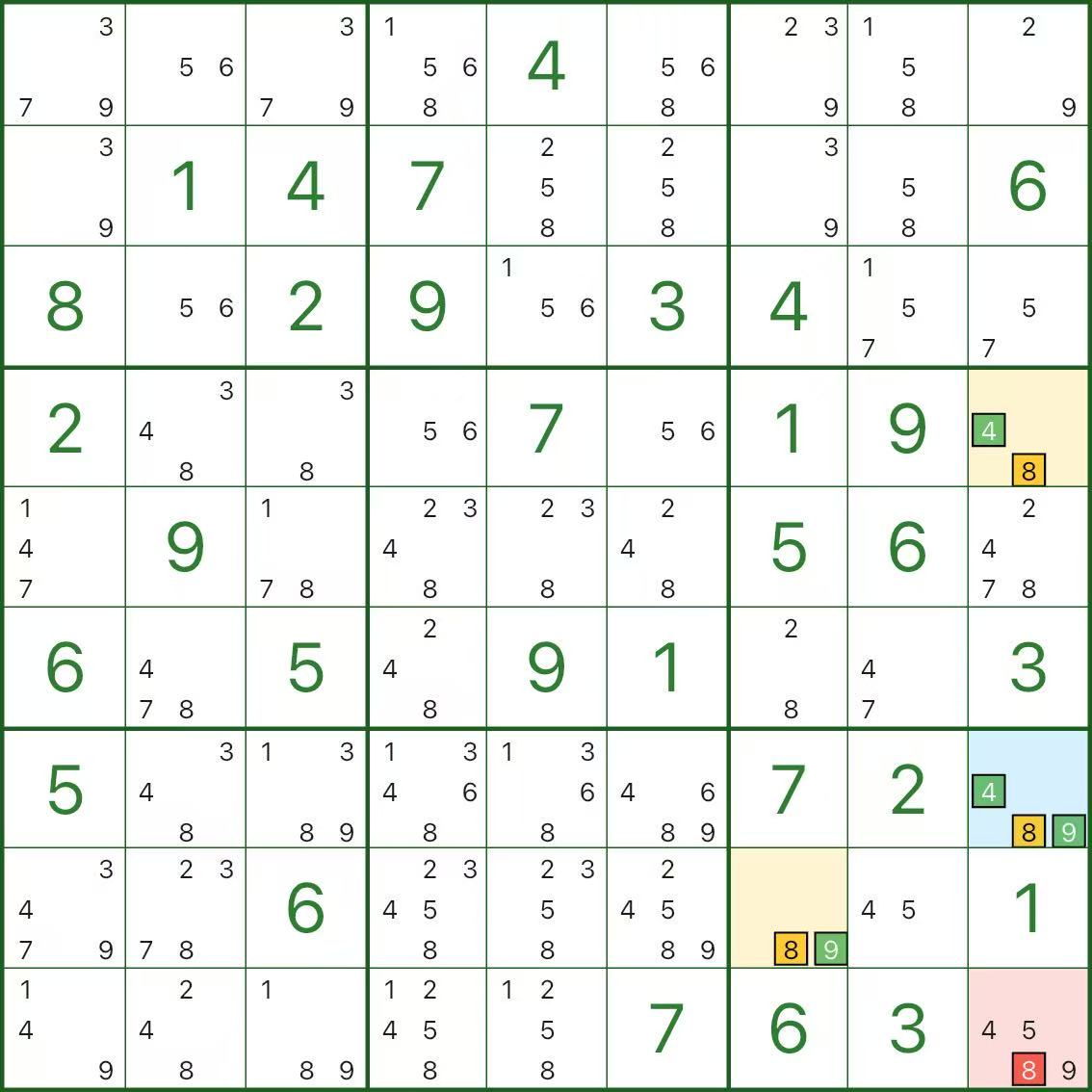
下面两张图是其他 XYZ翼 的例子，你可以直接对照“枢纽（蓝）/ 两翼（黄）/ 删数（红）”的结构来观察：

---

如何寻找 XYZ翼？

一句话：先找一个三候选枢纽 {x、y、z}，再找两条双值翼 {x、z}、{y、z}，最后删掉“同时看见枢纽和两翼”的 z。

在游戏里你可以按这个顺序找：

1. 找一个候选数是 3 个的格子当枢纽（蓝色）
2. 在它的可见范围内，找两格当翼（黄色），它们都只有 2 个候选数，并且分别形如 {x、z}、{y、z}
3. 找到一个格子能同时看见枢纽和两翼：如果它里有候选 z，通常就是删数点（红色）