WXYZ翼

如果你已经看过这两篇，会更容易理解 WXYZ翼：
XY翼 / XYZ翼

---

1. 描述

WXYZ翼可以理解为 XY翼/XYZ翼 的“加大版”：还是用一个小结构，把某个候选逼到矛盾，从而删数。

它通常表现为一小团彩色格子（蓝色枢纽格 + 黄色翼）：

• 这团结构里所有候选数加起来，只涉及 4 个数字（比如 {1,4,7,9}）
• 如果我们假设某个红色候选 d 为真，它会把结构里其它位置的 d 都排除掉
• 结构里就只剩 3 个数字要填进 4 个格子
  • ⇒ 必然有格子“无数可填”（矛盾）

所以红色候选 d 可以删除。

---

2. 详解

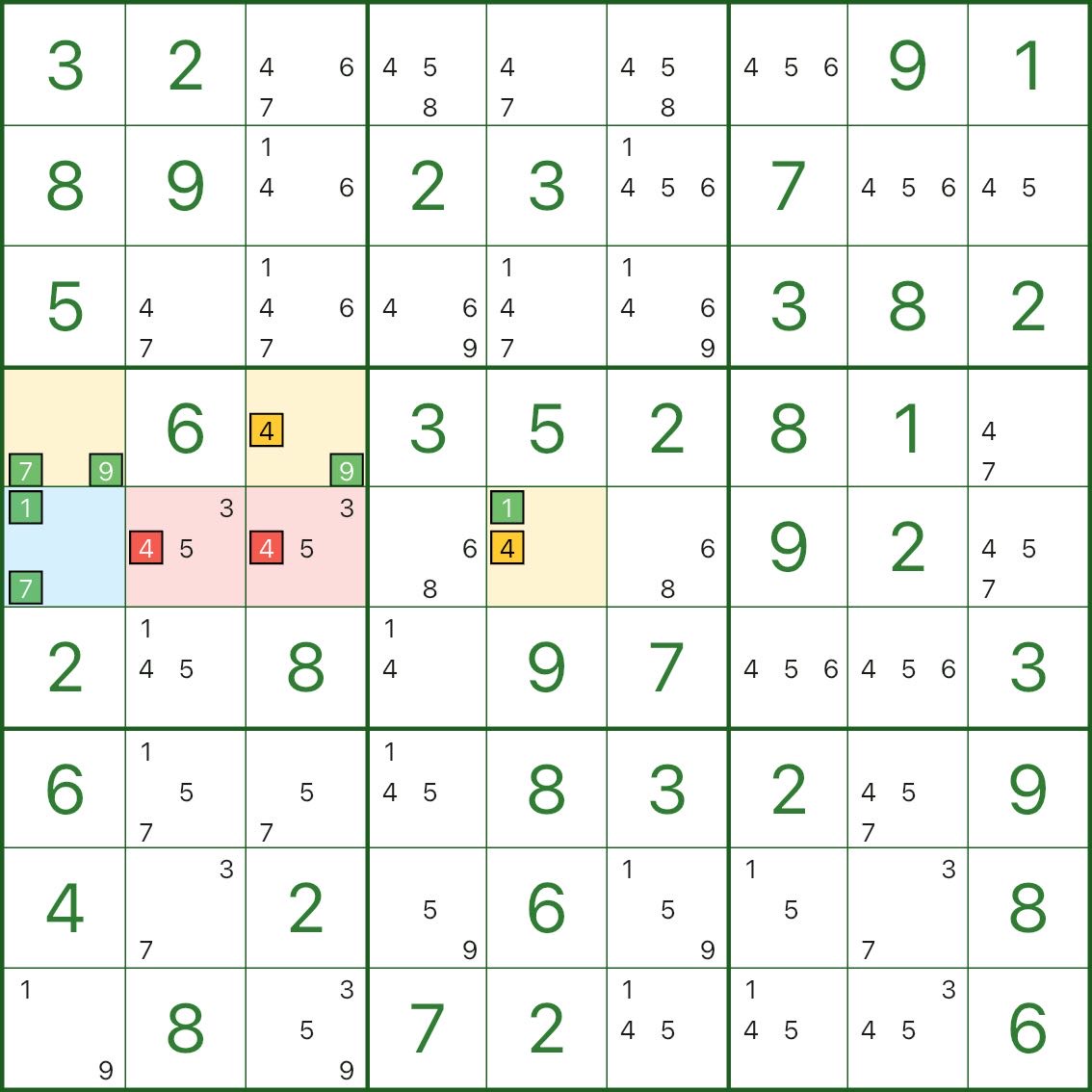
先看上图：蓝色是枢纽格，黄色是翼，红色是删数格。要删除的是红色格子里的候选数字 4（r4c2、r4c3）。

为什么红色的 4 能删？看一个很短的反证就够了：

• 假设红色格子里 4 为真
• 这样一来，黄色翼中与它冲突的 4 都会被排除
• 黄色翼就会被迫只能在 1、7、9 之间分配（上图中已经用绿色候选数标出了这些数字）
• 但蓝色枢纽格本来也只剩 1、7 这些候选
  当翼被迫占用/封锁了 1、7、9，枢纽格就会变成 无数可填（矛盾）

所以假设不成立：红色格子里的候选数字 4 可以删除。

---

3. 例子

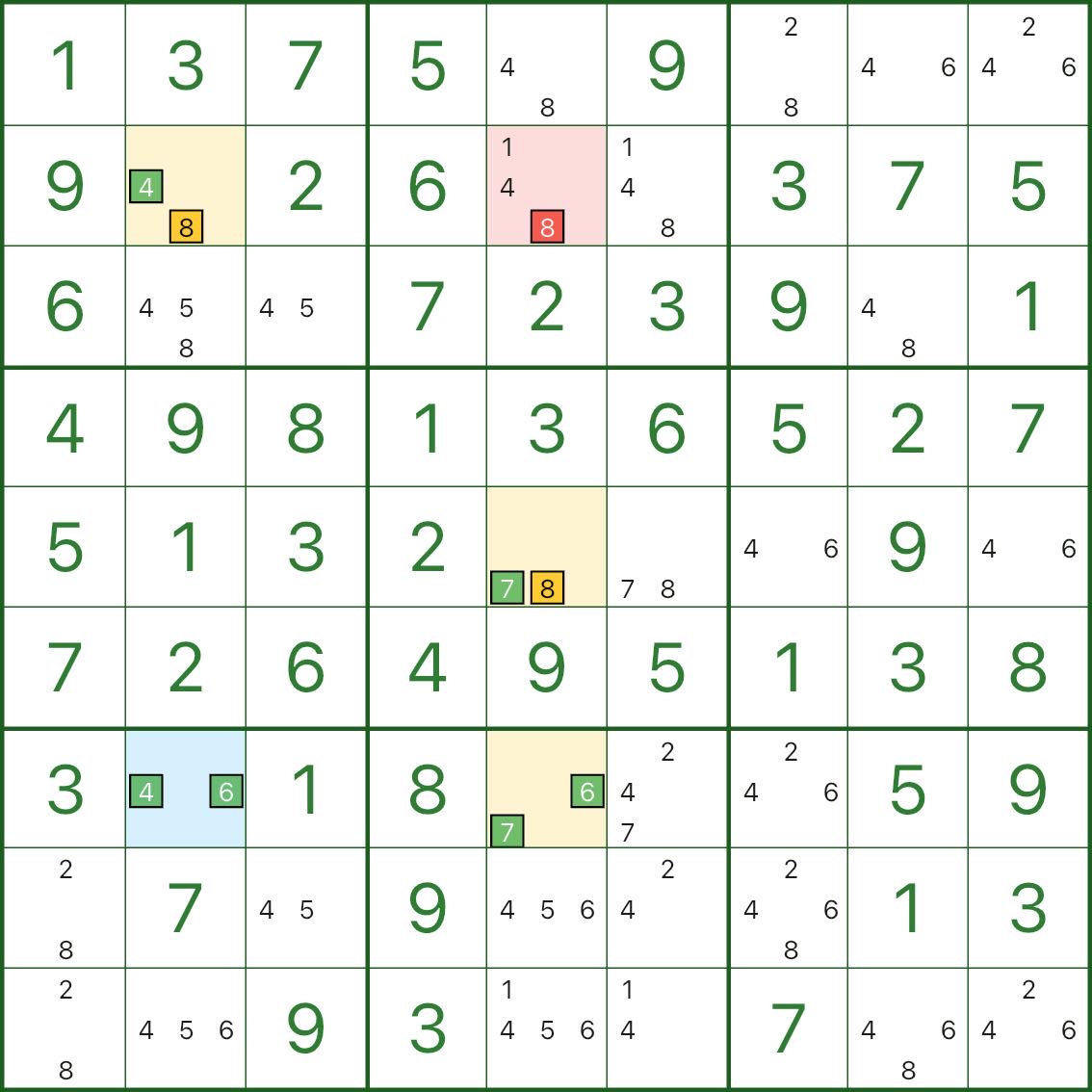
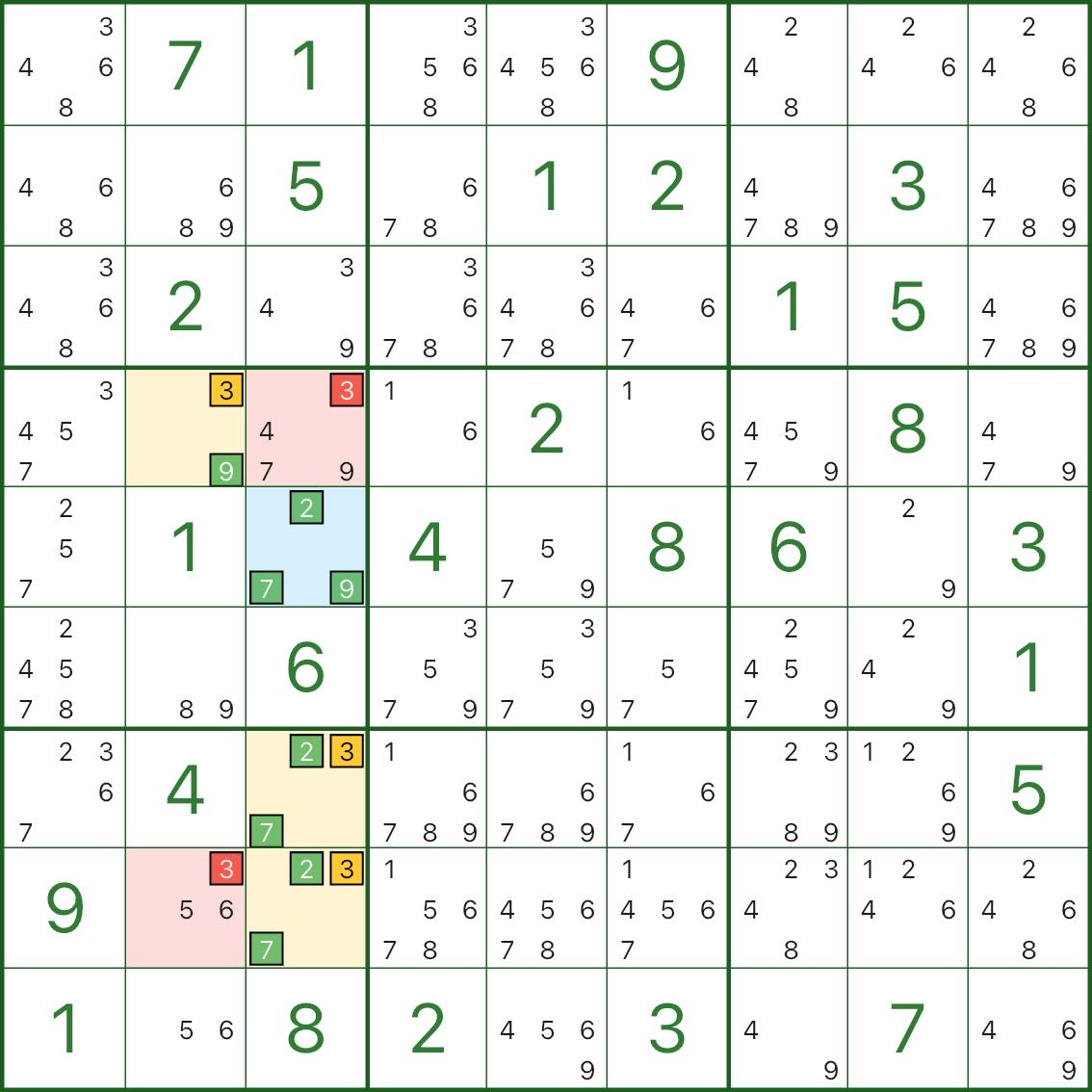
下面两张图是其它 WXYZ翼 的例子，你可以直接对照“蓝色枢纽格 / 黄色翼 / 红色删数格”的结构来观察：

---

4. 如何寻找 WXYZ翼？

一句话：先找到一团蓝黄结构只涉及 4 个数字，再从红色候选出发做一次反证——如果它为真会让蓝黄结构里出现“无数可填”，那它就能删除。

在游戏里你可以按这个顺序找：

1. 先留意一团相邻或互相可见的彩色结构（蓝色 + 黄色）
2. 看看它们的候选数加起来，是不是只落在 4 个数字里
3. 再看红色删数点：假设它为真时，结构中某个数字会被“挤掉”，最终导致结构里至少有一个格子无数可填
4. 矛盾成立就可以删数