刺身鱼

前置知识：X翼（二阶鱼） · 带鳍X翼

描述

刺身鱼（也叫“退化鱼”）是一种“删候选”的鱼类技巧。你可以把它理解成： 带鳍鱼的“更不完整版本”——绿色的鱼身还没完全形成标准鱼，但因为鱼鳍（黄色）都落在同一宫里，我们仍然能推出一小块稳定的删数结论。

它通常有三个关键点：

• 鱼身（绿）：看起来像要组成一条标准鱼，但会缺一角/缺一条覆盖线
• 鱼鳍（黄）：多出来的同数字候选，而且必须都在同一宫
• 删数（红）：多发生在“鱼鳍所在宫”里（范围比标准鱼更小）

---

详解

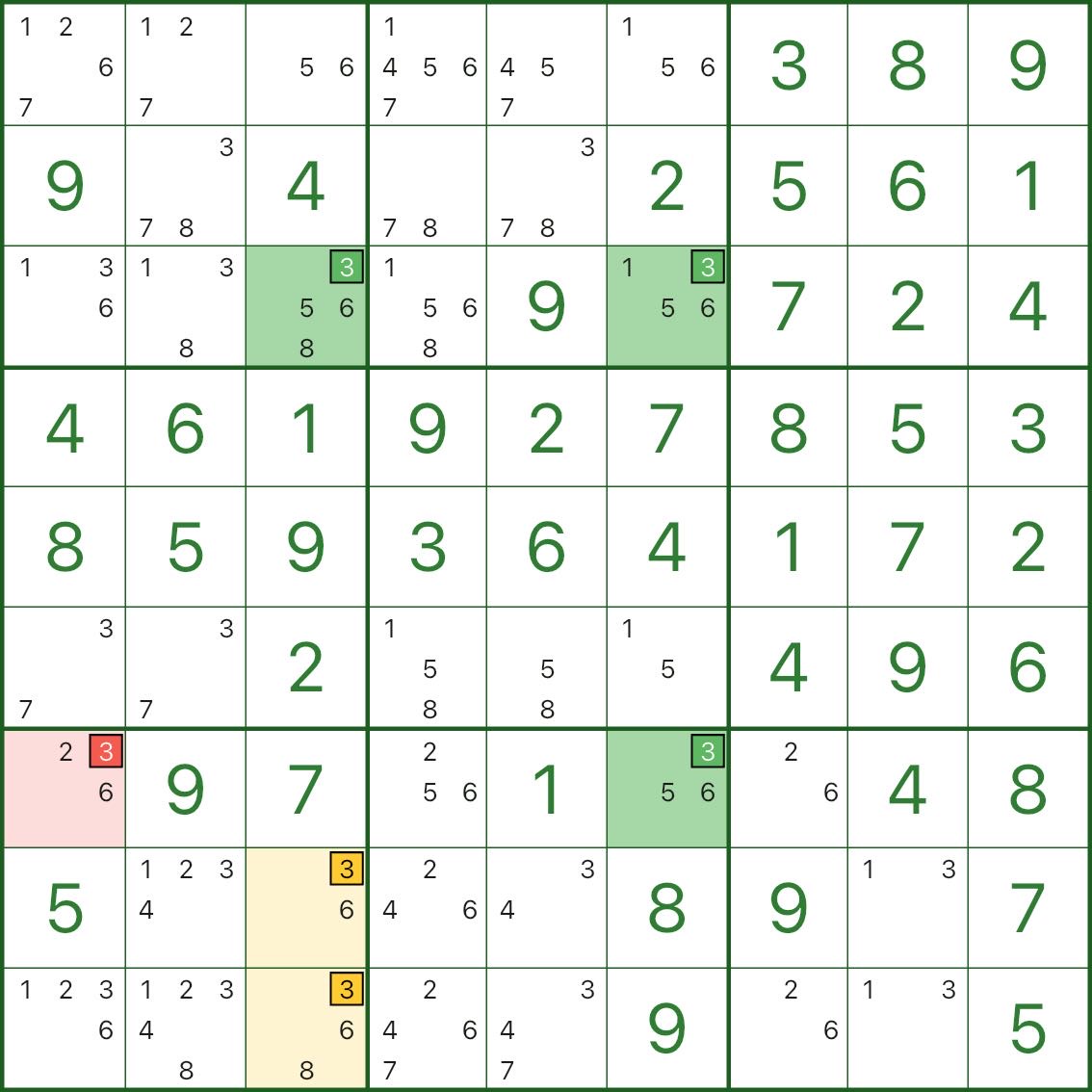
先看上图：目标数字是 3。

• 绿色鱼身候选在 r3c3、r3c6、r7c6
• 黄色鱼鳍在 r8c3、r9c3（都在同一宫）
• 红色要删除的是 r7c1 里的候选数字 3

为什么 r7c1 里的候选数字 3 能删？我们做一个很短的反证：

1. 假设 r7c1 = 3（红色为真）
   因为 r7c1 和鱼鳍 r8c3、r9c3 在同一宫，所以这两个鱼鳍里的 3 都必须为假。

2. 再看第 3 列：在上图里，候选数字 3 只剩下 r3c3、r8c3、r9c3
   现在鱼鳍 r8c3、r9c3 都被排除了，所以 r3c3 只能是 3。

3. r3c3 = 3 会让 r3c6 不能是 3（同一行冲突）。
   而第 6 列里，候选数字 3 只出现在 r3c6、r7c6 两处，所以 r3c6 不是 3 ⇒ r7c6 必须是 3。

4. 这就出现矛盾了：我们一开始假设 r7c1 = 3，同时又被迫得到 r7c6 = 3，
   同一行出现两个 3 不可能成立。

因此假设不成立：r7c1 里的候选数字 3 可以删除。

---

例子

下面这张图是另一个刺身鱼的例子，你可以直接对照“鱼身（绿）/ 鱼鳍（黄）/ 删数（红）”来观察：

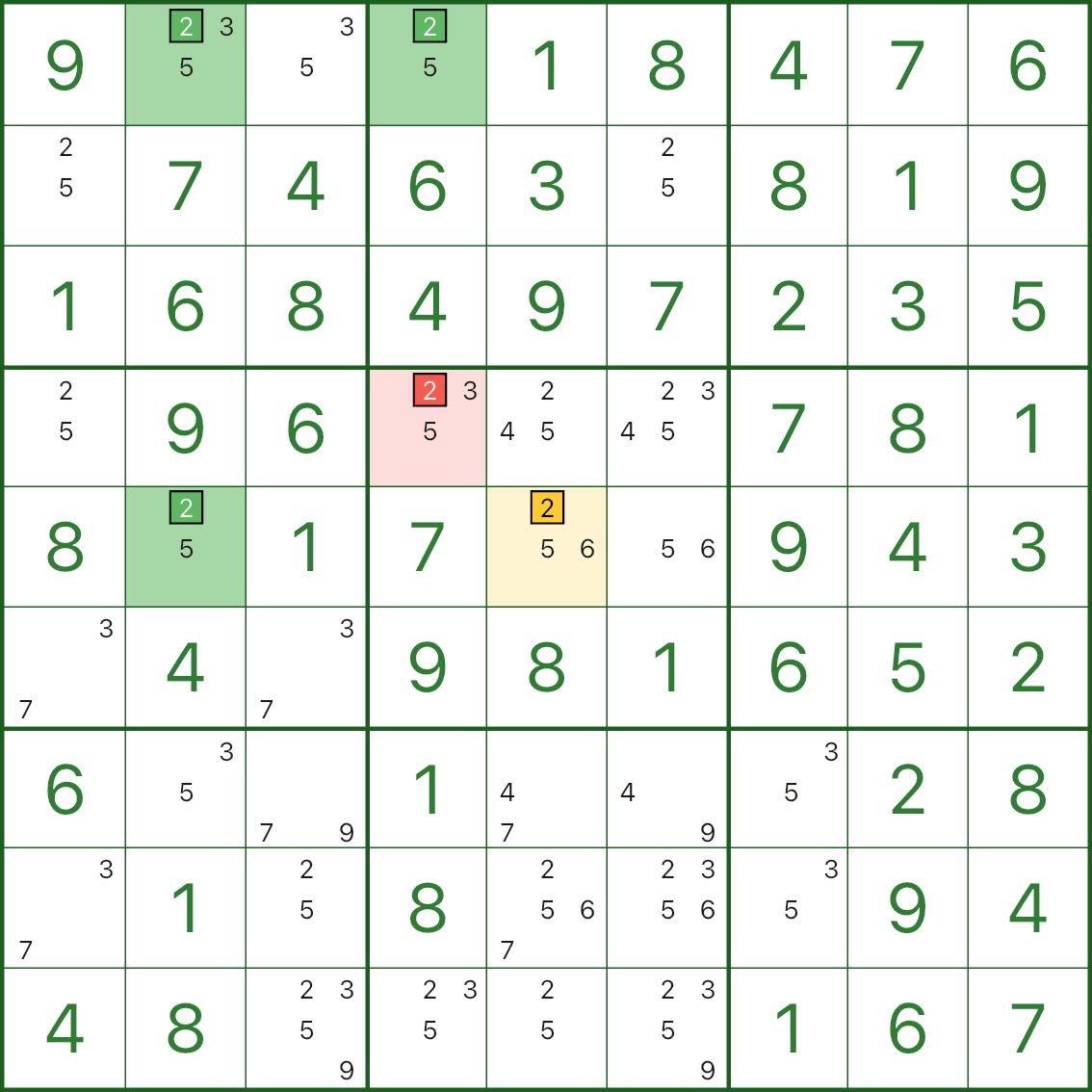
刺身剑鱼、刺身水母也是一样道理：只是鱼的阶数更高、渔网更大，但核心仍然是“鱼身不完整 + 鱼鳍同宫 ⇒ 小范围删数”。

---

如何寻找刺身鱼？

一句话：先看到“缺一角的鱼身”，再确认鱼鳍同宫，最后只在鱼鳍所在宫里找删数。

在游戏里你可以按这个顺序找：

1. 先选一个数字 d
2. 像找标准鱼一样，找出“看起来能对齐”的鱼身（绿），但它会明显缺一角/缺一条覆盖线
3. 找到多出来的同数字候选（黄），并确认所有鱼鳍都落在同一宫
4. 删数优先看“鱼鳍所在宫”里的候选 d（通常就在红色标注的位置）