技巧文档 / 数对和数组
数对和数组
显性/隐性数对数组
入门
数对和数组
显性/隐性数对数组
数对和数组是一类非常实用的“删候选”技巧。它们看起来名字很多,但本质都在做同一件事:
在同一行、同一列或同一宫(下面统称为一个 区域)里,某几格和某几个数字互相“占位”锁定了,于是其它地方就不可能了。
你不需要背术语,记住这个直觉就够了:
- 显性:从“格子里写了什么”出发(这几格只剩这些数)
- 隐性:从“这个数字能去哪”出发(这几个数只剩这些格)
1. 显性数对(Naked Pair)
当同一个区域里,有两格都只剩下同一对候选数(比如 a、b),就形成显性数对。
这意味着:
- 这两格必然一格是 a,一格是 b(顺序不确定)
- 所以这个区域里其它空格不可能再是 a 或 b,可以把对应候选删掉
先看下图:请把注意力放在高亮的第三宫,以及两个绿色格子 r2c9、r3c9。
你会发现:它们的候选数都只剩 1、5。
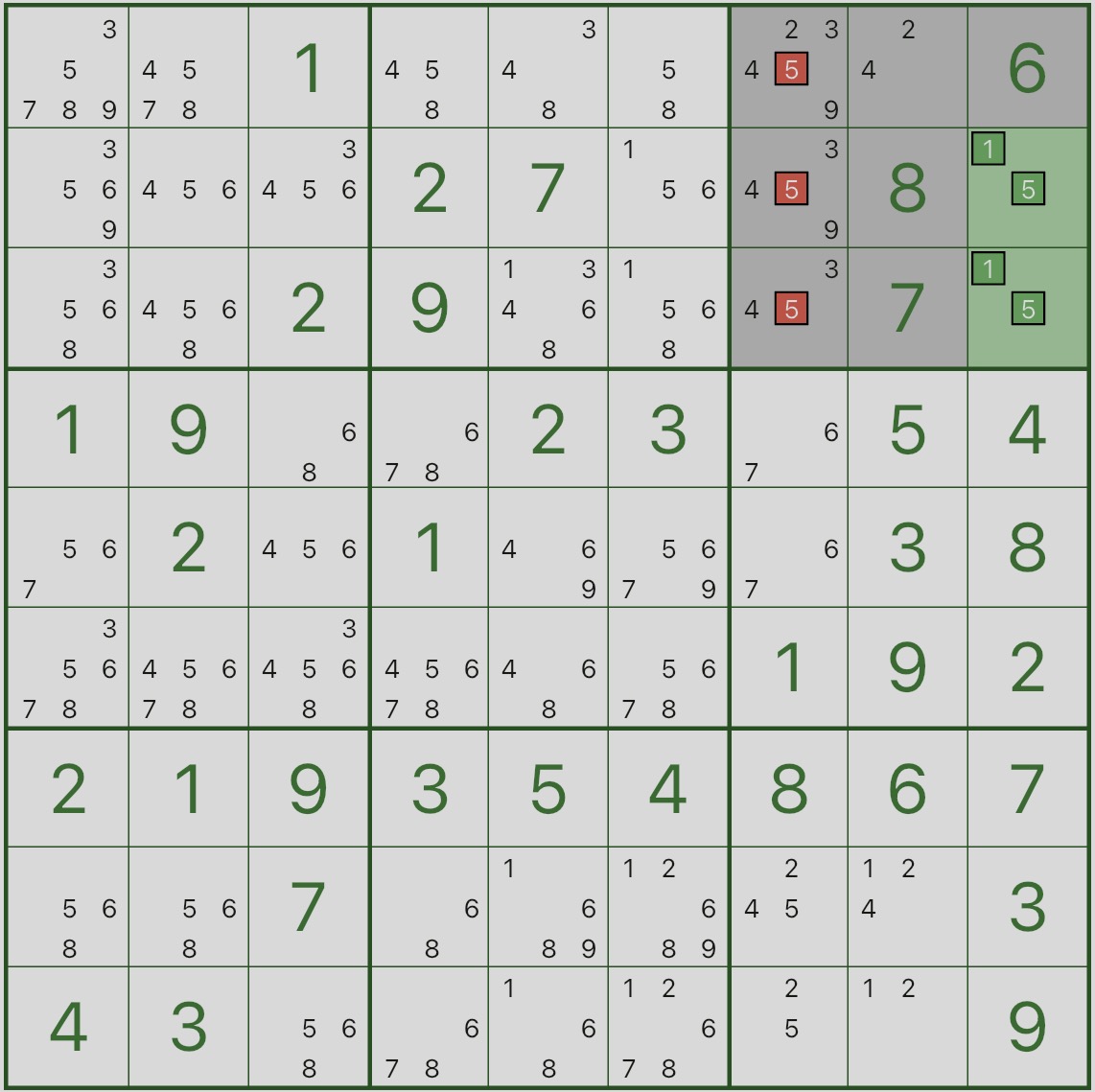
这表示:在第三宫里,数字 1、5 必须由 r2c9 和 r3c9 来“占位”。
图中标红的候选数,就是这一步可以删除的候选。
再看红色候选:r1c7、r2c7、r3c7 里的候选数字 5 都可以删除。
理由用一个反证就能看懂:
- 假设 r1c7 中的候选 5 为真(r2c7、r3c7 同理)
- 那么第三宫里已经放了一个 5,绿色格子 r2c9、r3c9 就都不能再是 5,只能被迫填 1
- 可是 r2c9 和 r3c9 在同一列(第 9 列),不可能同时都是 1 —— 矛盾
⇒ 红色的候选 5 都可以安心删掉
2. 隐性数对(Hidden Pair)
当同一个区域里,候选数 a 只出现在两格中,同时候选数 b 也只出现在同样两格中,就形成隐性数对。
注意:这两格里可能还有别的候选数,但 a、b 已经被锁定只能落在这两格里。
所以我们可以:
- 把这两格里 除 a、b 之外的其它候选数删掉
先看下图:请把注意力放在高亮的第 4 列。
把候选数字 4 和 5 在这一列里出现的位置找出来,你会发现它们只出现在 r1c4 和 r6c4。
这表示:第 4 列里的 4、5 必须由 r1c4 和 r6c4 来放。
图中标红的候选数,就是这一步可以删除的候选。
所以我们可以删掉 r1c4、r6c4 里除 4、5 以外的其它候选。原因同样很直觉:
- 假设 r1c4 填了一个不是 4 或 5 的数字
- 那么 4 和 5 就只剩 r6c4 这一个格子可以放
- 可一个格子不可能同时放 4 和 5 —— 矛盾
⇒ r1c4、r6c4 只能是 4 或 5,其它候选都可以删除
3. 显性数组(Naked Triple / Quad)
把“显性数对”推广一下:
在同一个区域里,如果 N 个格子的候选数合起来只包含 N 个数字(例如 3 格只包含 a、b、c),就形成显性三数组;4 格同理是显性四数组。
这意味着这 N 个数字只能在这 N 格里互相分配,所以:
- 这个区域里其它空格的这些数字(例如 a、b、c)都可以删掉
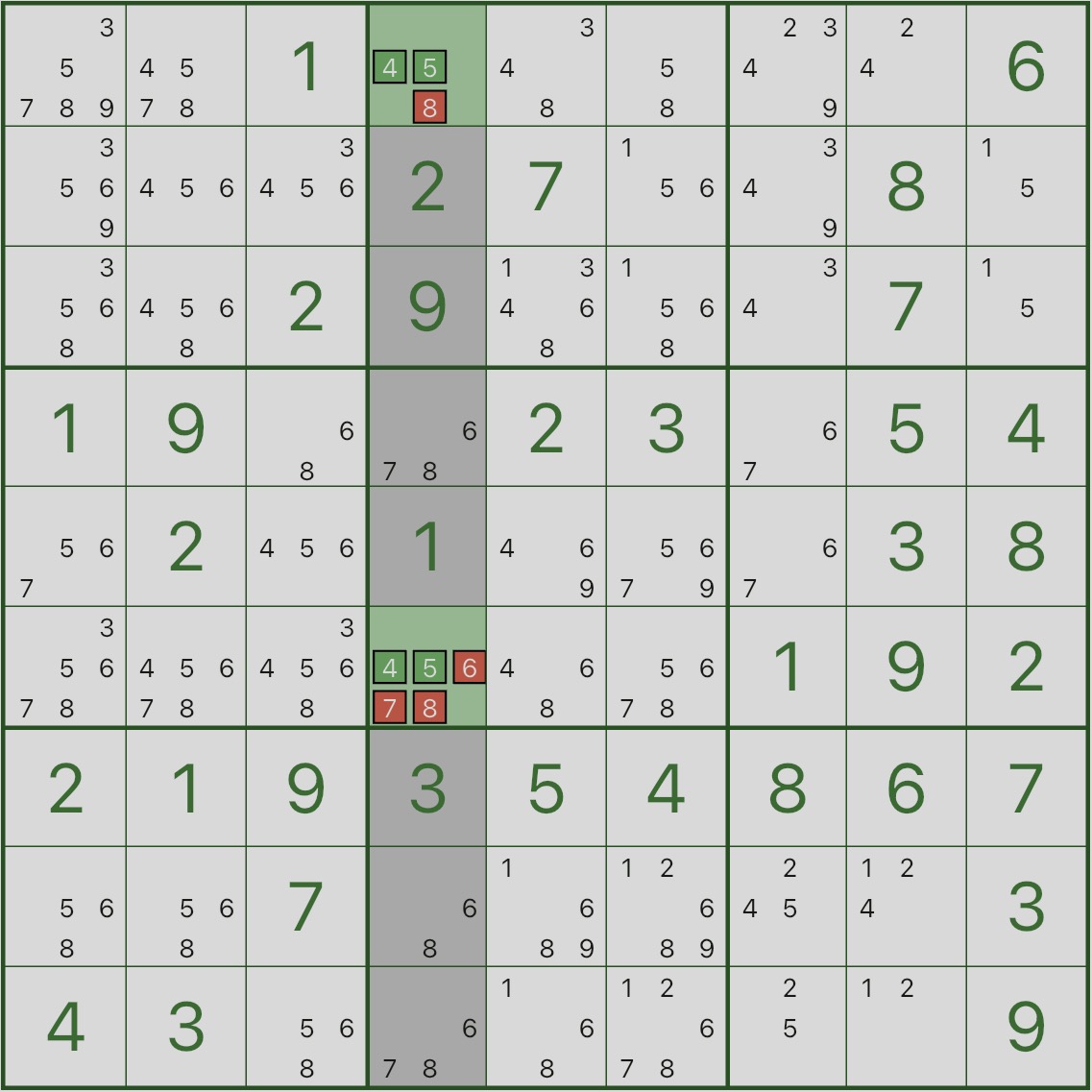
先看下图:请把注意力放在高亮的第 8 行,以及 r8c1、r8c2、r8c4 这三个格子。
你会发现:它们的候选数合起来只包含 5、6、8。

这表示:第 8 行里的 5、6、8 必须由 r8c1、r8c2、r8c4 来分配。
图中标红的候选数,就是这一步可以删除的候选。
因此第 8 行其它格子里标红的 5、6、8 都可以删掉。
反证的直觉是:
- 假设你在第 8 行的别的格子里“占走”了 5、6、8 其中一个
- 那么这三个格子就只剩下 2 个数字去填 3 个格子
- 无论怎么填都会出现重复或无解 —— 矛盾
4. 隐性数组(Hidden Triple / Quad)
把“隐性数对”推广一下:
在同一个区域里,如果某 N 个数字只出现在同样的 N 个格子里(即使这些格子里还有其它候选数),就形成隐性三数组或四数组。
这意味着这 N 个数字被锁定只能落在这 N 格里,所以:
- 这 N 个格子里 除这 N 个数字之外的其它候选数都可以删掉
先看下图:请把注意力放在高亮的第 5 列。
你会发现:候选数字 4、7、8 只出现在 r1c5、r8c5、r9c5。

这表示:第 5 列里的 4、7、8 必须由 r1c5、r8c5、r9c5 来放。
图中标红的候选数,就是这一步可以删除的候选。
所以我们可以把这三个格子里除 4、7、8 之外的其它候选全部删掉。
原因同样很直觉:
- 假如其中任意一个格子填了别的数字
- 那么 4、7、8 就会“挤不下”(只剩 2 格却要放 3 个数字)—— 矛盾
5. 更容易找到的小建议
- 先把候选数尽量写完整(难题里几乎离不开它)
- 先扫显性:从“候选数特别少”的格子开始看(2、3 或 4 个候选最醒目)
- 再扫隐性:在一个区域里,看看某个数字是不是“只剩两格、三格或四格能放”
- 删完候选后别急着走:回头看一眼是否出现了“只剩一个候选”的格子,或“某个数字只剩一个位置”