3D 美杜莎（进阶染色）

前置知识：基础染色

描述

3D 美杜莎可以理解成“基础染色的升级版”：同样用蓝/黄两色把候选数分成两条互斥的推导路线，但它不再只盯一个数字，而是把多个数字也一起串进来做推理。

它之所以更强，是因为它的“强关系”不止一种：

• 共轭对（强链）：在同一行/列/宫里，某个数字只剩 2 个候选位置
• 双值格（强链）：某个格子里只剩 2 个候选数字

沿着这些强链染色后，你可以把蓝/黄理解成两种互斥的假设：

• 假设蓝色为真 ⇒ 黄色为假
• 假设蓝色为假 ⇒ 黄色为真

也就是说：在同一条染色链里，蓝黄必有一种为真。

3D 美杜莎最常见的两种结论是：

1. 陷阱（Trap）：一个红色候选同时与“蓝色链”和“黄色链”冲突 → 红色候选可以删除
2. 同色冲突：同一行/列/宫（或同一格）里出现两个同色候选 → 这个颜色整条推导链都不成立，可以整链删除

如果你对“强链/弱链、强弱交替”还不熟，建议先读：链的基础。

---

陷阱

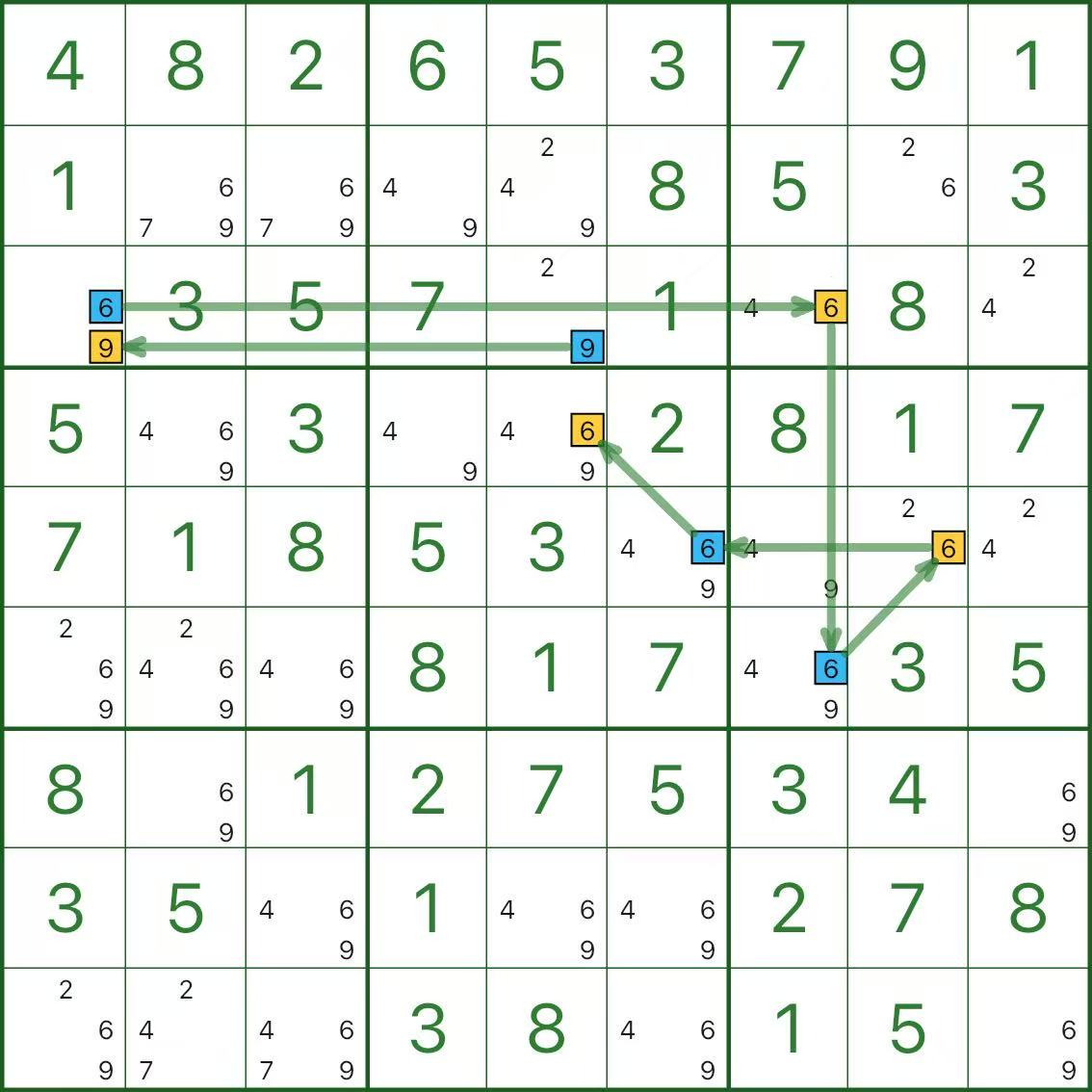
先看上图：我们沿着强链把候选数染成蓝/黄两色，其中起点是 r3c5 中的候选数字 9（蓝色），并且推导到 r4c5 中的候选数字 6（黄色）。

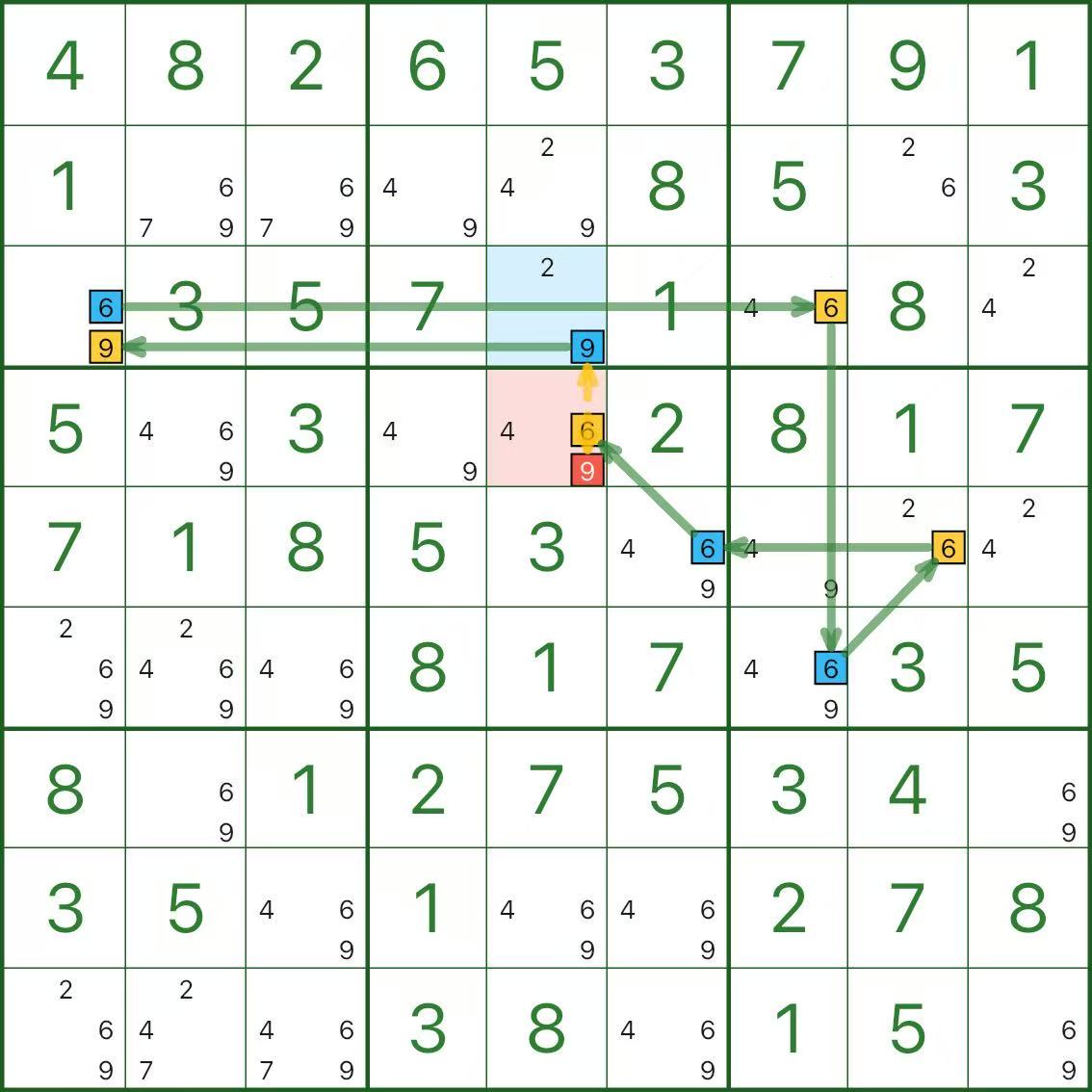
再看上图：红色要删除的是 r4c5 中的候选数字 9。
为什么能删？抓住“蓝黄必有一种为真”就够了：

• 如果蓝色为真：蓝色的 r3c5 中候选数字 9 就为真；而红色的 r4c5 中候选数字 9 与它冲突，所以红色不可能为真。
• 如果蓝色为假：同一条染色链里黄色就会为真；黄色的 r4c5 中候选数字 6 为真时，同一格里不可能同时填 6 和 9，所以红色的 r4c5 中候选数字 9 依然不可能为真。

无论哪种情况，红色候选都不能成立，所以可以删除。

---

同色冲突

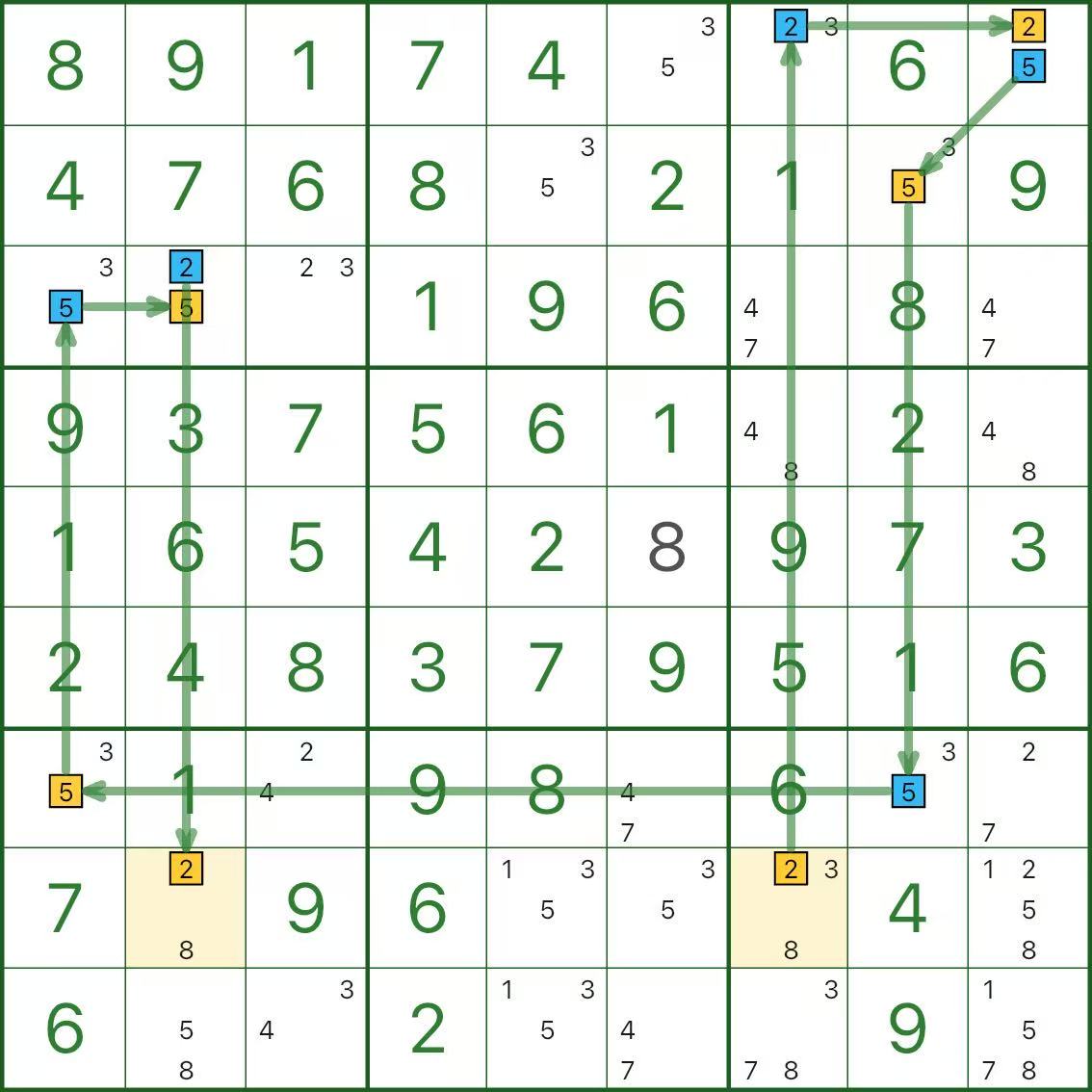
先看上图：在同一条染色链里，r8c2 和 r8c7 都出现了“黄色的候选数字 2”。
但它们同在第 8 行：同一行不可能出现两个 2 —— 这就是“同色冲突”。

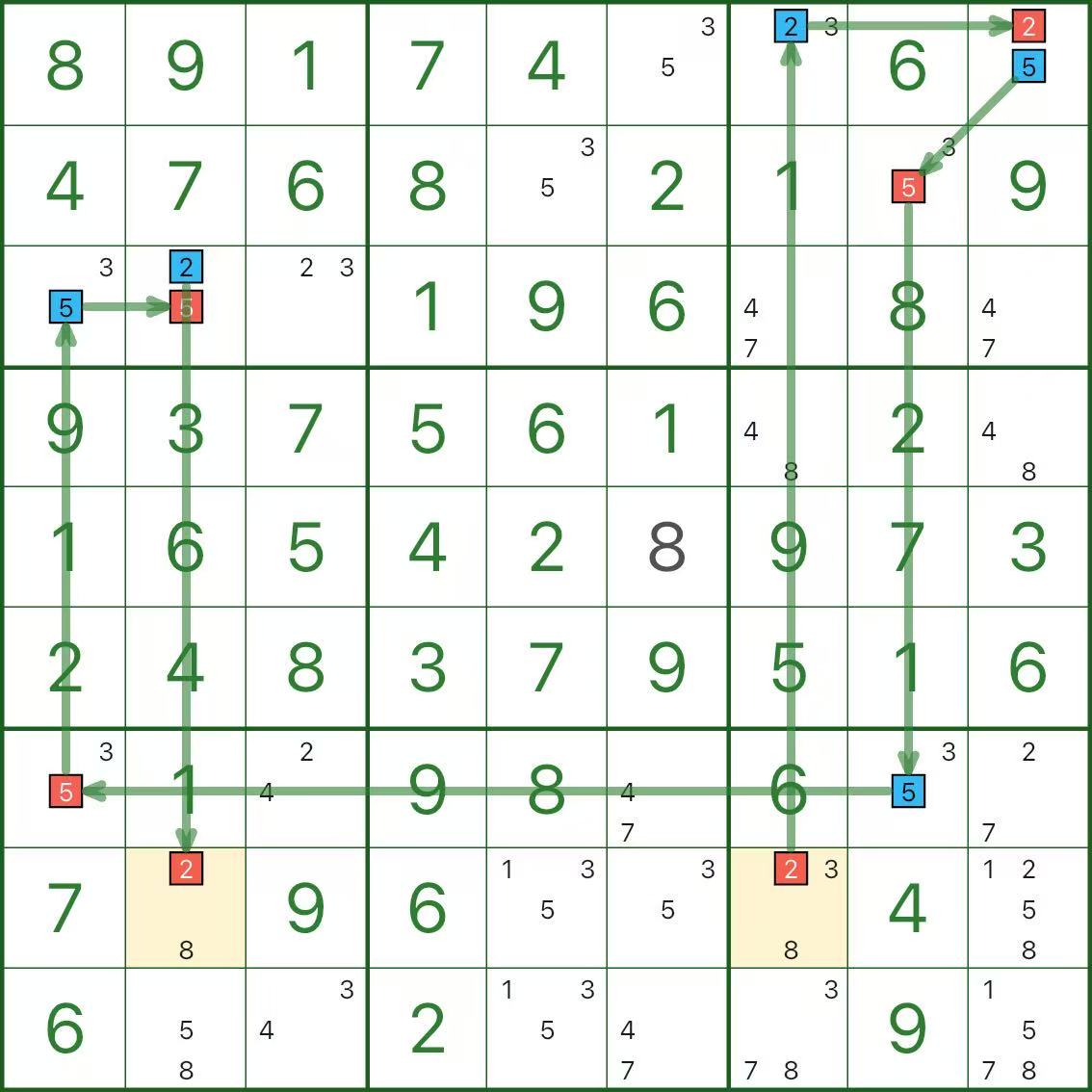
这说明：如果你假设“黄色为真”，就会立刻产生矛盾，所以黄色这条推导路线不成立。
因此，整条黄色链上的候选数都可以删除（上图已经把它们标成红色）。

---

如何寻找 3D 美杜莎（进阶染色）？

一句话：用“共轭对 + 双值格”把候选数连成网，蓝黄染色后找陷阱或同色冲突。

在游戏里你可以按这个顺序找：

1. 先找强链来源：共轭对（某数字在某行/列/宫只剩 2 处）与双值格
2. 沿着强链把候选数染成蓝/黄两色（两色互斥）
3. 优先找两类删数结论：
   • 红色候选同时与蓝色链、黄色链都冲突 → 陷阱删数
   • 同一行/列/宫（或同一格）里出现两个同色候选 → 整链删除该颜色