BUG+1

前置知识：BUG+1 依赖“题目只有唯一解”。如果你还没看过“唯一解”的说明，建议先从这里开始：
唯一解

---

1. 描述

BUG+1 的全称是 BUG+1（全双值坟墓 +1）。

名字听起来有点吓人，但它说的其实只是一个很具体的盘面形态：

• 绝大多数空格都已经被删到只剩 2 个候选数（双值格）
• 只有一个格子“多出来一个候选”，变成 3 个候选数

这就是 “+1” 的意思。

为什么叫 BUG？

BUG = Bivalue Universal Grave（双值普遍坟墓 / 全双值坟墓）

之所以叫“坟墓”，是因为在这种结构里候选数几乎都成对出现，常规的删数/出数很容易卡住。

当盘面满足下面两点时，就进入了 BUG 的“对称结构”：

1. 所有未填格都是双值格（每格 2 个候选）
2. 对任意一个数字 d，在每个区域（行/列/宫）里，d 作为候选出现的位置数是偶数
   • 最常见是 2 次
   • 如果该区域里 d 已经被填定，那么候选数可能是 0 次，这也仍然是偶数

这种结构会很“对称”，通常会导致 两种完整填法（也就是多解）。

那 BUG+1 是什么？

BUG+1 就是“几乎是 BUG，但差一点”：

• 除了一个“例外格”以外，其它所有未填格都是双值格
• 例外格有 3 个候选（多出来 1 个）

而这一个“多出来的候选”，会打破 BUG 的偶数对称——它也就成了我们能直接出数的关键。

这时我们可以利用“唯一解”做一个反证：如果你选错了（选了那两个“偶数候选”），盘面就会回到 BUG 的对称结构，变成多解；但题目必须唯一解，所以只能选那个“+1”的候选。

于是，我们就能直接确定：例外格子里会有一个候选是“+1”的那个，它必须为真——可以直接出数。

---

2. 详解

第一步：找到“几乎全是双值”的局面（上图）

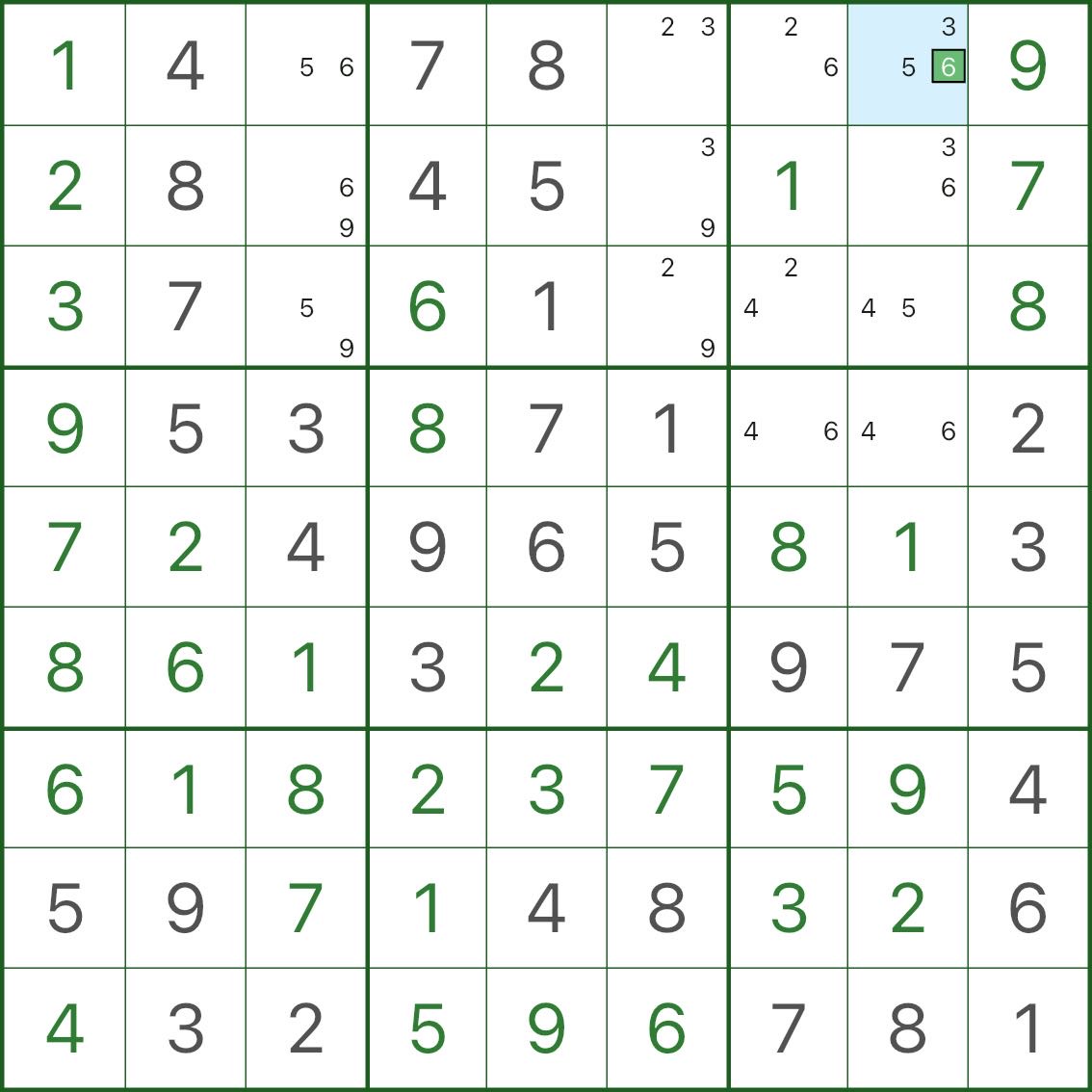
请先观察上图：

• 大部分空格的小数字都只剩 2 个候选
• 只有一个格子是“例外”，它有 3 个候选（也就是 BUG+1 的 “+1”）

第二步：这个格子到底填哪个数？（为什么是它）

思路很简单：我们只看这个例外格子里的 3 个候选数，并且只做一件事：数“偶数/奇数”。

做法是这样的：

1. 先看例外格子的 3 个候选分别是什么
2. 分别在它所在的 行 / 列 / 宫 里数一数：这三个数字各自作为候选出现了几次

你通常会看到：其中有一个数字在某个区域里出现了 3 次（奇数）。
这个“奇数候选”，就是我们要填入的那个数。

为什么是它？用反证最直观：

假设你不填这个“奇数候选”，而是去填另外两个“偶数候选”之一：

1. 例外格子会立刻变成双值格
2. 同时，盘面在行/列/宫里的候选数分布会重新变得“偶数对称”（回到 BUG 的结构）
3. BUG 的结构往往允许出现两种完整填法（多解）

但题目必须只有一个解，所以这种选择不可能成立。
因此：那个“奇数候选”必须为真——例外格子就应该填它。

如果你不想自己统计次数也没关系：在提示里，我们会把“要填的那个候选”用醒目的颜色标出来。

---

3. 例子

下图展示了 BUG+1 的结论：例外格子里那个“+1”的候选被直接确定并填入。

---

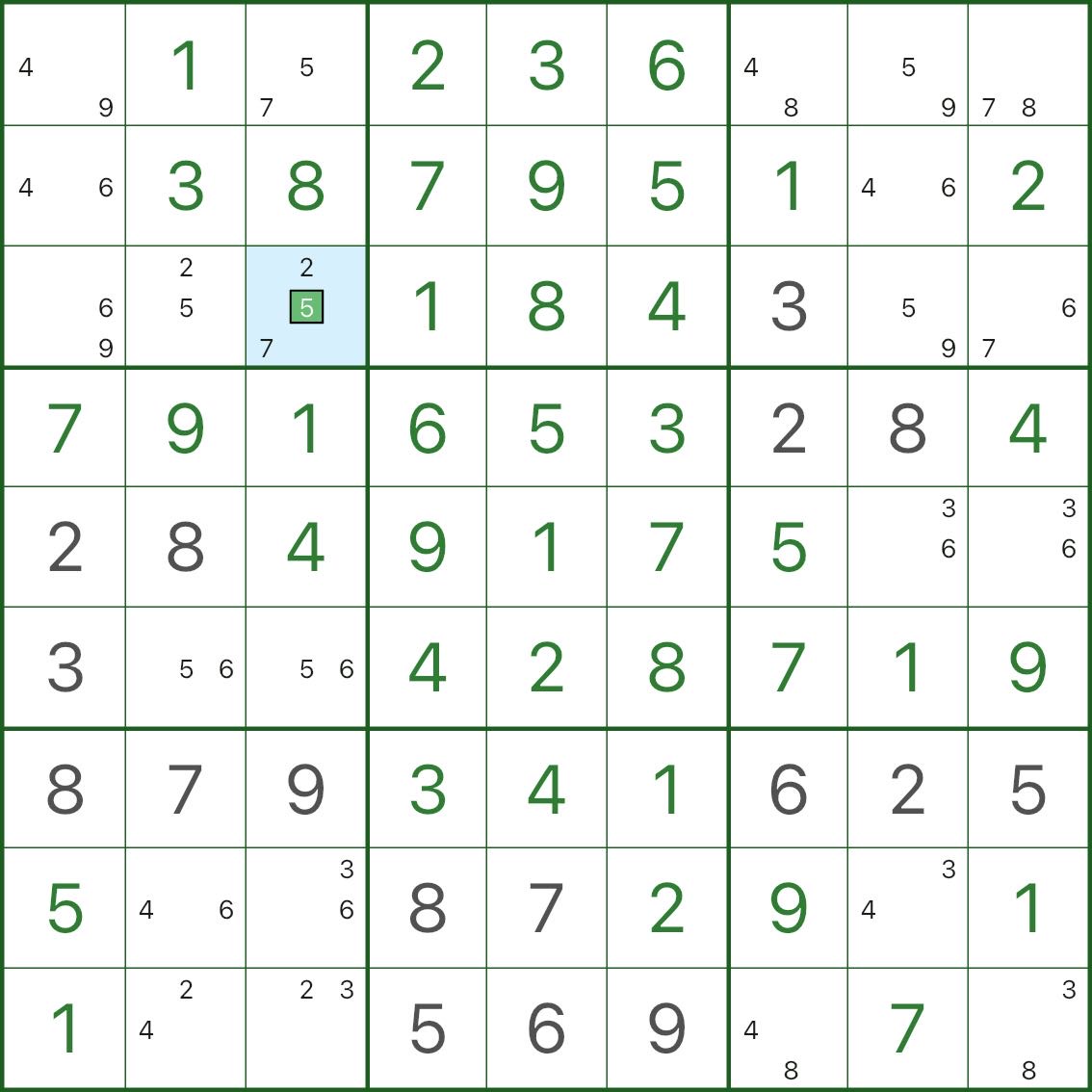
4. 如何寻找 BUG+1？

你可以按这个顺序检查：

1. 先确保候选数是完整、可靠的（必要时先补全候选数）
2. 看棋盘上未填格子里，是否出现：
   • 除了一个格子外，其余全部都是“双值格”
   • 那个例外格子是“三值格”（或少见的更多候选，但我们目前只讲最常见的 3 候选）
3. 在例外格子的行/列/宫里数一数这 3 个数字的候选次数：奇数（通常 3 次）那个就是要填的
4. 在提示里，例外格子会被标出来，并给出“必须填入的那个候选”

小提醒：BUG+1 是“唯一性推理”，只有在题目保证唯一解时才成立。