WXYZ翼

如果你已經看過這兩篇，會更容易理解 WXYZ翼：
XY翼 / XYZ翼

---

1. 描述

WXYZ翼可以理解為 XY翼/XYZ翼 的“加大版”：還是用一個小結構，把某個候選逼到矛盾，從而刪數。

它通常表現為一小團彩色格子（藍色樞紐格 + 黃色翼）：

• 這團結構裏所有候選數加起來，只涉及 4 個數字（比如 {1,4,7,9}）
• 如果我們假設某個紅色候選 d 為真，它會把結構裏其它位置的 d 都排除掉
• 結構裏就只剩 3 個數字要填進 4 個格子
  • ⇒ 必然有格子“無數可填”（矛盾）

所以紅色候選 d 可以刪除。

---

2. 詳解

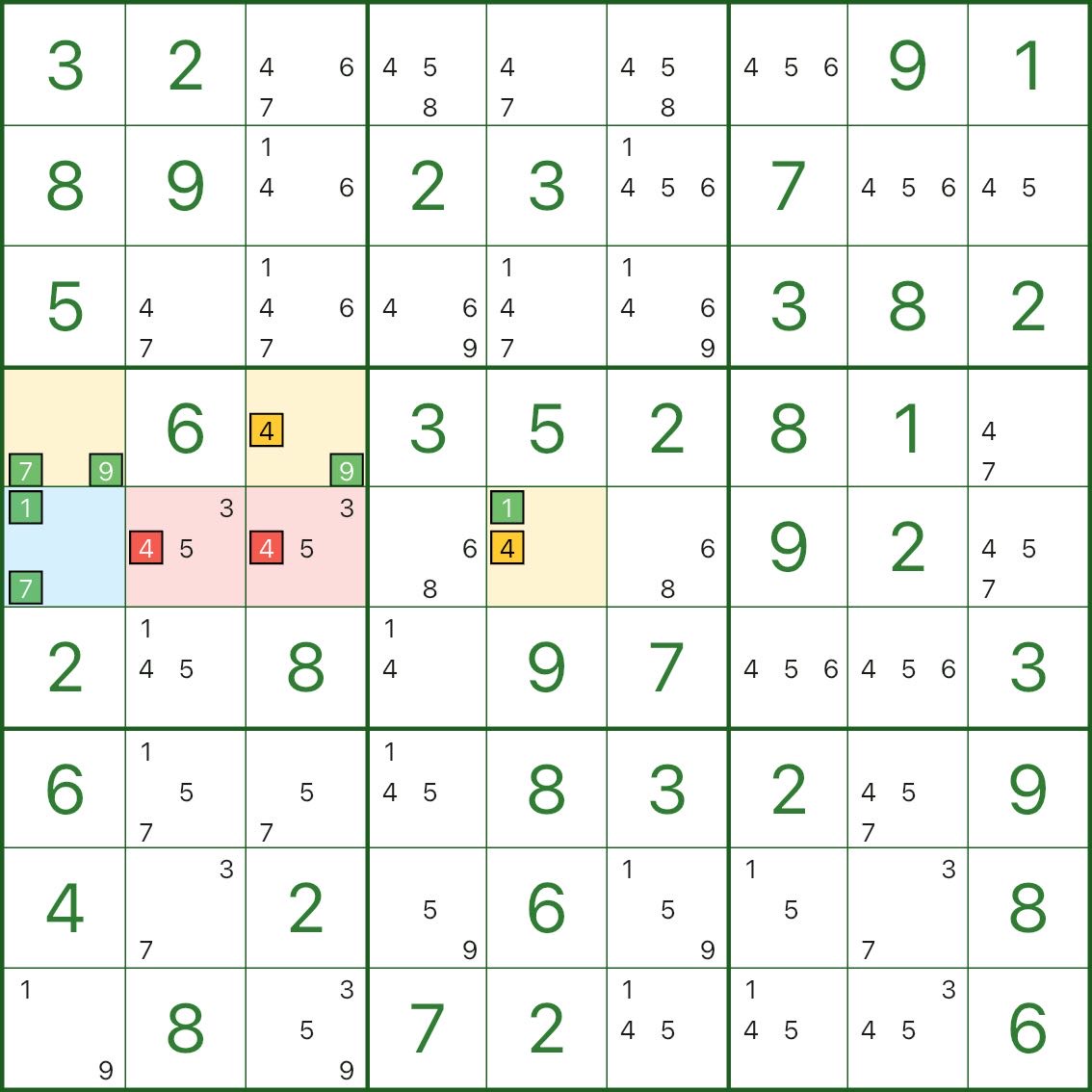
先看上圖：藍色是樞紐格，黃色是翼，紅色是刪數格。要刪除的是紅色格子裏的候選數字 4（r4c2、r4c3）。

為什麼紅色的 4 能刪？看一個很短的反證就夠了：

• 假設紅色格子裏 4 為真
• 這樣一來，黃色翼中與它衝突的 4 都會被排除
• 黃色翼就會被迫只能在 1、7、9 之間分配（上圖中已經用綠色候選數標出了這些數字）
• 但藍色樞紐格本來也只剩 1、7 這些候選
  當翼被迫佔用/封鎖了 1、7、9，樞紐格就會變成 無數可填（矛盾）

所以假設不成立：紅色格子裏的候選數字 4 可以刪除。

---

3. 例子

下面兩張圖是其它 WXYZ翼 的例子，你可以直接對照“藍色樞紐格 / 黃色翼 / 紅色刪數格”的結構來觀察：

---

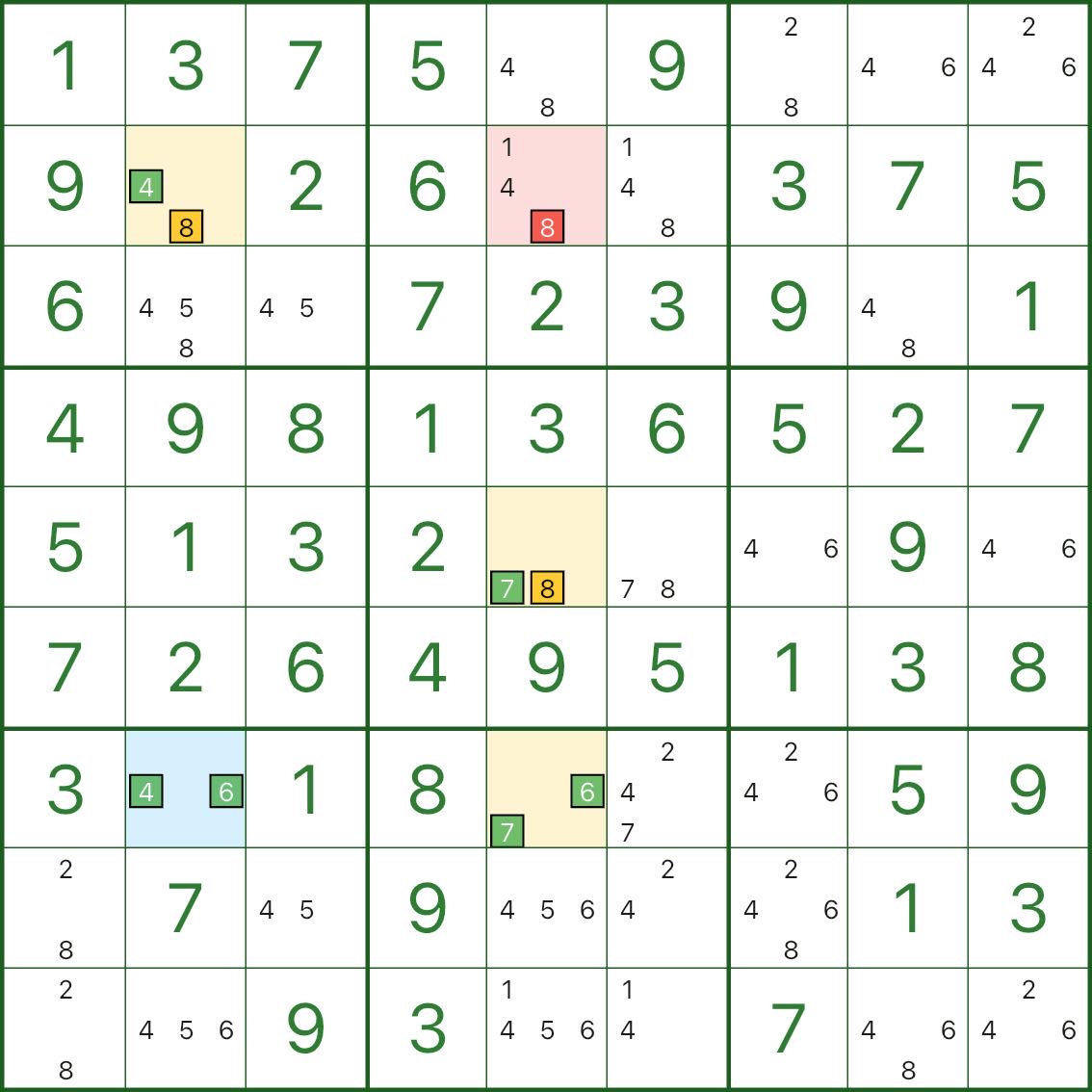
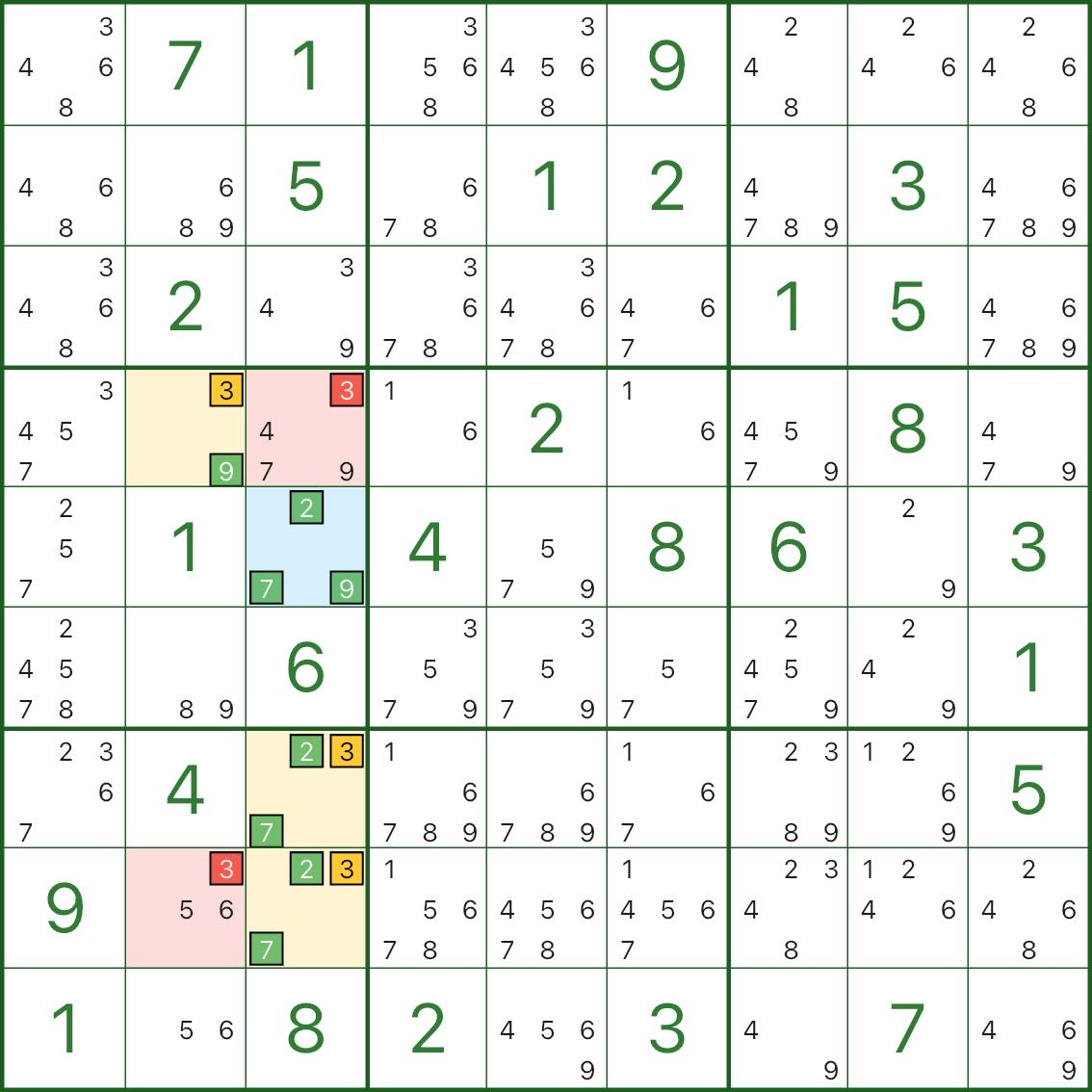
4. 如何尋找 WXYZ翼？

一句話：先找到一團藍黃結構只涉及 4 個數字，再從紅色候選出發做一次反證——如果它為真會讓藍黃結構裏出現“無數可填”，那它就能刪除。

在遊戲裏你可以按這個順序找：

1. 先留意一團相鄰或互相可見的彩色結構（藍色 + 黃色）
2. 看看它們的候選數加起來，是不是隻落在 4 個數字裏
3. 再看紅色刪數點：假設它為真時，結構中某個數字會被“擠掉”，最終導致結構裏至少有一個格子無數可填
4. 矛盾成立就可以刪數