W翼

描述

W翼是一種“刪候選”的短鏈技巧：它通常從 兩個相同的雙值格開始（我們也把它們叫作兩翼）。

它的核心直覺是：

• 兩翼裏都只有同一對候選數（例如 {a、b}）
• 如果某個格子的候選 b 為真，會把兩翼裏的 b 都排除掉
• 兩翼就會被迫都變成 a，從而在某個行/列/宮裏製造矛盾

所以這個格子裏的候選 b 就可以刪除。

---

詳解

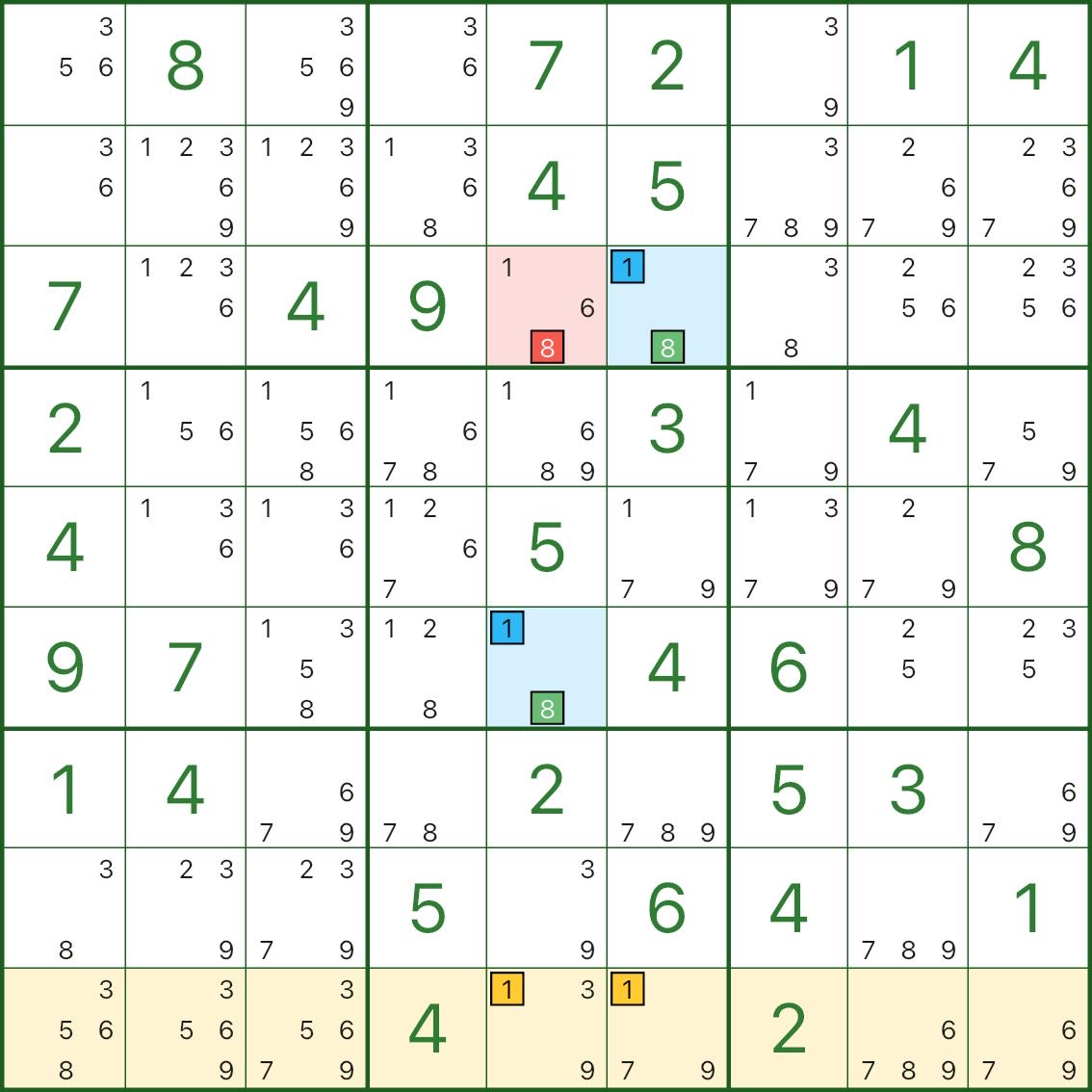
先看上圖：要刪除的是 r3c5 裏的候選數字 8（紅色）。
兩翼是 r3c6 與 r6c5，它們都是雙值格，候選數都是 1、8。
圖中黃色高亮的是 第 9 行，用來表示“如果兩翼都變成 1，會讓這一行裏 1 沒地方可填”。

為什麼 r3c5 中的 8 能刪？看一個很短的反證就夠了：

• 假設 r3c5 = 8（紅色候選為真）
• r3c5 能看見兩翼，所以兩翼裏的 8 都會被排除：
  • r3c6 只能變成 1
  • r6c5 只能變成 1
• 於是第 9 行會被“堵死”：黃色高亮的第 9 行裏，數字 1 的所有位置都會與這兩翼衝突，導致 第 9 行沒有 1 可填（矛盾）

所以假設不成立：r3c5 不能是 8，候選數字 8 可以刪除。

---

例子

下面三張圖是其他 W翼 的例子，你可以直接對照“兩翼 / 刪數點 / 矛盾行列宮”的結構來觀察：

---

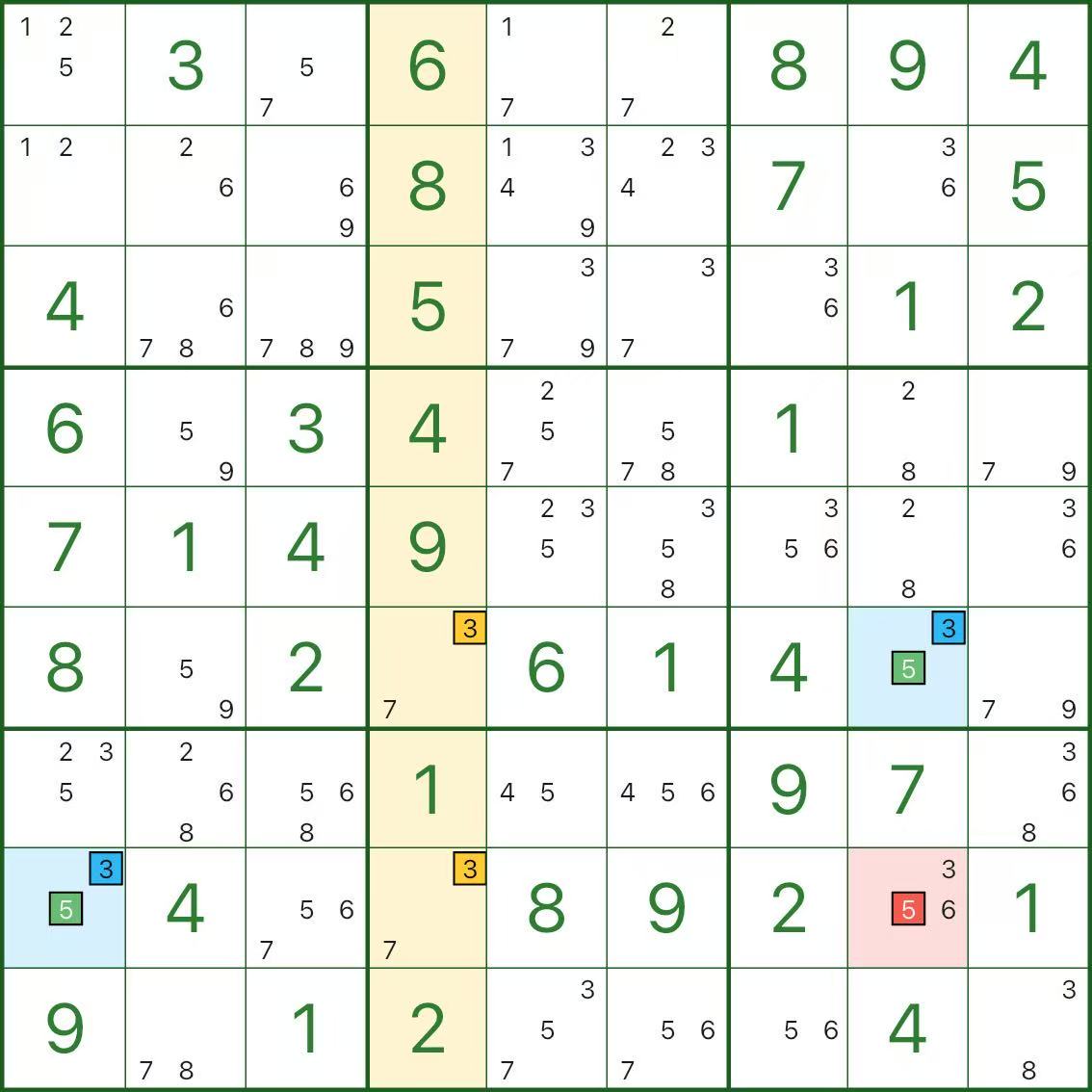
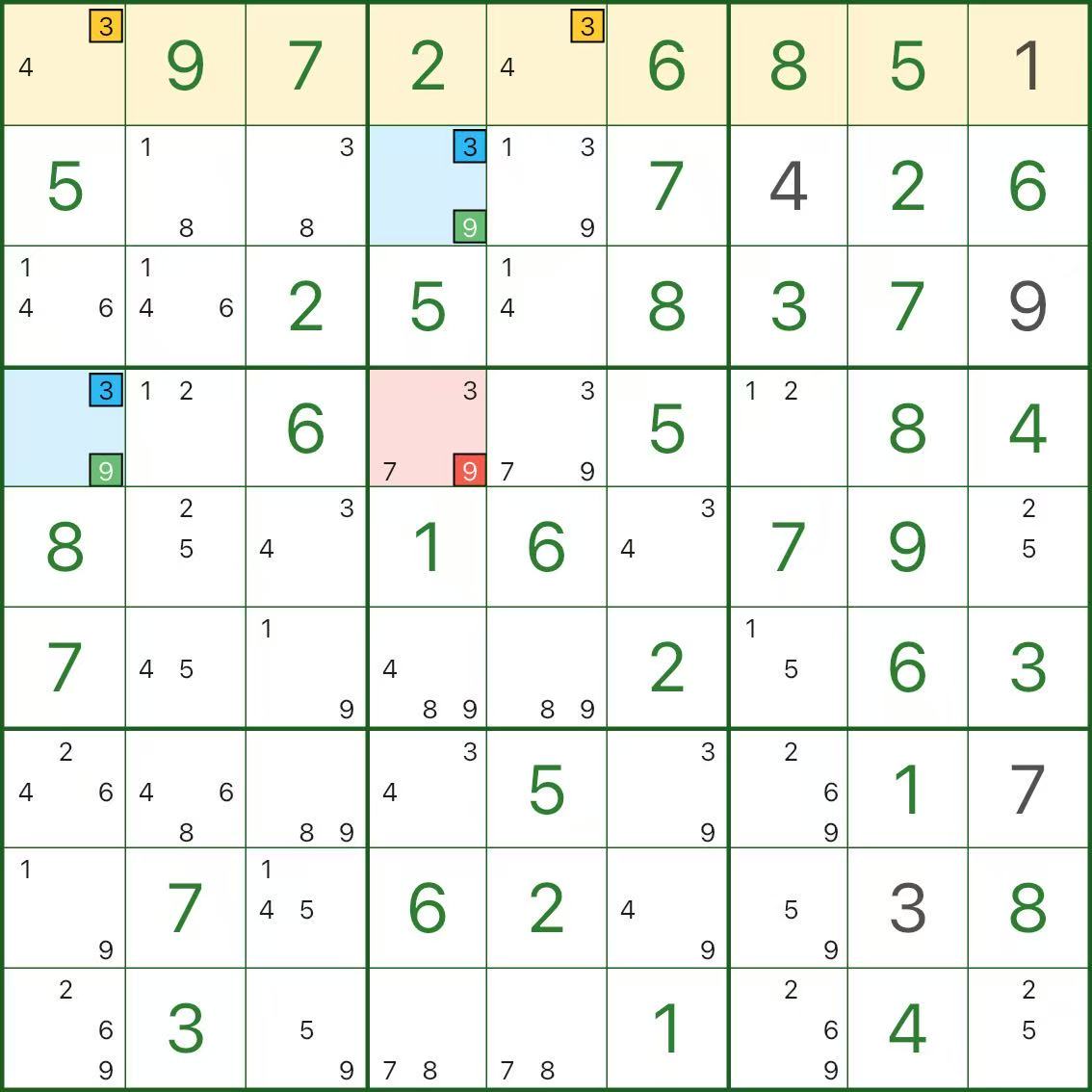
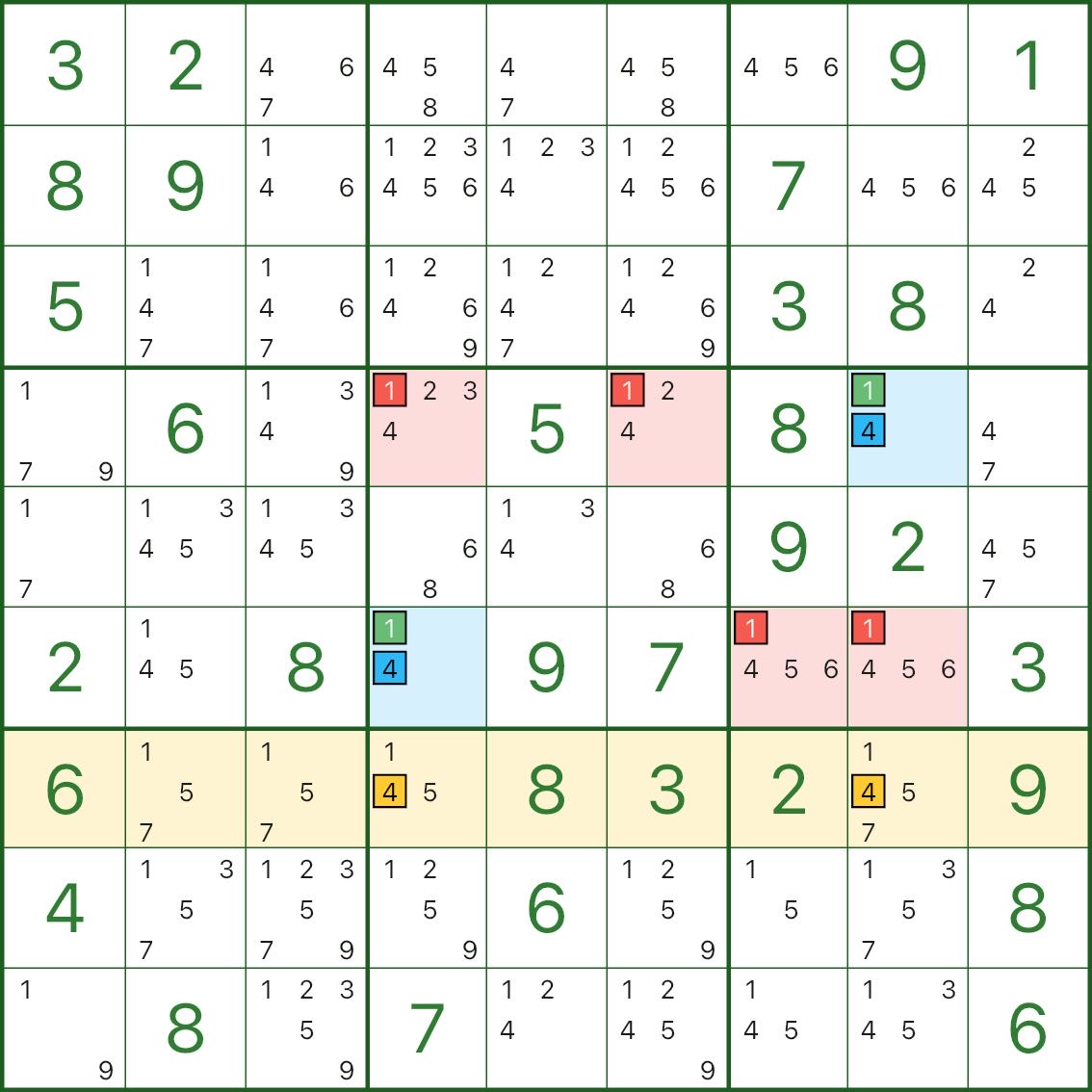
如何尋找 W翼？

一句話：先找兩格相同的雙候選當兩翼，再找一個能同時看見兩翼的刪數點，最後確認“兩翼被迫同取某數”會製造矛盾。

在遊戲裏你可以按這個順序找：

1. 先找兩個雙值格，它們的候選數完全相同（兩翼）
2. 找到一個格子能同時看見兩翼，並且它包含兩翼中的某個候選（常見就是要刪除的候選）
3. 做一次快速反證：假設這個候選為真 → 兩翼被迫同取另一個數字 → 在某個行/列/宮裏出現“該數字無處可放”的矛盾
4. 矛盾成立就可以刪數