BUG+1

前置知識：BUG+1 依賴“題目只有唯一解”。如果你還沒看過“唯一解”的説明，建議先從這裏開始：
唯一解

---

1. 描述

BUG+1 的全稱是 BUG+1（全雙值墳墓 +1）。

名字聽起來有點嚇人，但它説的其實只是一個很具體的盤面形態：

• 絕大多數空格都已經被刪到只剩 2 個候選數（雙值格）
• 只有一個格子“多出來一個候選”，變成 3 個候選數

這就是 “+1” 的意思。

為什麼叫 BUG？

BUG = Bivalue Universal Grave（雙值普遍墳墓 / 全雙值墳墓）

之所以叫“墳墓”，是因為在這種結構裏候選數幾乎都成對出現，常規的刪數/出數很容易卡住。

當盤面滿足下面兩點時，就進入了 BUG 的“對稱結構”：

1. 所有未填格都是雙值格（每格 2 個候選）
2. 對任意一個數字 d，在每個區域（行/列/宮）裏，d 作為候選出現的位置數是偶數
   • 最常見是 2 次
   • 如果該區域裏 d 已經被填定，那麼候選數可能是 0 次，這也仍然是偶數

這種結構會很“對稱”，通常會導致 兩種完整填法（也就是多解）。

那 BUG+1 是什麼？

BUG+1 就是“幾乎是 BUG，但差一點”：

• 除了一個“例外格”以外，其它所有未填格都是雙值格
• 例外格有 3 個候選（多出來 1 個）

而這一個“多出來的候選”，會打破 BUG 的偶數對稱——它也就成了我們能直接出數的關鍵。

這時我們可以利用“唯一解”做一個反證：如果你選錯了（選了那兩個“偶數候選”），盤面就會回到 BUG 的對稱結構，變成多解；但題目必須唯一解，所以只能選那個“+1”的候選。

於是，我們就能直接確定：例外格子裏會有一個候選是“+1”的那個，它必須為真——可以直接出數。

---

2. 詳解

第一步：找到“幾乎全是雙值”的局面（上圖）

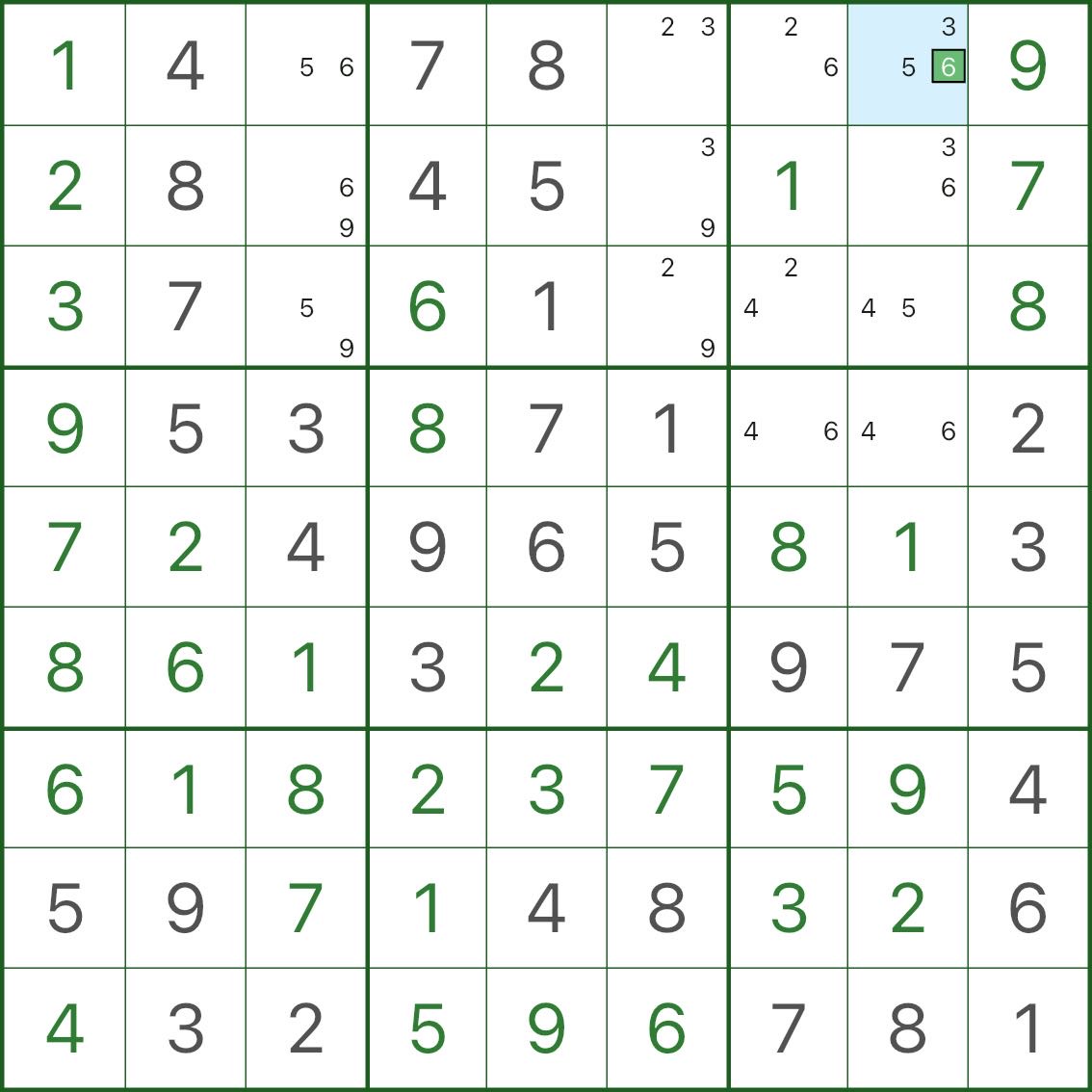
請先觀察上圖：

• 大部分空格的小數字都只剩 2 個候選
• 只有一個格子是“例外”，它有 3 個候選（也就是 BUG+1 的 “+1”）

第二步：這個格子到底填哪個數？（為什麼是它）

思路很簡單：我們只看這個例外格子裏的 3 個候選數，並且只做一件事：數“偶數/奇數”。

做法是這樣的：

1. 先看例外格子的 3 個候選分別是什麼
2. 分別在它所在的 行 / 列 / 宮 裏數一數：這三個數字各自作為候選出現了幾次

你通常會看到：其中有一個數字在某個區域裏出現了 3 次（奇數）。
這個“奇數候選”，就是我們要填入的那個數。

為什麼是它？用反證最直觀：

假設你不填這個“奇數候選”，而是去填另外兩個“偶數候選”之一：

1. 例外格子會立刻變成雙值格
2. 同時，盤面在行/列/宮裏的候選數分佈會重新變得“偶數對稱”（回到 BUG 的結構）
3. BUG 的結構往往允許出現兩種完整填法（多解）

但題目必須只有一個解，所以這種選擇不可能成立。
因此：那個“奇數候選”必須為真——例外格子就應該填它。

如果你不想自己統計次數也沒關係：在提示裏，我們會把“要填的那個候選”用醒目的顏色標出來。

---

3. 例子

下圖展示了 BUG+1 的結論：例外格子裏那個“+1”的候選被直接確定並填入。

---

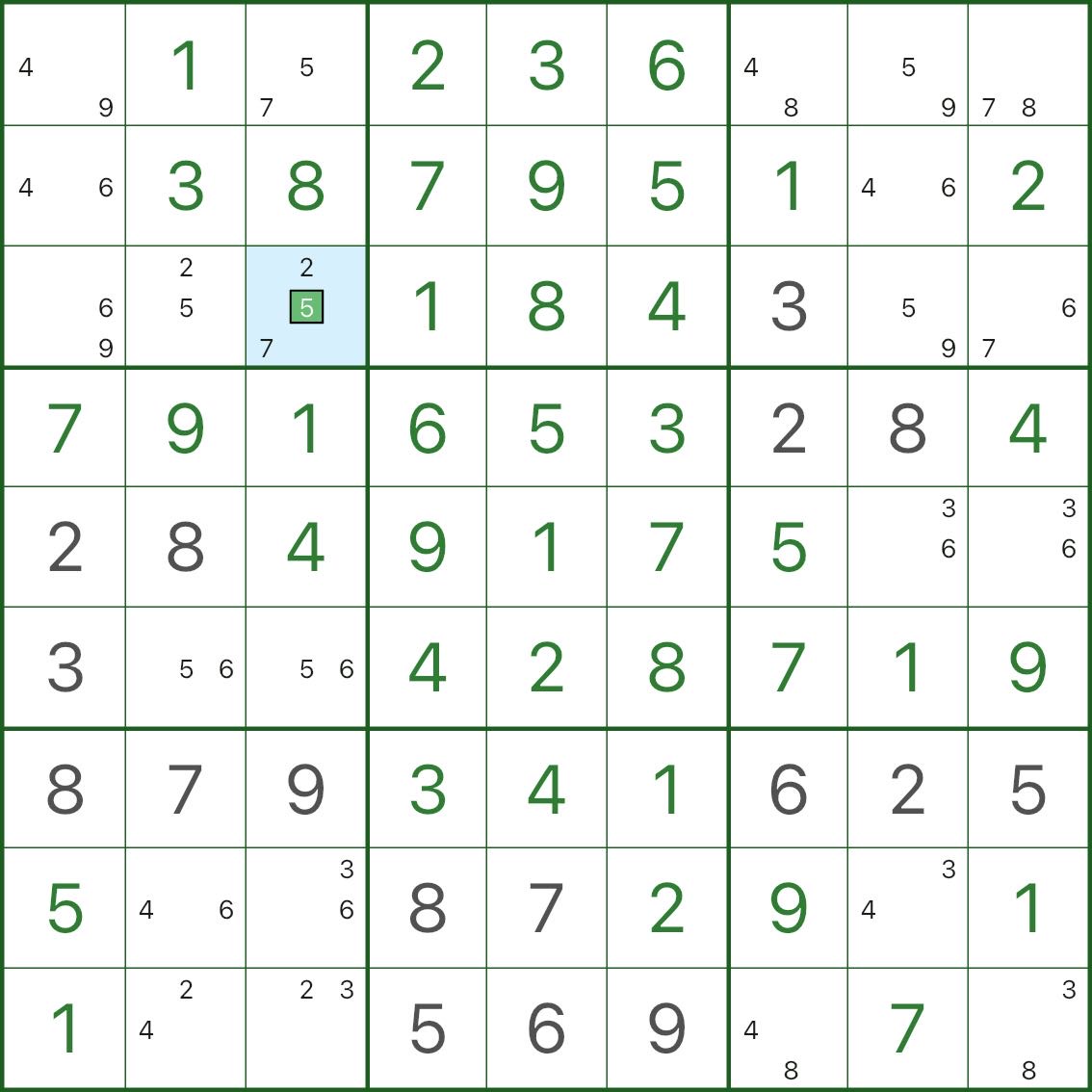
4. 如何尋找 BUG+1？

你可以按這個順序檢查：

1. 先確保候選數是完整、可靠的（必要時先補全候選數）
2. 看棋盤上未填格子裏，是否出現：
   • 除了一個格子外，其餘全部都是“雙值格”
   • 那個例外格子是“三值格”（或少見的更多候選，但我們目前只講最常見的 3 候選）
3. 在例外格子的行/列/宮裏數一數這 3 個數字的候選次數：奇數（通常 3 次）那個就是要填的
4. 在提示裏，例外格子會被標出來，並給出“必須填入的那個候選”

小提醒：BUG+1 是“唯一性推理”，只有在題目保證唯一解時才成立。