XY-крыло

Описание

XY-Wing (также известный как Y-Wing) — это короткая цепочка исключения кандидатов, состоящая из одного шарнира и двух крыльев.

Его форма выглядит следующим образом:

• Поворот (синий): ровно два кандидата x, y
• Крылья (желтые): {x, z} и {y, z}

Вывод: любая ячейка, которая видит оба крыла, не может содержать z, поэтому кандидата z можно исключить.

---

Объяснение

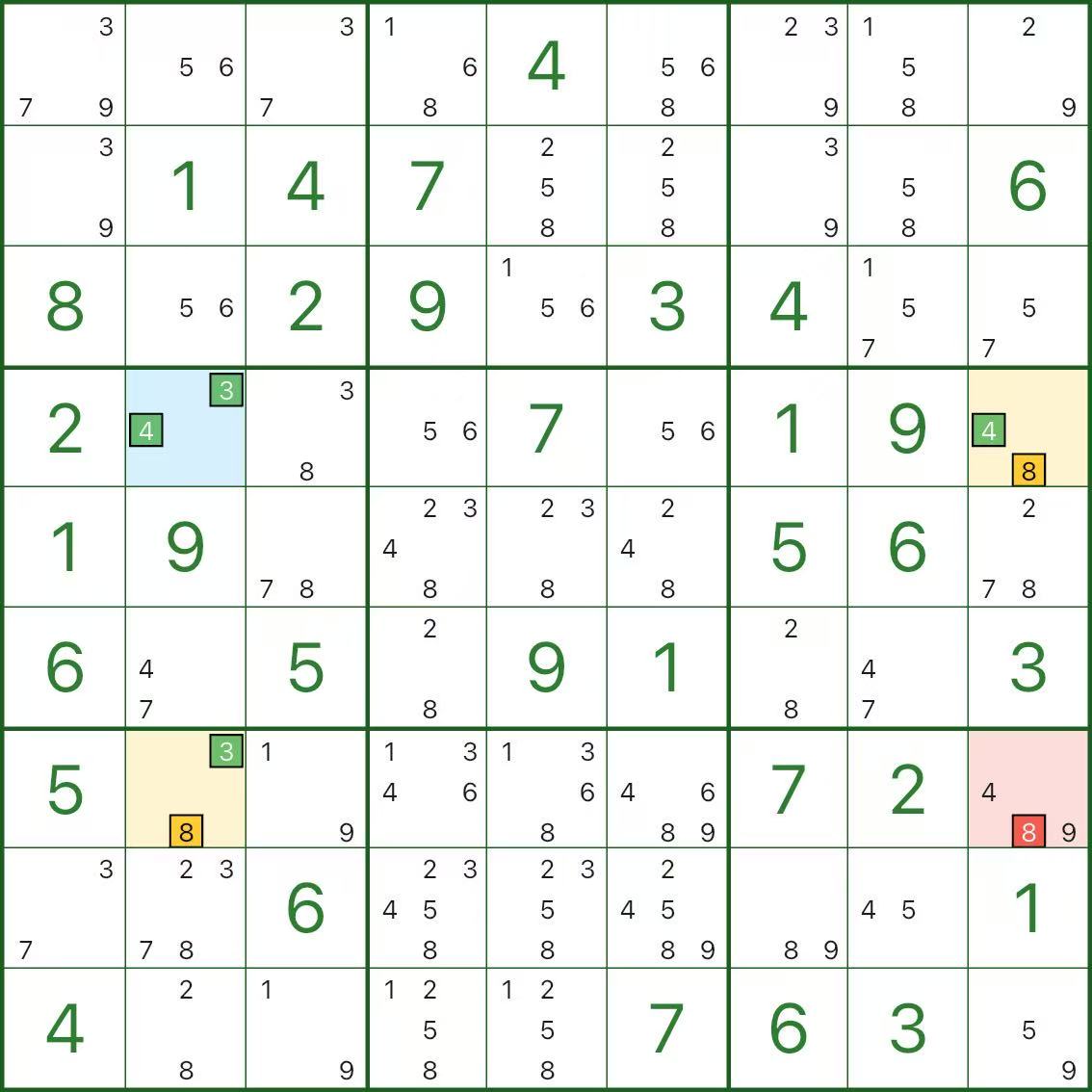
На изображении выше мы хотим исключить кандидата 8 в r7c9 (красный).
Синий центр — r4c2, с кандидатами 3 и 4.
Два желтых крыла:

• r4c9: кандидаты 4 и 8
• r7c2: кандидаты 3 и 8

Почему мы можем удалить 8 из r7c9? Достаточно короткого противоречия:

• Предположим, r7c9 = 8 (красный кандидат верен)
• r7c9 видит оба крыла, поэтому 8 удаляется из обоих крыльев:
  • r4c9 должно быть 4
  • r7c2 должно быть 3
• Теперь точка вращения r4c2 застряла:
  • r4c9 = 4 ⇒ r4c2 не может быть 4 (та же строка)
  • r7c2 = 3 ⇒ r4c2 не может быть 3 (тот же столбец)
  • в r4c2 было только {3,4} ⇒ значение не подходит (противоречие).

Таким образом, предположение невозможно: r7c9 не может быть 8, и кандидата 8 можно исключить.

---

Примеры

На этих изображениях показаны другие модели XY-Wing. Попробуйте обнаружить одну и ту же структуру: поворот (синий) / два крыла (желтый) / исключение (красный).

---

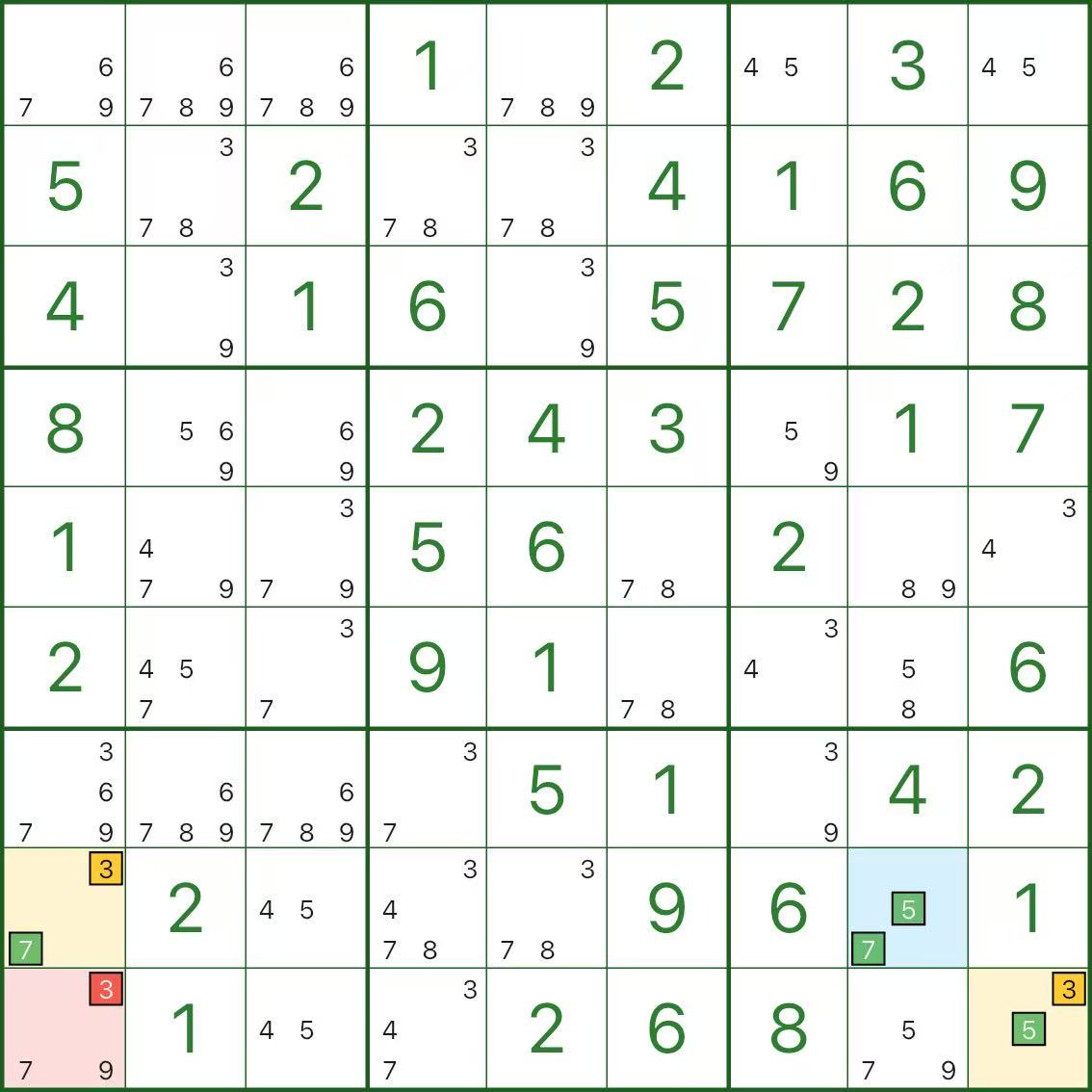
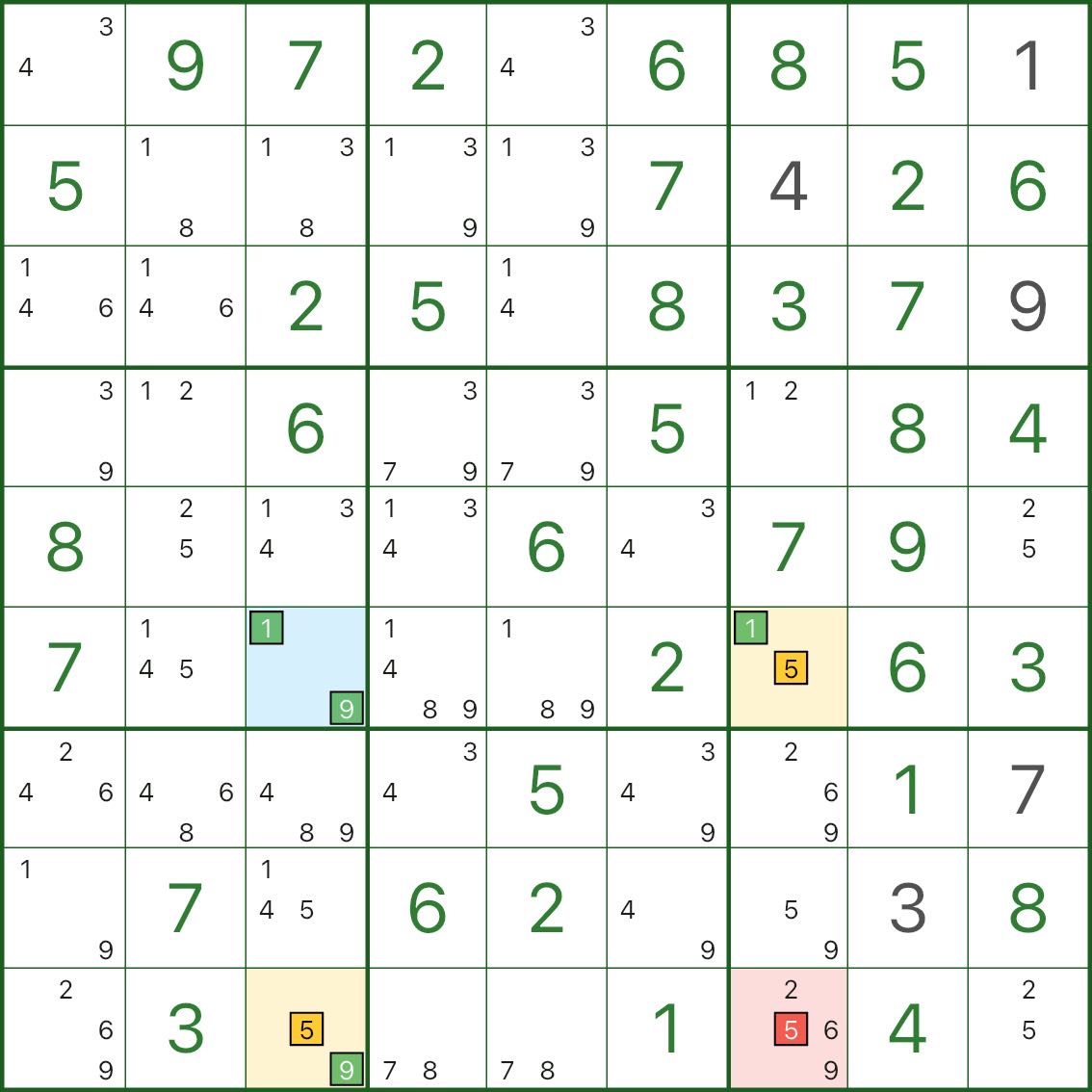
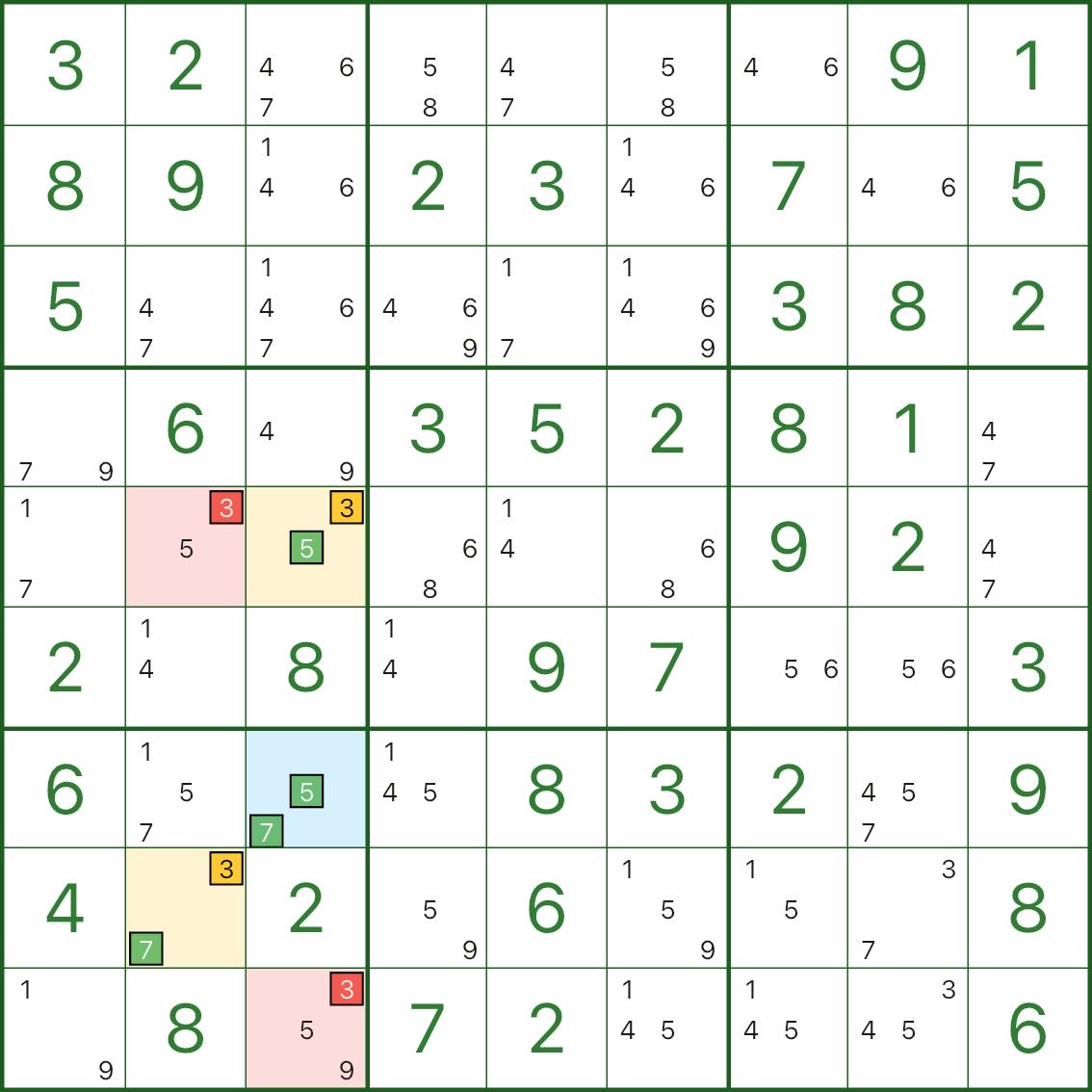
Как найти XY-крыло

Контрольный список в одну строку: найдите опорную точку с двумя кандидатами {x,y}, найдите два крыла с двумя кандидатами {x,z} и {y,z}, затем исключите z из любой ячейки, которая видит оба крыла.

В настоящей головоломке:

1. Найдите ячейку с ровно двумя кандидатами в качестве опорной (синяя).
2. Найдите две ячейки, которые могут видеть ось, каждая из которых содержит ровно два кандидата в форме {x,z} и {y,z} (желтый).
3. Любая ячейка, которая видит оба крыла, является типичной точкой исключения: удалите оттуда кандидата z (красный)