Уникальный прямоугольник (UR)

Предварительное условие: UR опирается на тот факт, что головоломка имеет ровно одно решение.
Если вы еще не читали, начните здесь:
Uniqueness

---

1. Обзор

Уникальный прямоугольник (UR) — это семейство методов, использующих свойство единственного решения для исключения кандидатов (а иногда и размещения числа).

Основное внимание уделяется «опасной форме»:

• четыре ячейки образуют прямоугольник 2×2 (две строки × два столбца, охватывающие ровно два поля)
• все четыре угла содержат одних и тех же двух основных кандидатов (например, 1 и 7)

Если мы оставим в этих четырех ячейках только эту пару, прямоугольник часто можно будет заполнить двумя разными способами (путем замены двух цифр), что нарушит уникальность.
Итак, исходя из предположения уникальности, мы можем сделать вывод: некоторые кандидаты должны быть удалены, или ячейка должна принять определенное значение.

---

2. Прохождение (5 типов)

Пять изображений ниже соответствуют пяти распространенным типам UR (подсказки в приложении обозначают их как типы I–V).

Руководство по цвету:

• Синие ячейки: прямоугольник UR (основная структура).
• Желтые отметки: кандидаты, на которых мы ориентируемся в рассуждениях.
• Красные метки: кандидаты на удаление / или ячейка, которую можно установить.

Тип I: одинарная крыша → принудительное значение

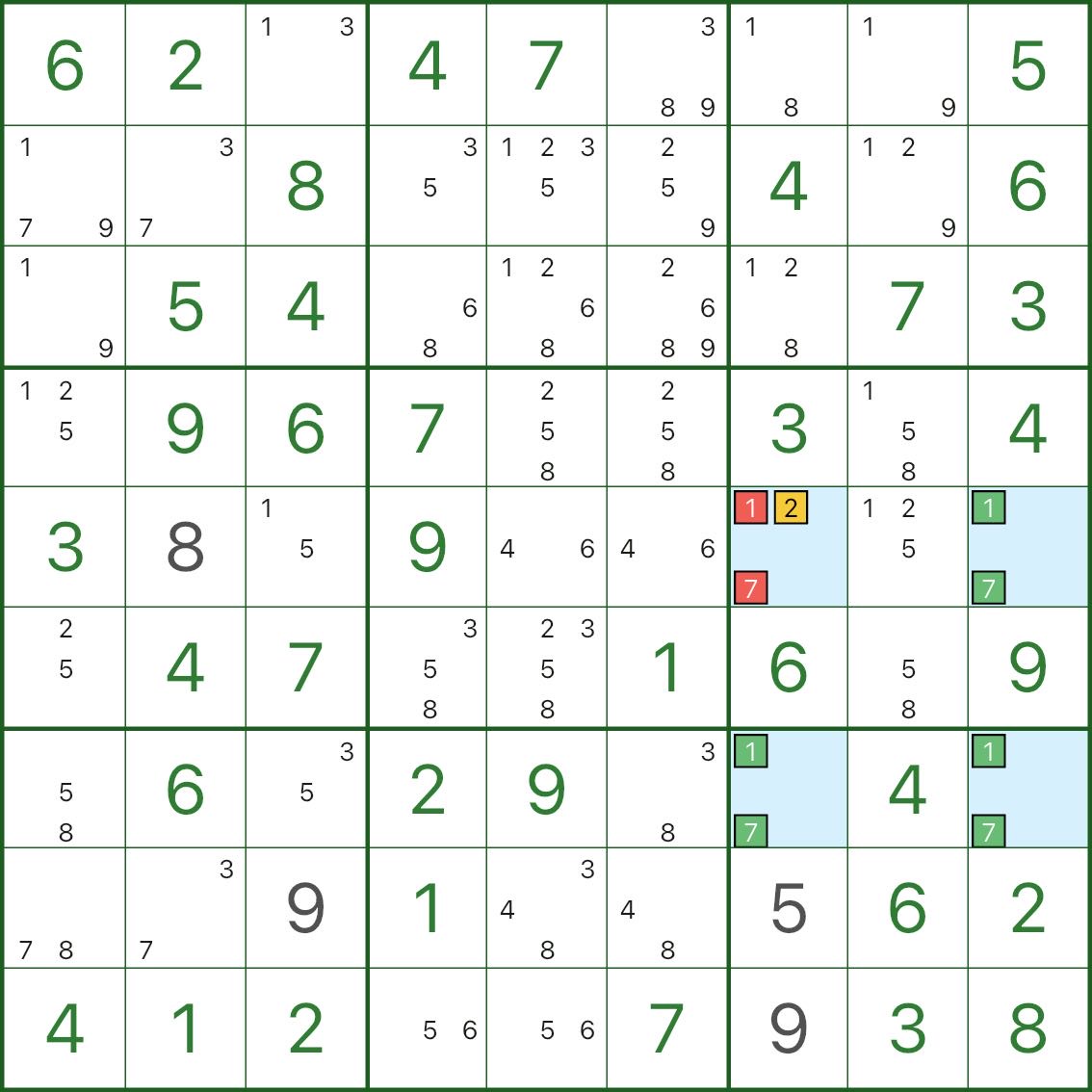
Посмотрите на четыре синие клетки: они образуют прямоугольник и все содержат кандидатов 1 и 7.
В ячейке r5c7 также есть дополнительный кандидат 2.

Если 2 неверно в r5c7, то в r5c7 останутся только 1 и 7.
Это сделает все четыре угла «только {1,7}», что позволит использовать две сменные заливки (нарушая уникальность).

Итак, по уникальности:

• r5c7 не может оставить кандидатов 1 и 7
• следовательно, r5c7 должно быть 2

---

Тип II: две крыши → исключить c, который видит обе крыши

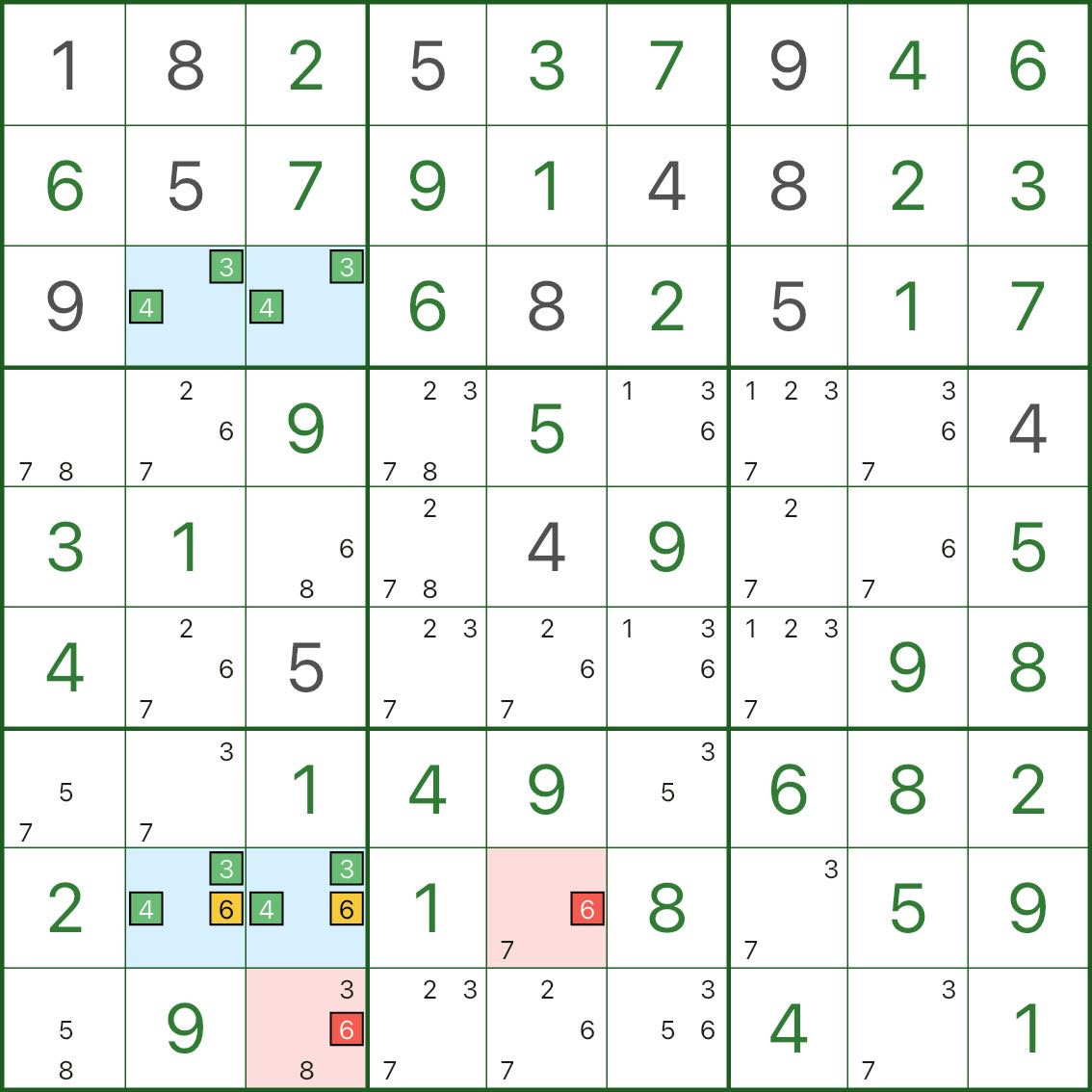
Здесь синий прямоугольник основан на основных кандидатах 3 и 4.
Две синие ячейки r8c2 и r8c3 также содержат кандидата 6 (то есть это {3,4,6}).

Теперь рассмотрим красного кандидата 6 (например, r8c5 или r9c3), который может видеть обе ячейки крыши:

• если бы эта красная 6 была правдой, обе крыши были бы взломаны а не 6
• крыши рухнут обратно только на {3,4}
• прямоугольник снова становится смертельным шаблоном {3,4} (нарушение уникальности)

Таким образом, эти красные 6 кандидатов не могут быть правдой и их можно исключить.

---

Тип III: рассматривать крыши как «пакет» и формировать подмножество

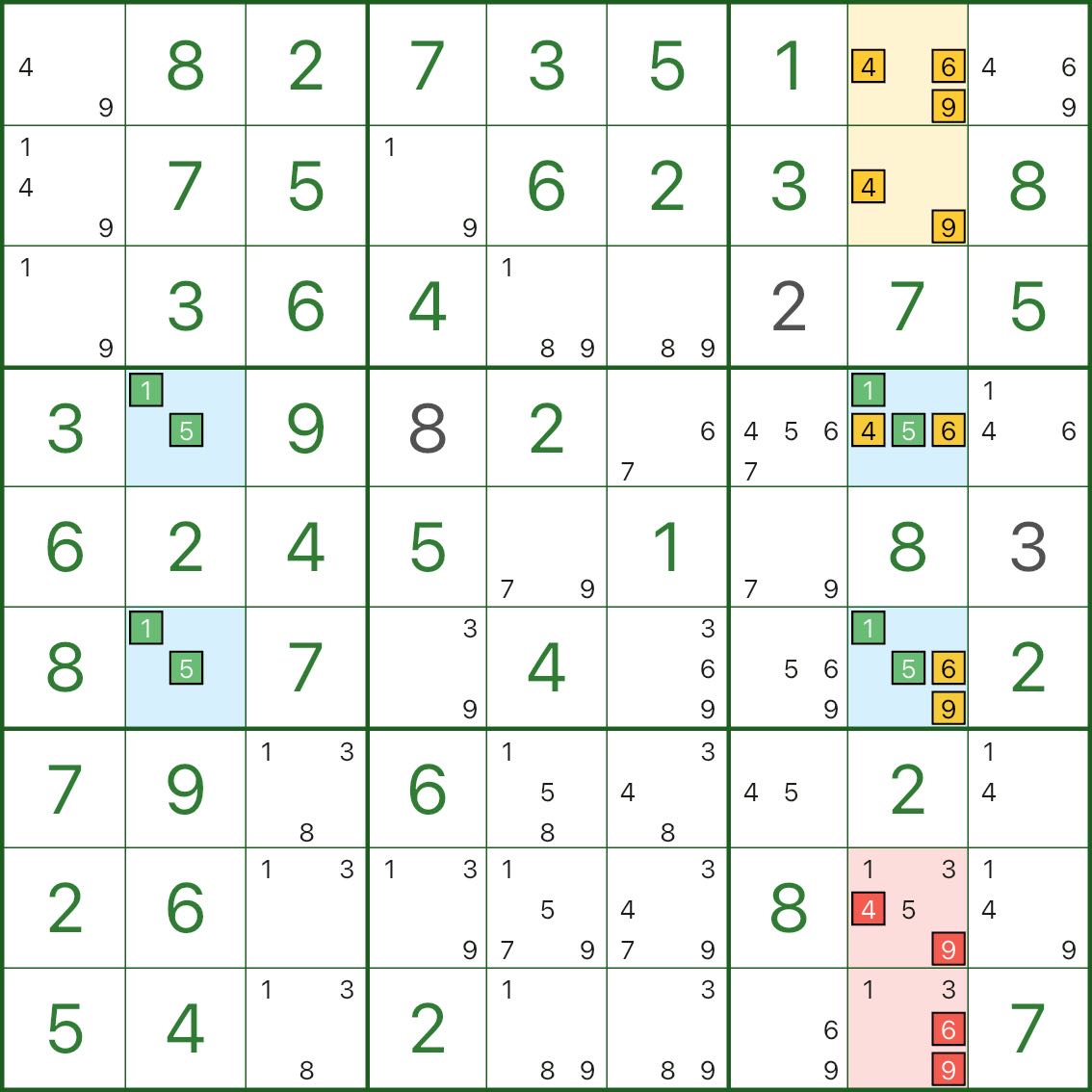
Здесь основное внимание уделяется столбцу 8:

• две синие ячейки в столбце 8 содержат кандидатов в ядро 1 и 5
• у них также есть общие дополнительные цифры 4, 6, 9 (то есть каждая из них равна {1,5,4,6,9})

Уникальность накладывает важное ограничение:

• среди этих двух синих ячеек хотя бы одна должна содержать цифру из {4,6,9}
• в противном случае оба будут полагаться только на {1,5}, превращая прямоугольник в смертельную модель.

Таким образом, мы можем рассматривать «дополнительные цифры {4,6,9} двух синих ячеек» как пакет.
Вместе с желтыми ячейками r1c8 и r2c8 это эффективно блокирует цифры 4, 6, 9 внутри небольшого подмножества в столбце 8.

Таким образом, любые другие кандидаты 4/6/9 в столбце 8 (отмечены красным) могут быть исключены.

---

Тип IV: сопряженная пара вызывает одну цифру → исключает другую

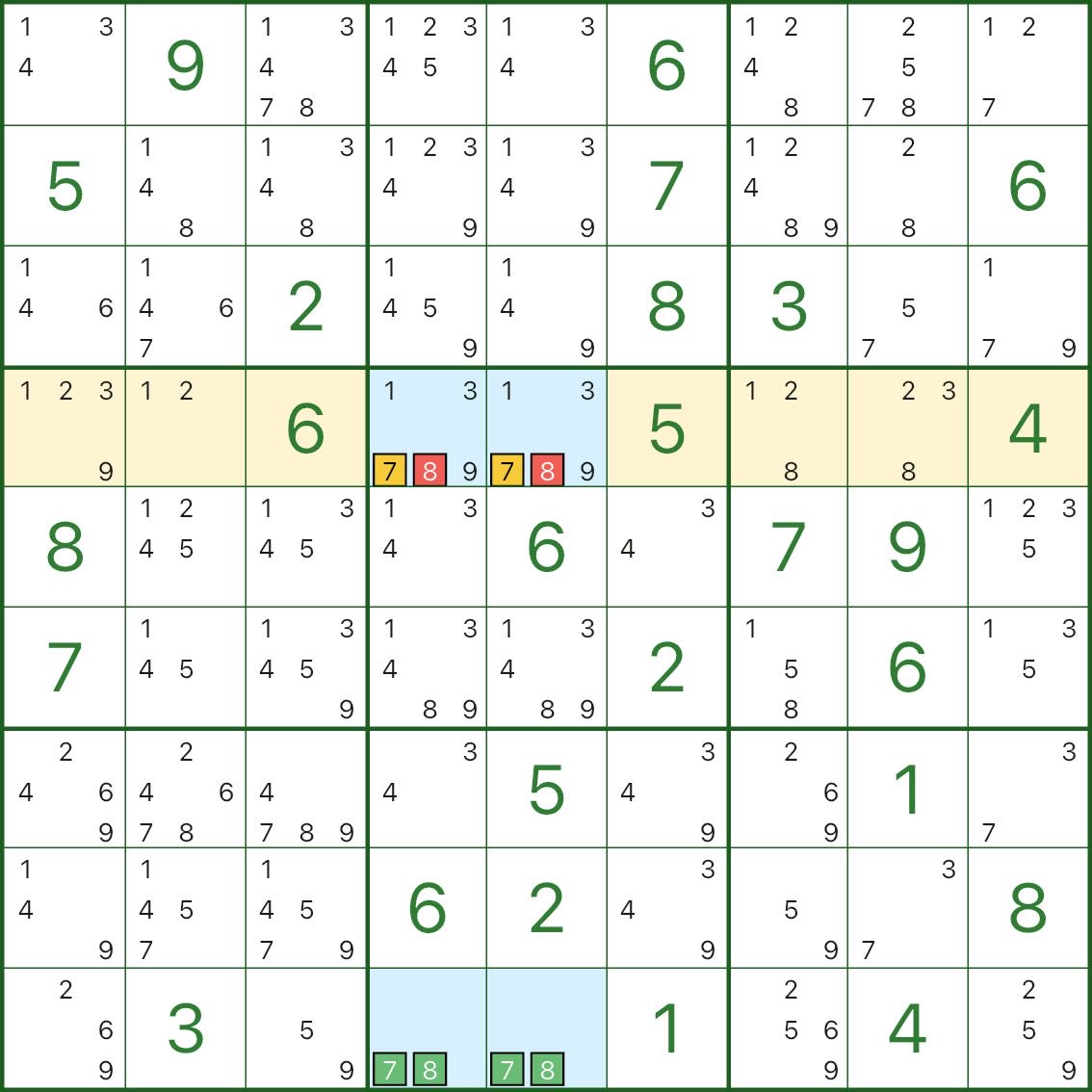
Синий прямоугольник снова построен на основе пары основных (здесь 7 и 8).В строке 4 кандидат 7 появляется только в двух синих ячейках r4c4 и r4c5.
Это означает:

• один из r4c4/r4c5 должен быть 7

При таком ограничении сохранение кандидата 8 в тех же синих ячейках все равно позволит прямоугольнику схлопнуться и превратиться в смертоносную структуру (нарушая уникальность).

Таким образом, мы можем исключить 8 из r4c4 и r4c5.

---

Тип V: несколько крыш (2 или 3) → исключить c, который видит все ячейки крыши

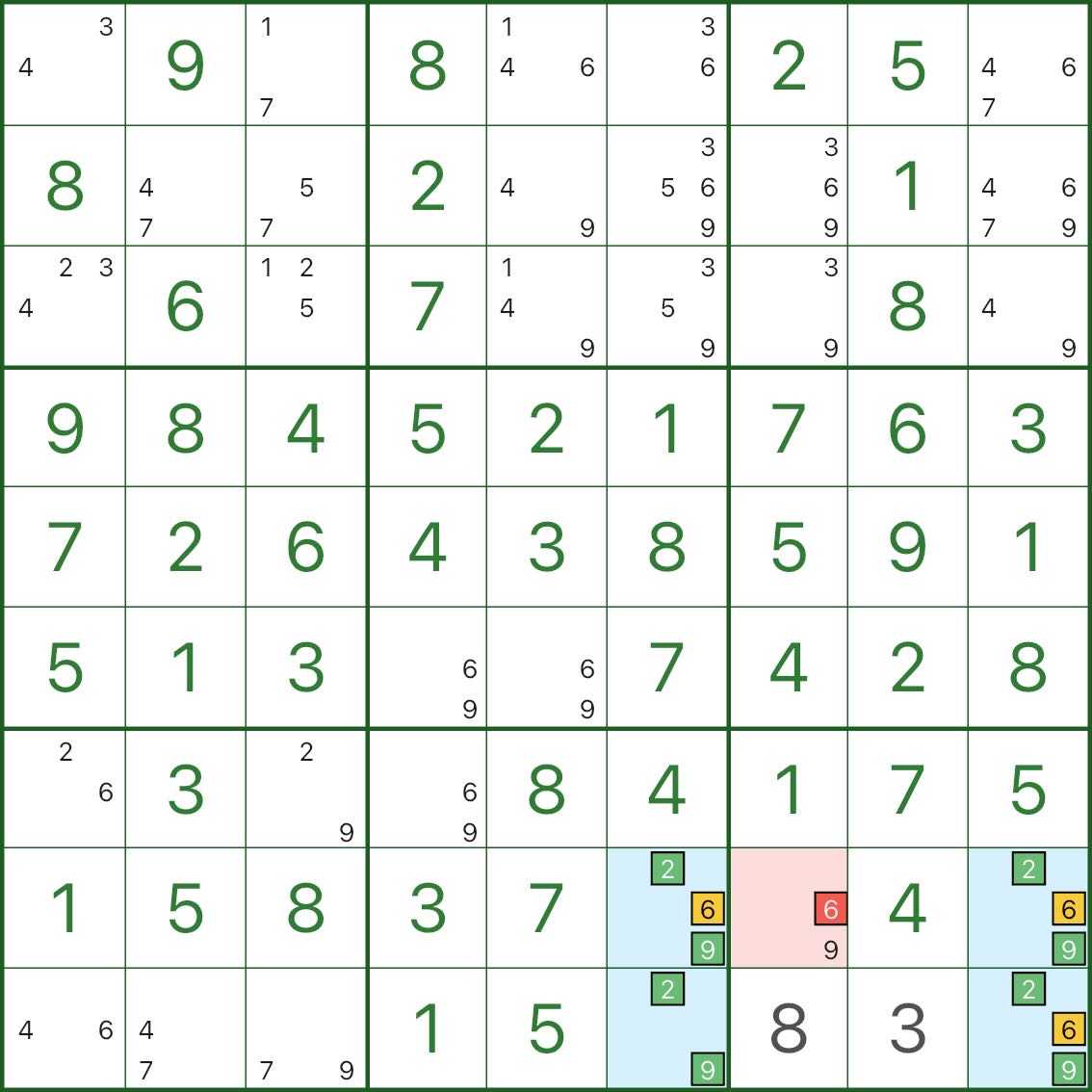
Тип V – это не строго «три крыши». Ключевая идея:

• в прямоугольнике 2 или 3 ячейки крыши, и все они имеют одного и того же дополнительного кандидата c
• если имеется только 2 ячейки крыши, они обычно не имеют одну и ту же строку/столбец/коробку (если они есть, это ближе к типу II)
• если кандидат ячейки c может видеть все эти ячейки крыши, то это c не может быть истинным и его можно исключить

На этом изображении синий прямоугольник состоит в основном из цифр 2, 6, 9:

— три синих угла — это {2,6,9}

• оставшийся синий угол равен {2,9} (отсутствует 6)

Теперь посмотрите на красную ячейку r8c7: у нее есть кандидат 6, и она может видеть все ячейки крыши {2,6,9} в этом шаблоне.

Если r8c7 = 6:

• все три ячейки крыши будут принудительно не-6
• они схлопнутся только в {2,9}
• прямоугольник становится смертельным шаблоном {2,9} (нарушая уникальность)

Таким образом, кандидат 6 в r8c7 не может быть истинным и его можно исключить.

---

3. Примеры

Изображения 1–5 в этой статье уже являются примерами типов I–V.
Во время практики постарайтесь сначала обнаружить синий прямоугольник, а затем сопоставить желтые/красные отметки с приведенными выше рассуждениями.

---

4. Как определить уникальный прямоугольник

В настоящих головоломках искать можно в таком порядке:

1. Найдите четыре пустые ячейки, которые образуют прямоугольник 2×2 (две строки × два столбца) и занимают ровно два поля.
2. Проверьте, все ли четыре угла имеют одних и тех же двух основных кандидатов («смертельная пара»).
3. Затем классифицируйте по тому, как выглядят лишние кандидаты:
   • только в одном углу есть лишние кандидаты → Тип I (часто принудительное значение)
   • два угла имеют одну и ту же дополнительную цифру c → Тип II
   • дополнительные цифры крыш могут образовывать подмножество в строке/столбце/блоке → Тип III
   • в доме одна основная цифра появляется только в двух прямоугольных клетках → Тип IV
   • два или три угла имеют одну и ту же дополнительную цифру c (для двух крыш они обычно не делят дом) → Тип V

Это UR в одном предложении: никогда не позволяйте прямоугольнику превратиться в смертельный узор — иначе уникальность будет нарушена.