Основы цепочки

Сильные звенья/слабые звенья/чередование (AIC)

Цепочки являются основным строительным блоком для многих продвинутых техник судоку.
По сути, цепочка — это просто последовательность выводов «если… то…», которая позволяет выводам перемещаться по сетке.

После этой главы расширенные подсказки, такие как однозначные цепочки, воздушный змей, небоскреб, медуза и AIC, станут гораздо более читабельными.

Мы используем r1c1 для обозначения позиции ячейки:
r = строка, c = столбец.

Чтобы облегчить понимание диаграмм, мы используем:

• Зеленая сплошная линия: сильная связь.
• Желтая пунктирная линия: слабое звено.
• Синий/желтый фон кандидата: два взаимоисключающих «состояния» для визуализации чередования.
• Красный кандидат: кандидат, которого нужно исключить на этом этапе.

Напоминание: цепочка двунаправленная. Стрелки предназначены только для удобства чтения.

---

Что такое цепочка?

Короче говоря, цепочка соединяет отношения-кандидаты, поэтому вы можете продолжать применять логику «если… то…»:

Если А невозможно, то Б должно быть истинным;
если B истинно, то C должно быть ложным;
…

Цепь состоит из:

• Узлы: кандидаты (цифра-кандидат в ячейке).
• Связи: отношения между кандидатами (сильные/слабые)

Цепочка не обязательно означает «мы всегда удаляем начало». Это больше похоже на путь рассуждения:

• Достигните противоречия ⇒ докажите, что кандидат не может быть правдой → устраните его.
• Достигните вынужденной истины ⇒ докажите, что кандидат правдив → установите значение

В данной статье основное внимание уделяется наиболее распространенным «однозначным цепочкам»: рассуждениям о кандидатах на одну цифру d.
(Отношения двузначных ячеек и сильные связи групп/регионов рассматриваются позже.)

---

Сильные и слабые ссылки

Сильная связь (сопряженная пара)

Мнемоника: или-или.

Если в одном и том же блоке (строке/столбце/блоке) цифра d появляется в ровно двух ячейках-кандидатах, эти два кандидата образуют сильную связь (сопряженную пару).

Ключевой вывод: «НЕ заставляет ДА»:

• Если НЕ А, то Б (Если А не d, то B должно быть d)
• Если НЕ Б, то А

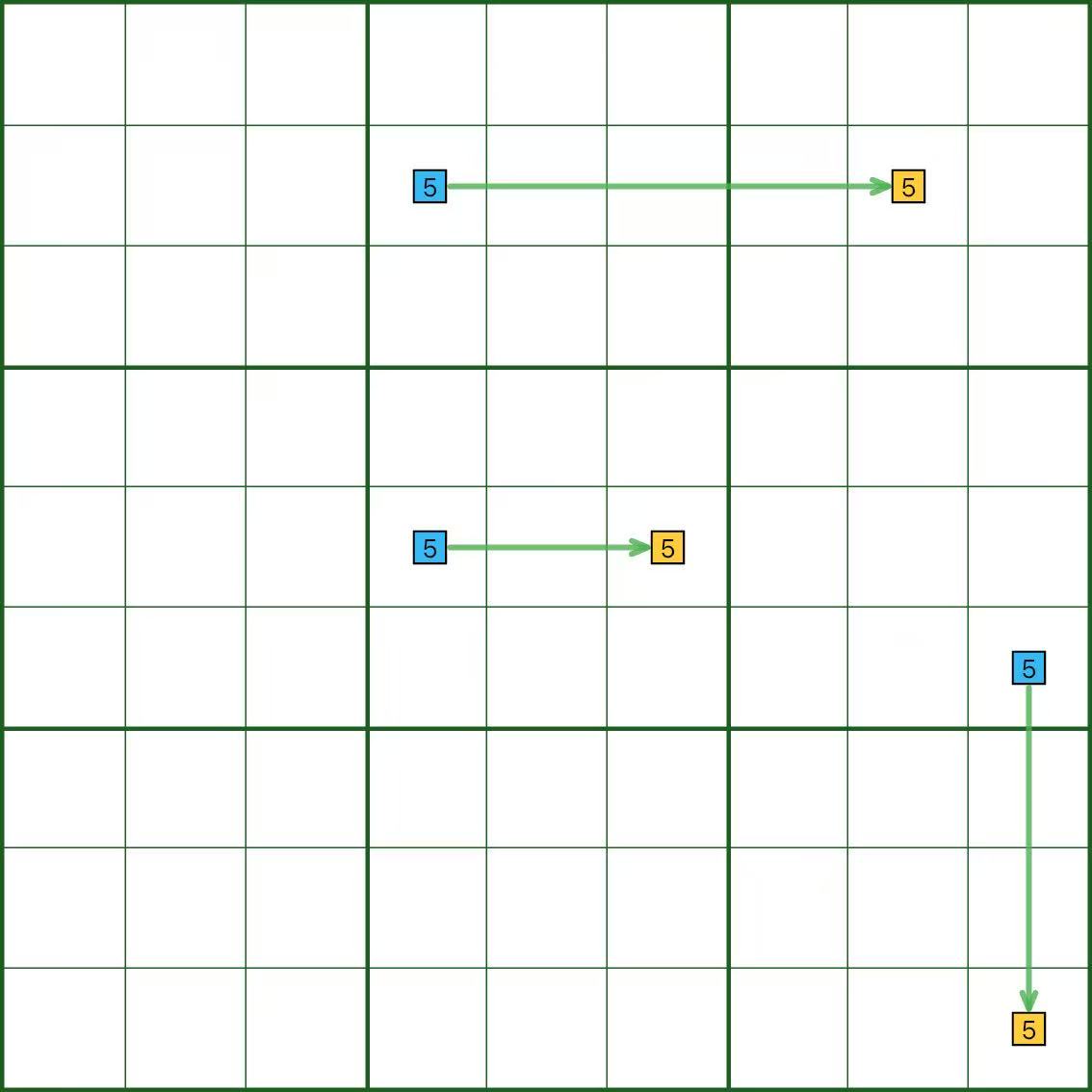
На диаграмме цифра 5 образует сильные связи в строке, столбце и блоке.
Вы можете читать его с любого конца; стрелки — это просто средство чтения.

Важное примечание: каждая сильная ссылка также является слабой.
Поскольку два кандидата используют одну и ту же единицу, они не могут оба быть истинными:

• Если A истинно, то B ложно (Если A есть d, то B не есть d)

Однострочное резюме:

Сильная ссылка = слабая эксклюзивность + «одно из них должно быть правдой»

Слабое звено

Мнемоника: если вы видите друг друга, вы оба не можете быть правдивыми.

Слабая ссылка выражает одну вещь:

Два кандидата не могут оба быть правдивыми.

В однозначных цепочках наиболее распространенным слабым звеном являются два кандидата одной и той же цифры d в одной единице.

Значение:

• Если А, то НЕ Б

Но не наоборот:

• Если А ложно, вы не можете сделать вывод Б (может быть третье место).

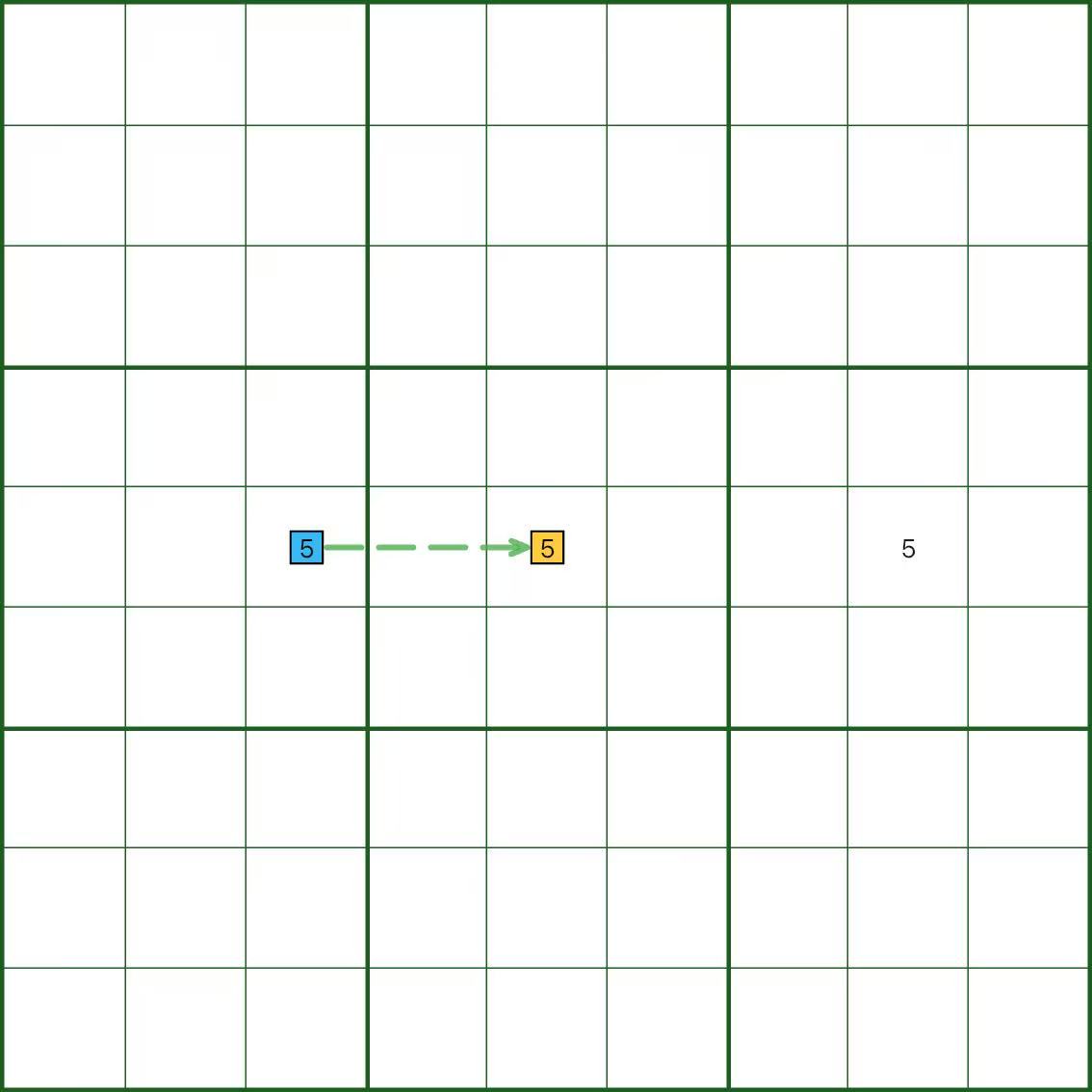
На диаграмме цифра 5 имеет три ячейки-кандидата подряд, поэтому каждая пара слабо связана.
На рисунке изображен только один пунктирный сегмент, чтобы показать, как выглядит слабое звено.

---

Как работают цепи?

Для распространения по цепочке запомните два правила:

1. Верно → (слабое) → Ложь
   Слабые связи являются исключительными: если A истинно, B должно быть ложным.
2. Ложно → (сильное) → Верно
   Сильные связи — это «или-или»: если A ложно, другой кандидат должен быть истинным.

Итак, рабочая цепочка обычно чередуется:

Ложно — (сильное) → Верно — (слабое) → Ложно — (сильное) → Верно — (слабое) → Ложь …

Зачем чередовать?

• слабые-слабые разрывы: «ложь» не распространяется через слабое звено.
• сильный-сильный может соединяться, но во многих головоломках это часто соответствует более простым закономерностям, поэтому цепочки наиболее полезны для поочередного распространения

---

Пример

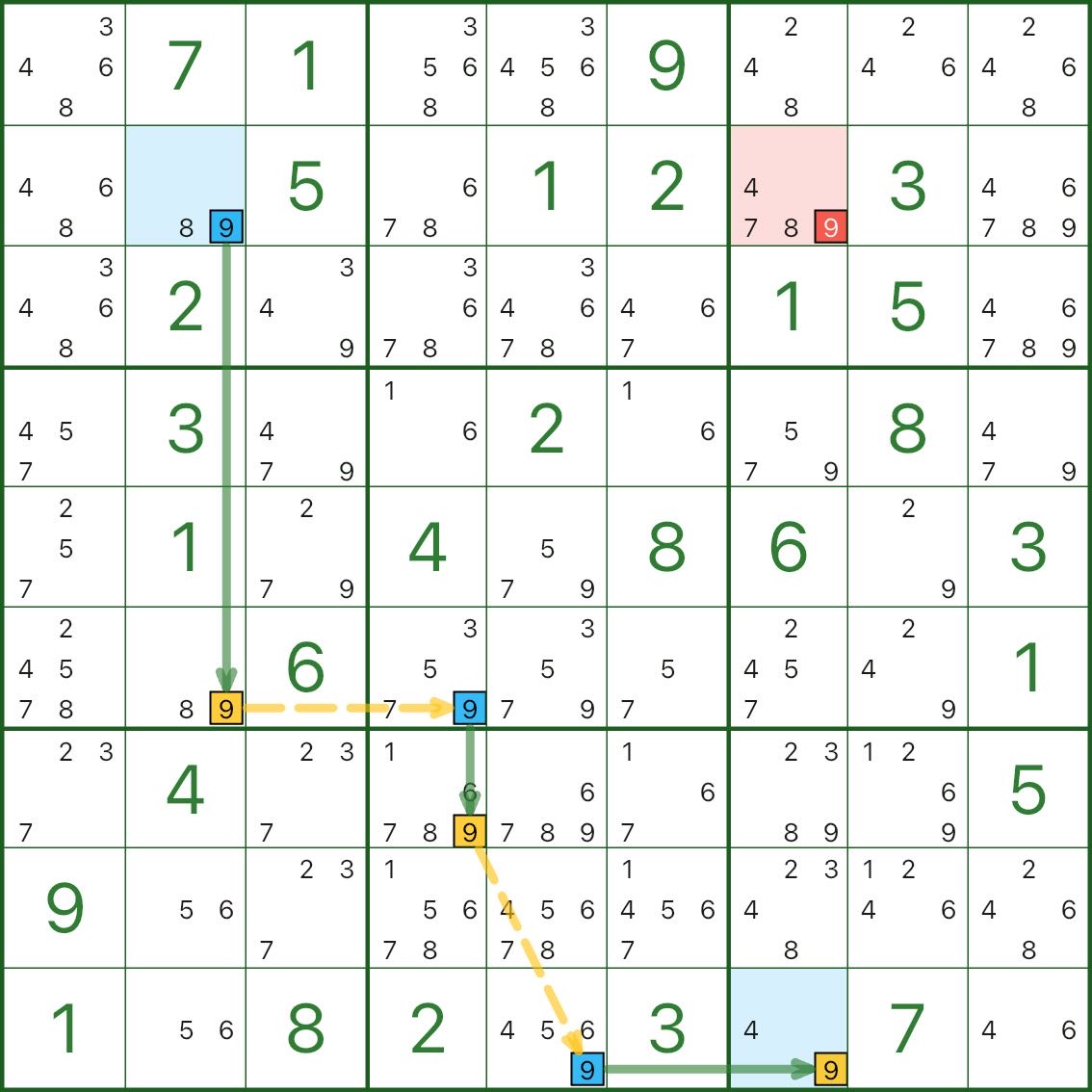
На диаграмме красный кандидат — это цифра 9 в r2c7.

Прочтите это так:

1. Из выделенного начала: как только r2c2 НЕ равен 9, цепочка распространяется до принудительного r9c7 = 9
   (видно четкое чередование Ложь → Верно → Ложь → Верно → Ложь → Верно)

2. Теперь воспользуемся противоречием: предположим, что красный кандидат r2c7 = 9 истинен.

   • r2c7 видит r2c2 в той же строке, поэтому r2c2 не может быть 9 (r2c2(9) — ложь)
   • распространить это «ложь» по цепочке, заставляя r9c7(9) быть истинным
   • r2c7 и r9c7 находятся в одном столбце, поэтому они не могут оба быть 9 → противоречие

Следовательно, r2c7 не может быть 9, и этого красного кандидата можно исключить.

---

Практика

Следующие три диаграммы представляют собой однозначные цепочки. Не торопись.

Три быстрых вопроса для самопроверки:

1. Какие сегменты являются сильными связями и почему они «или-или»?
2. Какие сегменты являются слабыми звеньями и почему они взаимоисключающие?
3. Почему красный кандидат приводит к противоречию?

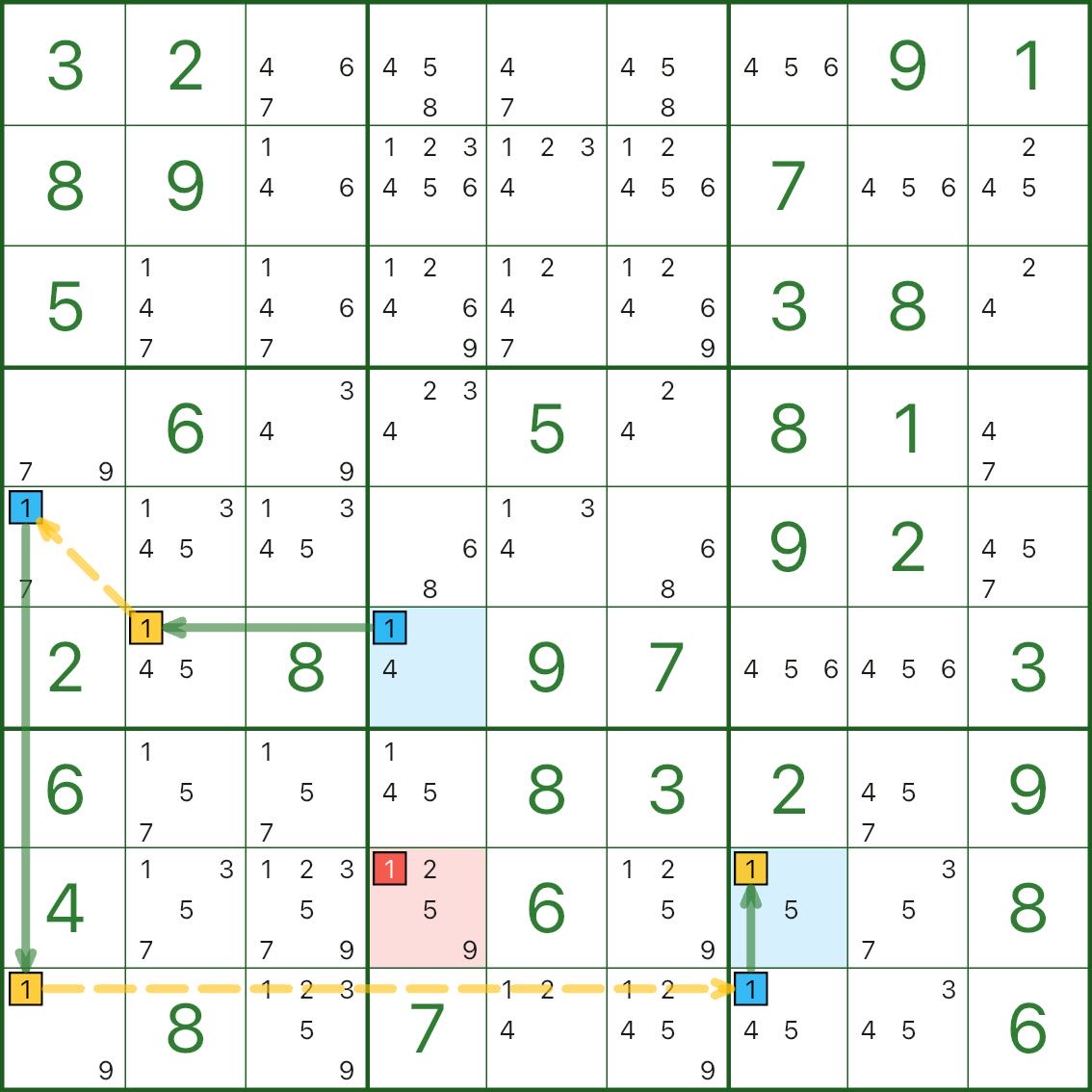
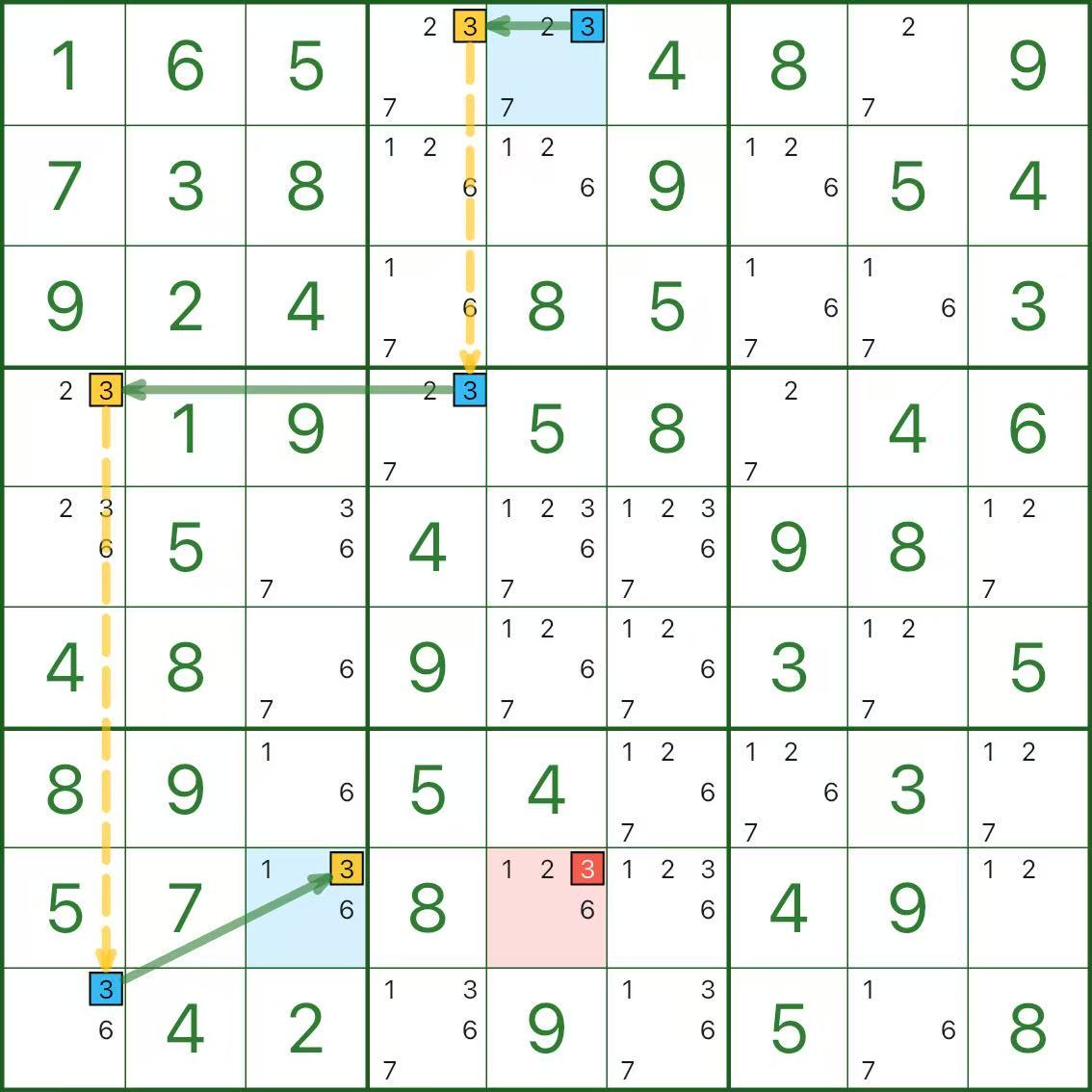
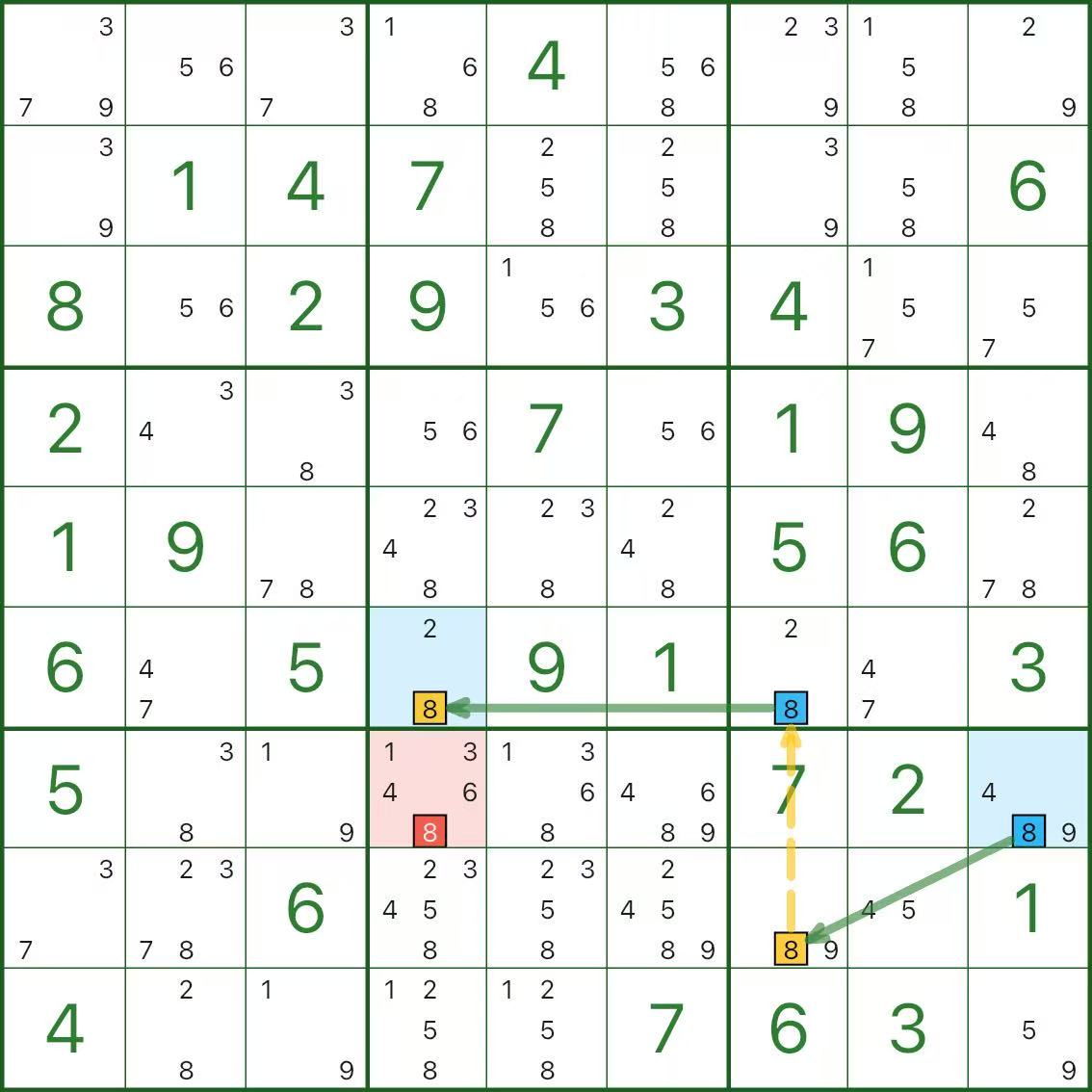
Если поначалу кажется, что это немного извилисто, это совершенно нормально.
Это цепочка: основа многих продвинутых техник — освойтесь с ней, прежде чем двигаться дальше.