Asa XYZ

Descrição

XYZ-Wing é semelhante a XY-Wing: ambos usam um padrão “pivô + duas asas” para eliminar um candidato compartilhado por contradição.
A principal diferença é que o pivô tem três candidatos na asa XYZ, então a célula de eliminação normalmente precisa ver o pivô e ambas as alas (porque o candidato compartilhado também pode ser colocado no pivô).

A estrutura é semelhante a esta (foco no candidato compartilhado z):

• Pivot (azul): candidatos x, y, z
• Asas (amarelas): {x, z} e {y, z}

Conclusão: em qualquer célula que consiga ver o pivô e ambas as asas, o candidato z pode ser eliminado.

---

Explicação

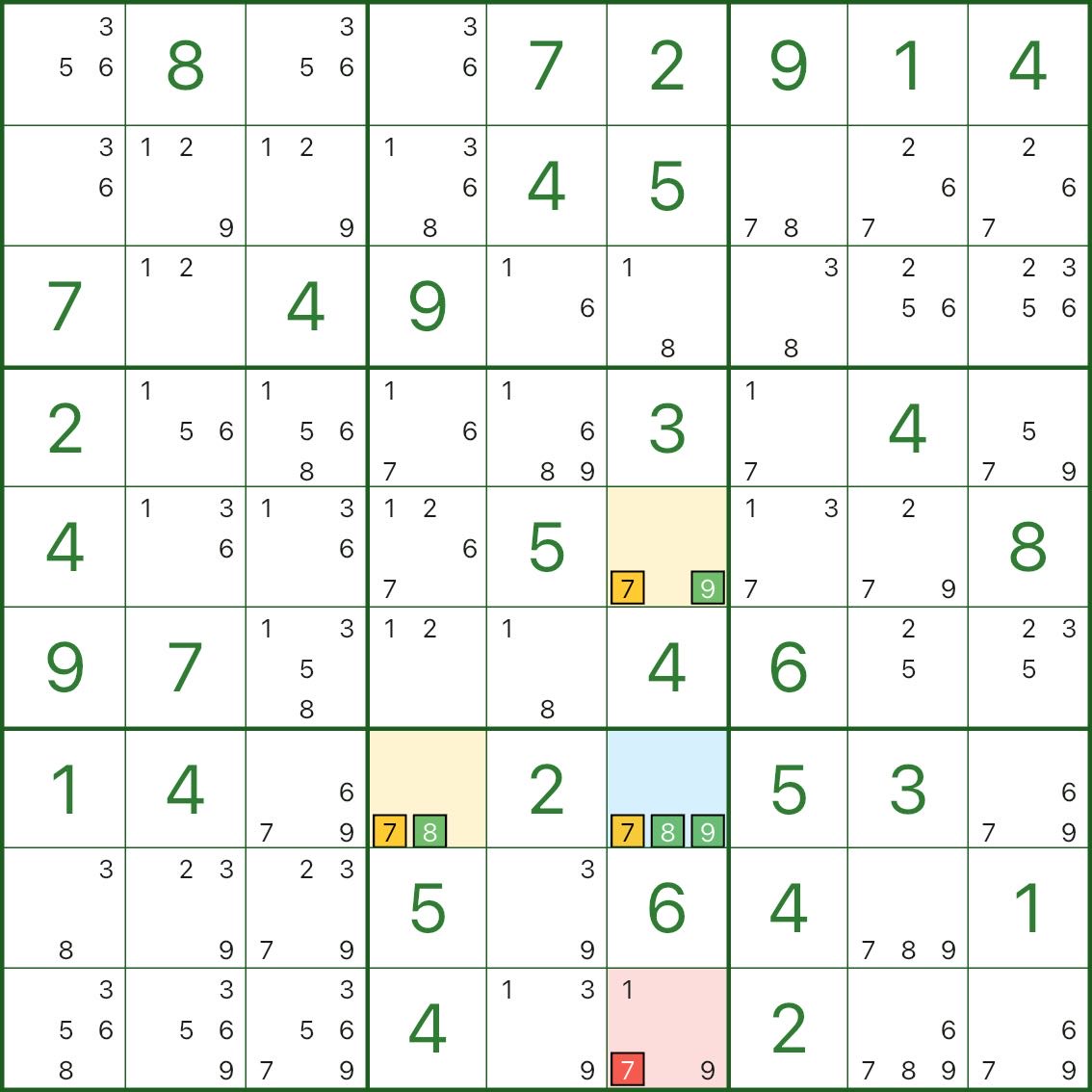
Na imagem acima, queremos eliminar o candidato 7 em r9c6 (vermelho).
O pivô azul é r7c6, com candidatos 7, 8, 9.
As duas asas amarelas são:

• r5c6: candidatos 7 e 9
• r7c4: candidatos 7 e 8

Por que podemos remover 7 de r9c6? Basta uma pequena contradição:

• Suponha r9c6 = 7 (o candidato vermelho é verdadeiro)
• r9c6 pode ver ambas as asas, então 7 é removido de ambas as asas:
  • r5c6 deve ser 9
  • r7c4 deve ser 8
• Agora o pivô r7c6 não tem mais valor:
  • r9c6 = 7 ⇒ r7c6 não pode ser 7 (mesma coluna)
  • r5c6 = 9 ⇒ r7c6 não pode ser 9 (mesma coluna)
  • r7c4 = 8 ⇒ r7c6 não pode ser 8 (mesma linha)
  • r7c6 só tinha {7,8,9} ⇒ nenhum valor se ajusta (contradição)

Portanto, a suposição é impossível: r9c6 não pode ser 7 e o candidato 7 pode ser eliminado.

---

Exemplos

Essas imagens mostram mais padrões de asas XYZ. Tente identificar a mesma estrutura: pivô (azul) / duas asas (amarelo) / eliminação (vermelho).

---

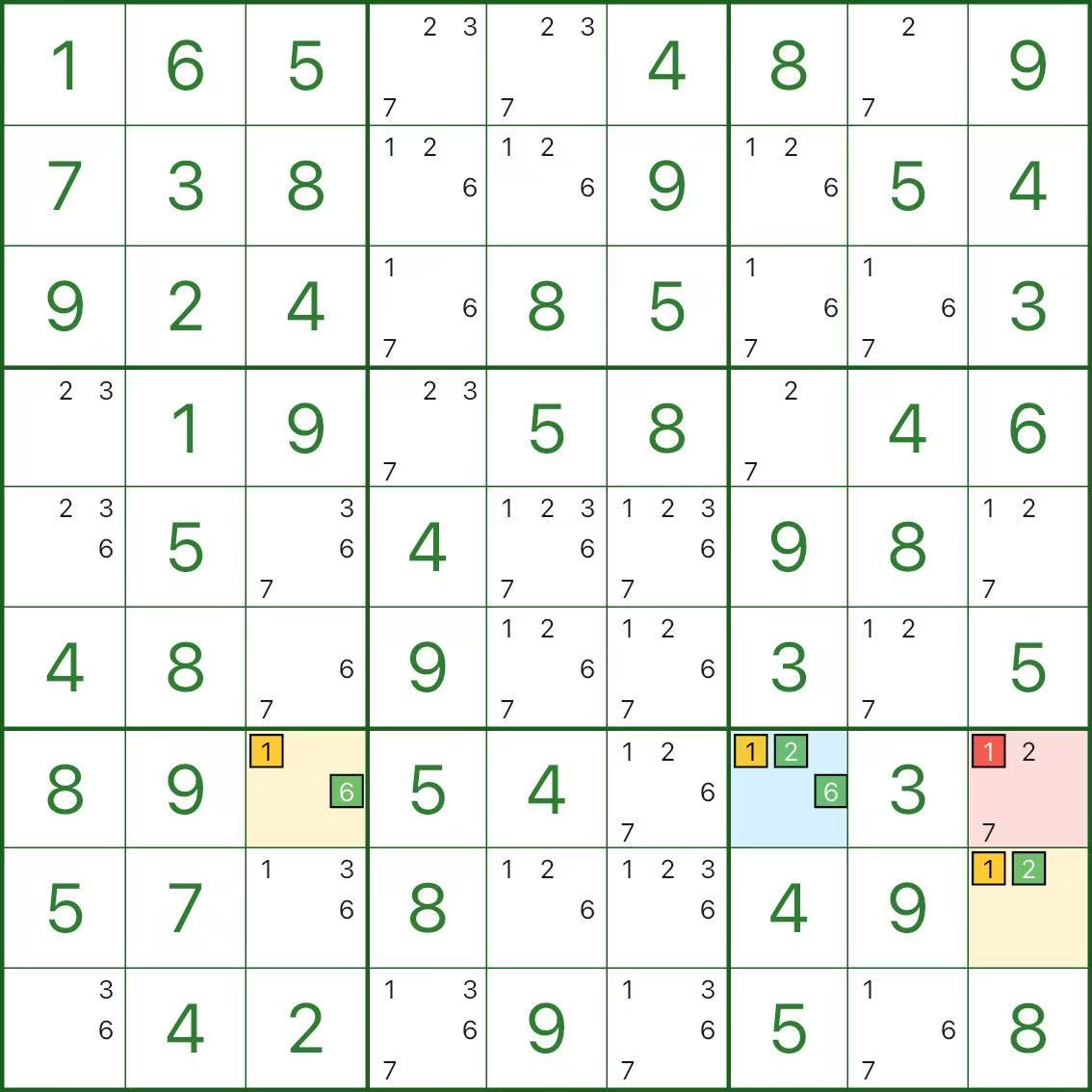
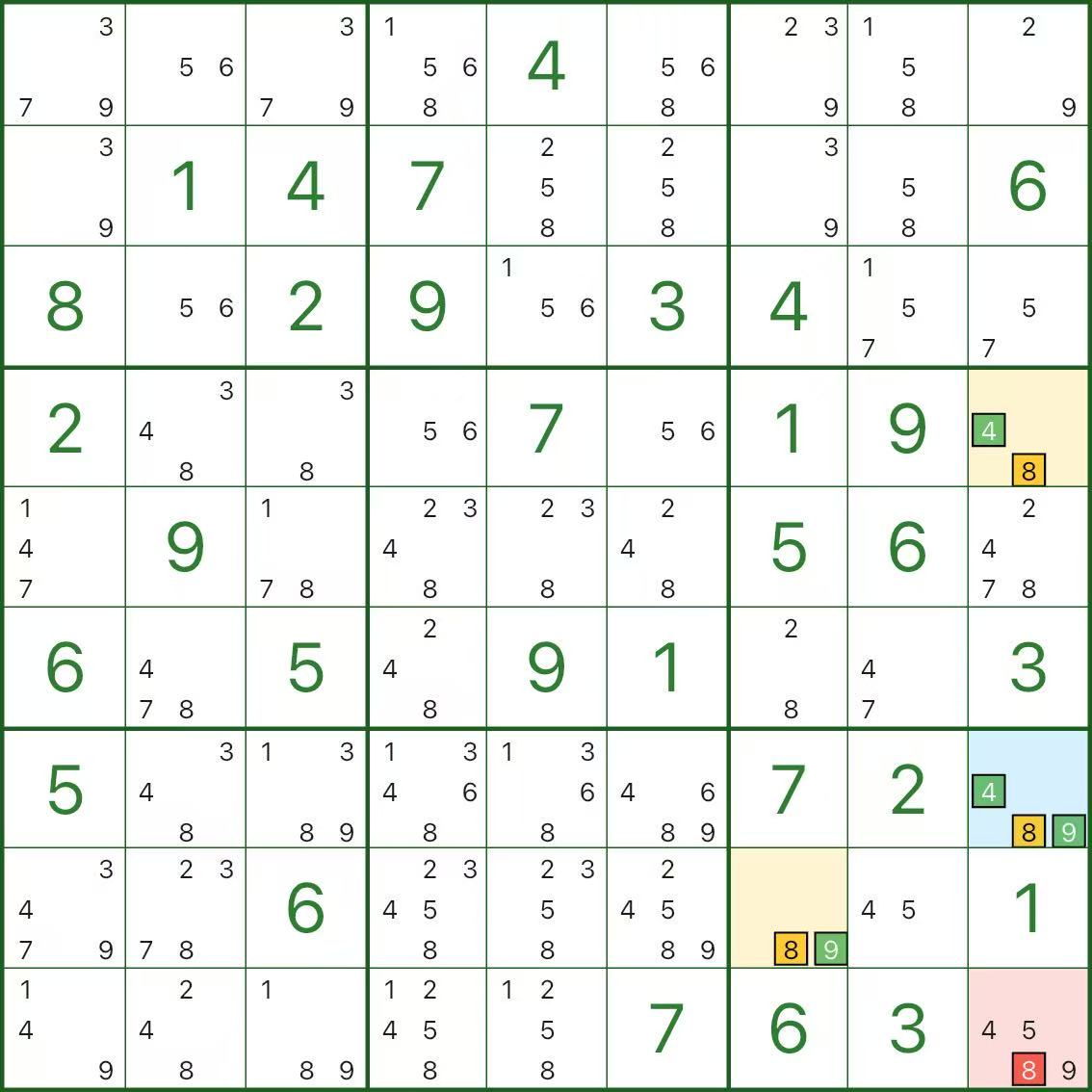
Como encontrar a asa XYZ

Lista de verificação de uma linha: encontre um pivô de 3 candidatos {x,y,z}, encontre duas asas de dois valores {x,z} e {y,z} e, em seguida, elimine z de qualquer célula que veja o pivô e ambas as asas.

Em um verdadeiro quebra-cabeça:

1. Encontre uma célula com exatamente três candidatos como pivô (azul)
2. Encontre duas células que possam ver o pivô, cada uma com exatamente dois candidatos, em formato de {x,z} e {y,z} (amarelo)
3. Encontre uma célula que possa ver o pivô e ambas as asas: remova o candidato z lá (vermelho)