Retângulo Único (UR)

Pré-requisito: UR depende do fato de que o quebra-cabeça tem exatamente uma solução.
Se você ainda não leu, comece aqui:
Uniqueness

---

1. Visão geral

Unique Rectangle (UR) é uma família de técnicas que usa a propriedade solução única para eliminar candidatos (e às vezes colocar um número).

Ele se concentra em uma “forma perigosa”:

• quatro células formam um retângulo 2×2 (duas linhas x duas colunas, abrangendo exatamente duas caixas)
• todos os quatro cantos contêm os mesmos dois candidatos principais (por exemplo, 1 e 7)

Se deixarmos essas quatro células apenas com esse par, o retângulo poderá muitas vezes ser preenchido de duas maneiras diferentes (trocando os dois dígitos), o que quebraria a exclusividade.
Portanto, sob a suposição de exclusividade, podemos concluir: alguns candidatos devem ser removidos ou uma célula deve assumir um valor específico.

---

2. Passo a passo (5 tipos)

As 5 imagens abaixo correspondem aos 5 tipos comuns de UR (as dicas do aplicativo os rotulam como Tipo I – V).

Guia de cores:

• Células azuis: o retângulo UR (a estrutura central)
• Marcas amarelas: candidatos nos quais estamos focando no raciocínio
• Marcas vermelhas: candidatos a eliminar/ou uma célula que pode ser definida

Tipo I: telhado único → um valor forçado

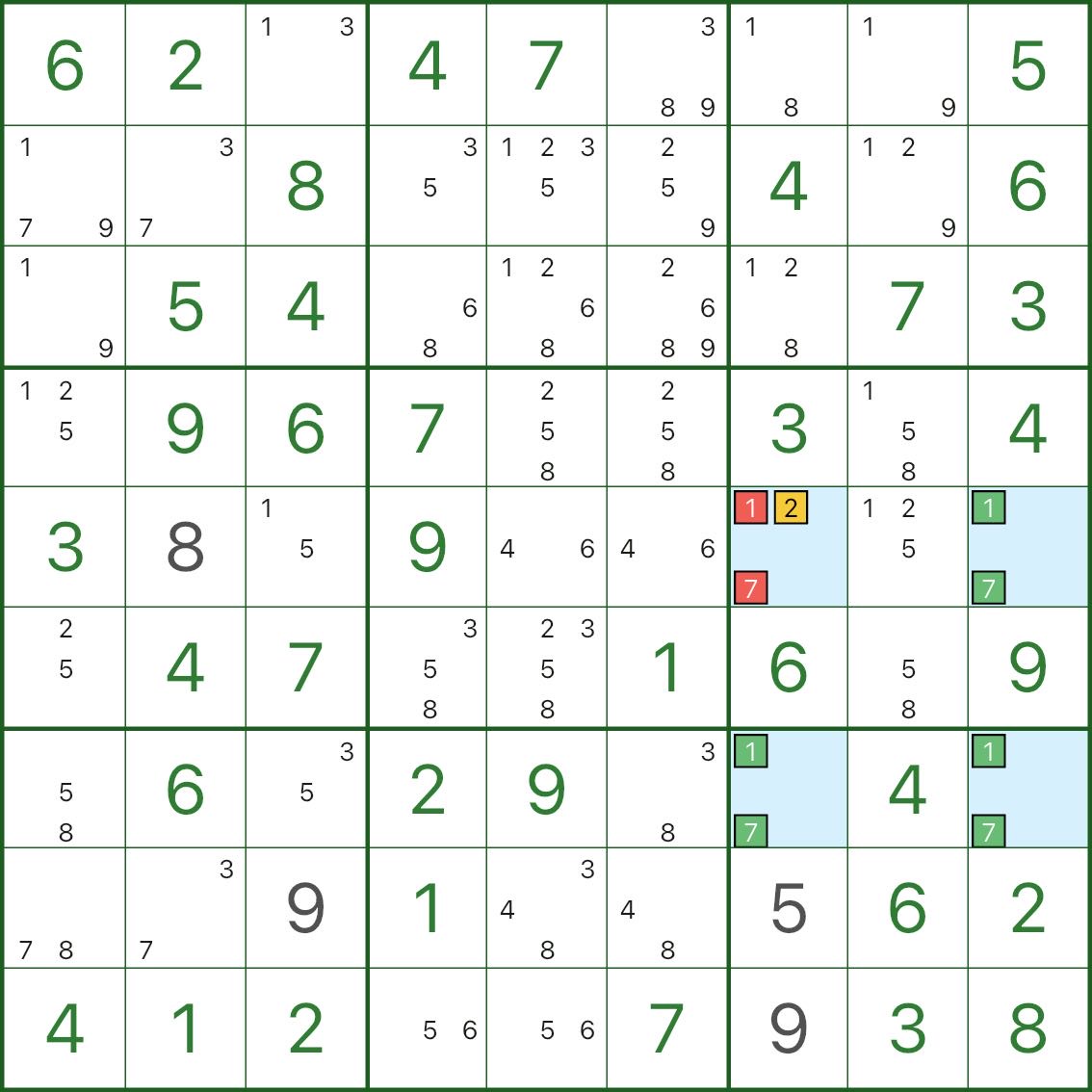
Observe as quatro células azuis: elas formam um retângulo e todas contêm os candidatos 1 e 7.
A célula r5c7 também possui um candidato extra 2.

Se 2 não for verdadeiro em r5c7, então r5c7 ficaria com apenas 1 e 7.
Isso tornaria todos os quatro cantos “apenas {1,7}”, permitindo dois preenchimentos trocáveis (quebrando a exclusividade).

Então, sob exclusividade:

• r5c7 não pode manter os candidatos 1 e 7
• portanto r5c7 deve ser 2

---

Tipo II: dois telhados → eliminar c que vê ambos os telhados

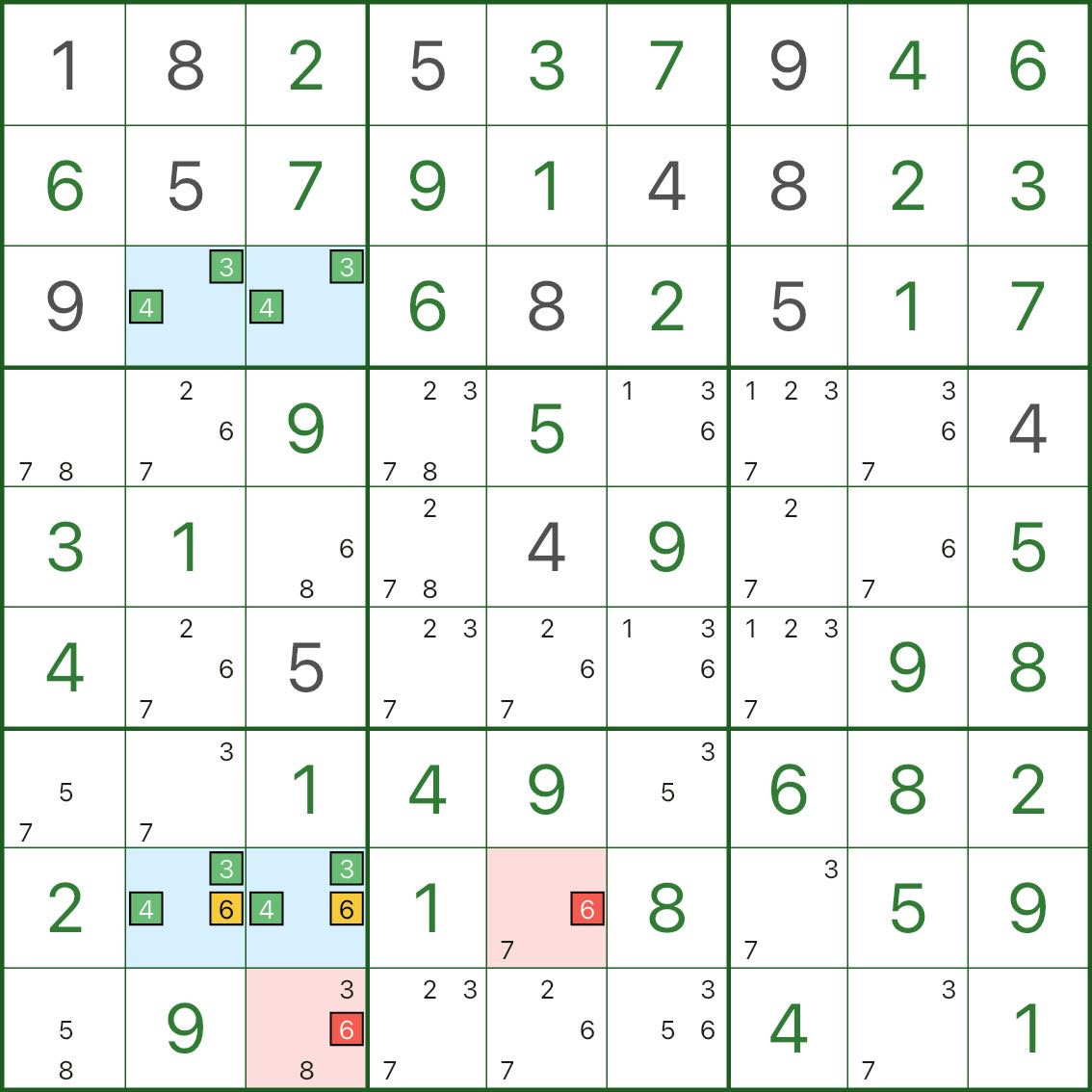
Aqui, o retângulo azul é baseado nos candidatos principais 3 e 4.
Duas células azuis r8c2 e r8c3 também contêm o candidato 6 (portanto, são {3,4,6}).

Agora considere um candidato vermelho 6 (por exemplo em r8c5 ou r9c3) que pode ver ambas células do telhado:

• se aquele vermelho 6 fosse verdade, ambos os telhados seriam forçados não 6
• os telhados desmoronariam apenas para {3,4}
• o retângulo se torna um padrão mortal {3,4} novamente (quebrando a exclusividade)

Portanto, esses 6 candidatos vermelhos não podem ser verdadeiros e podem ser eliminados.

---

Tipo III: tratar os telhados como um “pacote” e formar um subconjunto

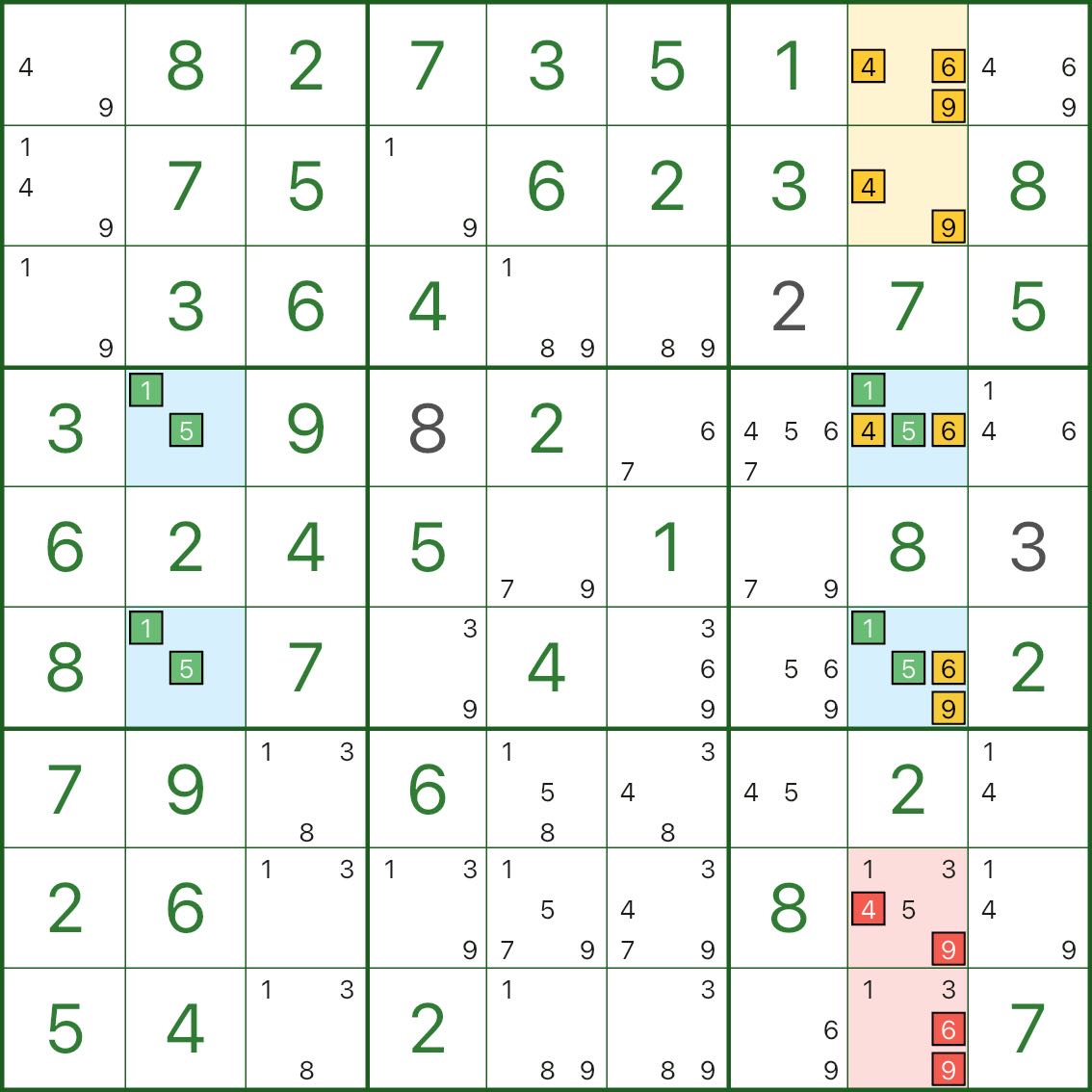
Este se concentra na coluna 8:

• duas células azuis na coluna 8 contêm candidatos principais 1 e 5
• eles também compartilham dígitos extras 4, 6, 9 (então cada um é {1,5,4,6,9})

A exclusividade impõe uma restrição importante:

• entre essas duas células azuis, pelo menos uma deve ter um dígito de {4,6,9}
• caso contrário, ambos dependeriam apenas de {1,5}, transformando o retângulo em um padrão mortal

Portanto, podemos tratar “os dígitos extras {4,6,9} das duas células azuis” como um pacote.
Juntamente com as células amarelas r1c8 e r2c8, isso bloqueia efetivamente os dígitos 4, 6, 9 dentro de um pequeno subconjunto na coluna 8.

Portanto, quaisquer outros candidatos 4/6/9 na coluna 8 (marcados em vermelho) podem ser eliminados.

---

Tipo IV: um par conjugado força um dígito → elimina o outro

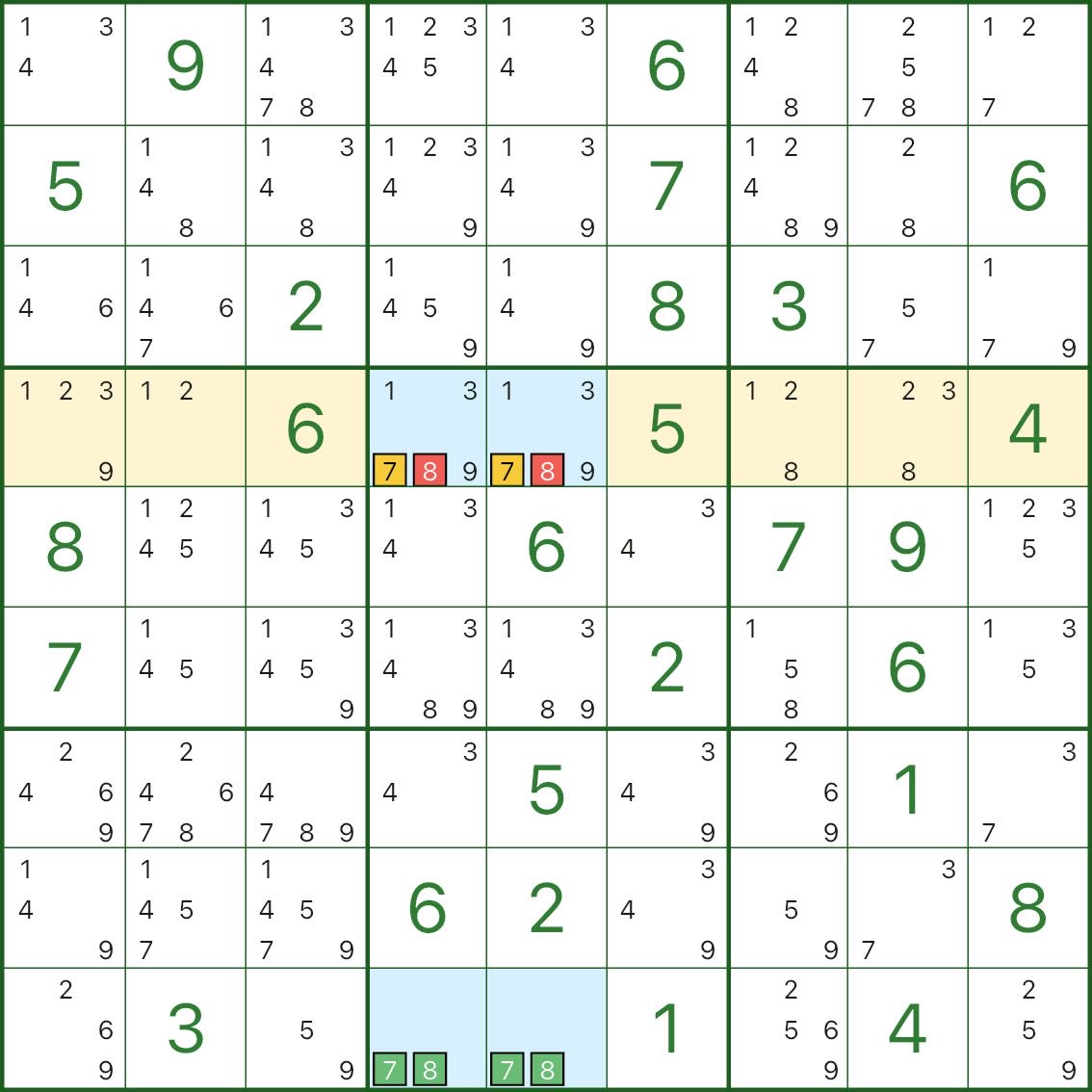
O retângulo azul é construído novamente em um par de núcleos (aqui 7 e 8).Na linha 4, o candidato 7 aparece apenas nas duas células azuis r4c4 e r4c5.
Isso significa:

• um de r4c4/r4c5 deve ser 7

Com essa restrição, manter o candidato 8 nessas mesmas células azuis ainda permitiria que o retângulo colapsasse em uma estrutura mortal (quebrando a exclusividade).

Portanto, podemos eliminar 8 de r4c4 e r4c5.

---

Tipo V: telhados múltiplos (2 ou 3) → eliminar c que vê todas as células do telhado

O Tipo V não é estritamente “três telhados”. A ideia principal é:

• existem 2 ou 3 células do telhado no retângulo e todas compartilham o mesmo candidato extra c
• se houver apenas 2 células no telhado, elas normalmente não compartilham a mesma linha/coluna/caixa (se compartilharem, é mais próximo do Tipo II)
• se o candidato de uma célula c puder ver todas essas células do telhado, então esse c não pode ser verdadeiro e pode ser eliminado

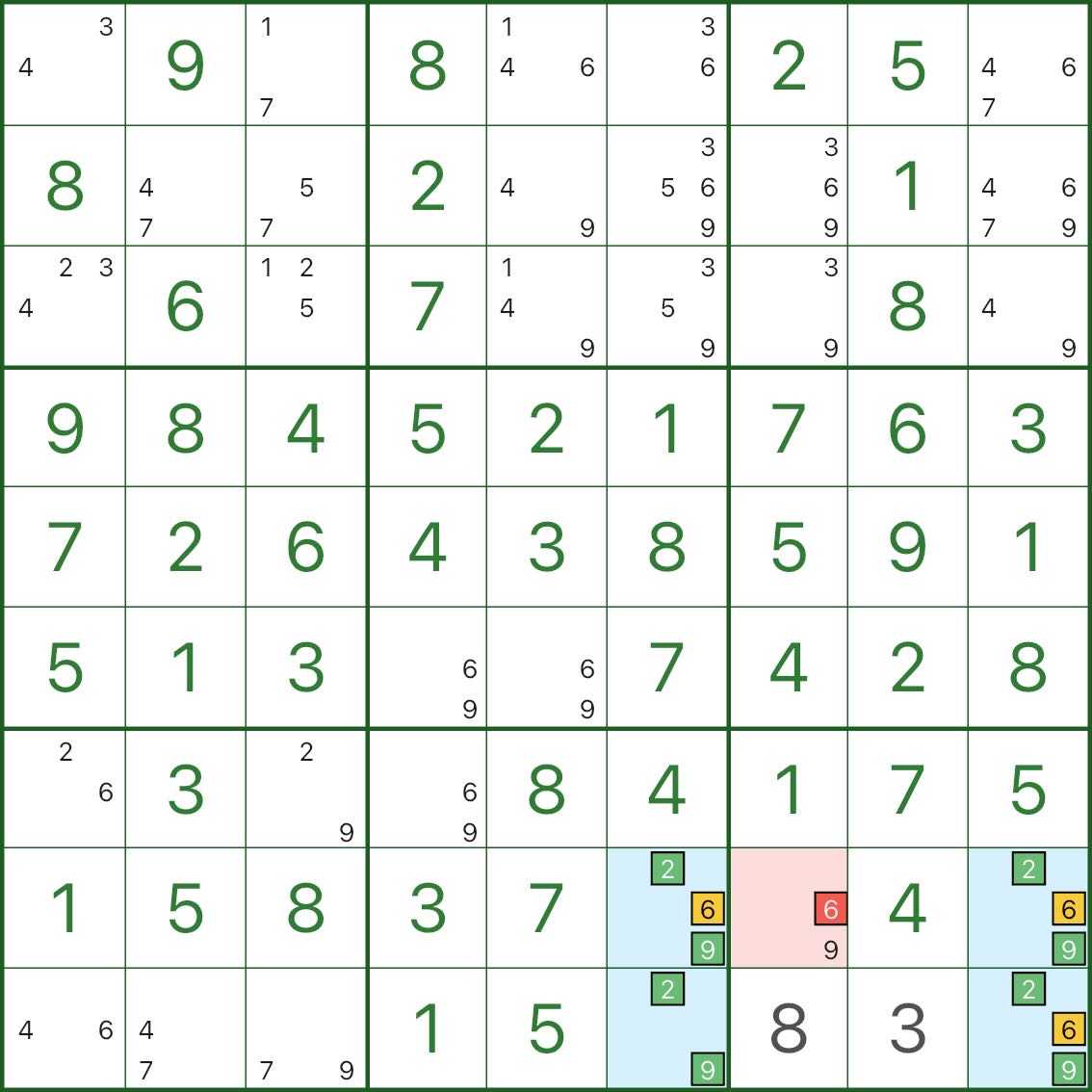
Nesta imagem, o retângulo azul envolve principalmente os dígitos 2, 6, 9:

• três cantos azuis são {2,6,9}
• o canto azul restante é {2,9} (faltando 6)

Agora olhe para a célula vermelha r8c7: ela tem o candidato 6 e pode ver todas as {2,6,9} células do telhado neste padrão.

Se r8c7 = 6:

• todas as três células do telhado seriam forçadas a não-6
• eles entrariam em colapso apenas em {2,9}
• o retângulo se torna um padrão {2,9} mortal (quebrando a exclusividade)

Portanto, o candidato 6 em r8c7 não pode ser verdadeiro e pode ser eliminado.

---

3. Exemplos

As imagens 1–5 neste artigo já são exemplos do Tipo I–V.
Ao praticar, tente localizar primeiro o retângulo azul e, em seguida, combine as marcas amarelas/vermelhas com o raciocínio acima.

---

4. Como identificar um retângulo único

Em quebra-cabeças reais, você pode pesquisar nesta ordem:

1. Procure quatro células vazias que formam um retângulo 2×2 (duas linhas x duas colunas) e ocupam exatamente duas caixas
2. Verifique se todos os quatro cantos compartilham os mesmos dois candidatos principais (o “par mortal”)
3. Em seguida, classifique pela aparência dos candidatos extras:
   • apenas um canto possui candidatos extras → Tipo I (geralmente um valor forçado)
   • dois cantos compartilham o mesmo dígito extra c → Tipo II
   • os dígitos extras dos telhados podem formar um subconjunto em uma linha/coluna/caixa → Tipo III
   • em uma casa, um dígito central aparece apenas em duas células retangulares → Tipo IV
   • dois ou três cantos compartilham o mesmo dígito extra c (para 2 telhados, geralmente não compartilham uma casa) → Tipo V

Isso é UR em uma frase: nunca permita que o retângulo entre em colapso em um padrão mortal – caso contrário, a exclusividade seria quebrada.