Pares e subconjuntos

Pares e subconjuntos nus/ocultos

Pares e subconjuntos são algumas das técnicas mais úteis de “eliminação de candidatos”. Eles têm nomes diferentes, mas todos fazem a mesma coisa:

Em uma casa (uma linha/coluna/caixa), um pequeno conjunto de células e um pequeno conjunto de dígitos “reservam os espaços” um para o outro — para que esses dígitos não possam aparecer em outro lugar daquela casa.

Você não precisa memorizar o jargão. Uma regra simples:

• Naked: comece pelo que as células mostram (essas células contêm apenas esses dígitos)
• Oculto: comece de onde um dígito pode ir (esses dígitos só podem ir nessas células)

---

1. Par Nu

Na mesma casa, se duas células contiverem apenas os mesmos dois candidatos (por exemplo {a,b}), você terá um par nu.

Isso significa:

• Uma célula deve ser a, a outra deve ser b (ordem desconhecida)
• Assim, os candidatos aeb podem ser removidos de todas as outras células vazias daquela casa

Primeiro, observe a imagem abaixo: concentre-se na Caixa 3 destacada e nas duas células verdes r2c9 e r3c9.
Você notará que eles só podem ser {1,5}.

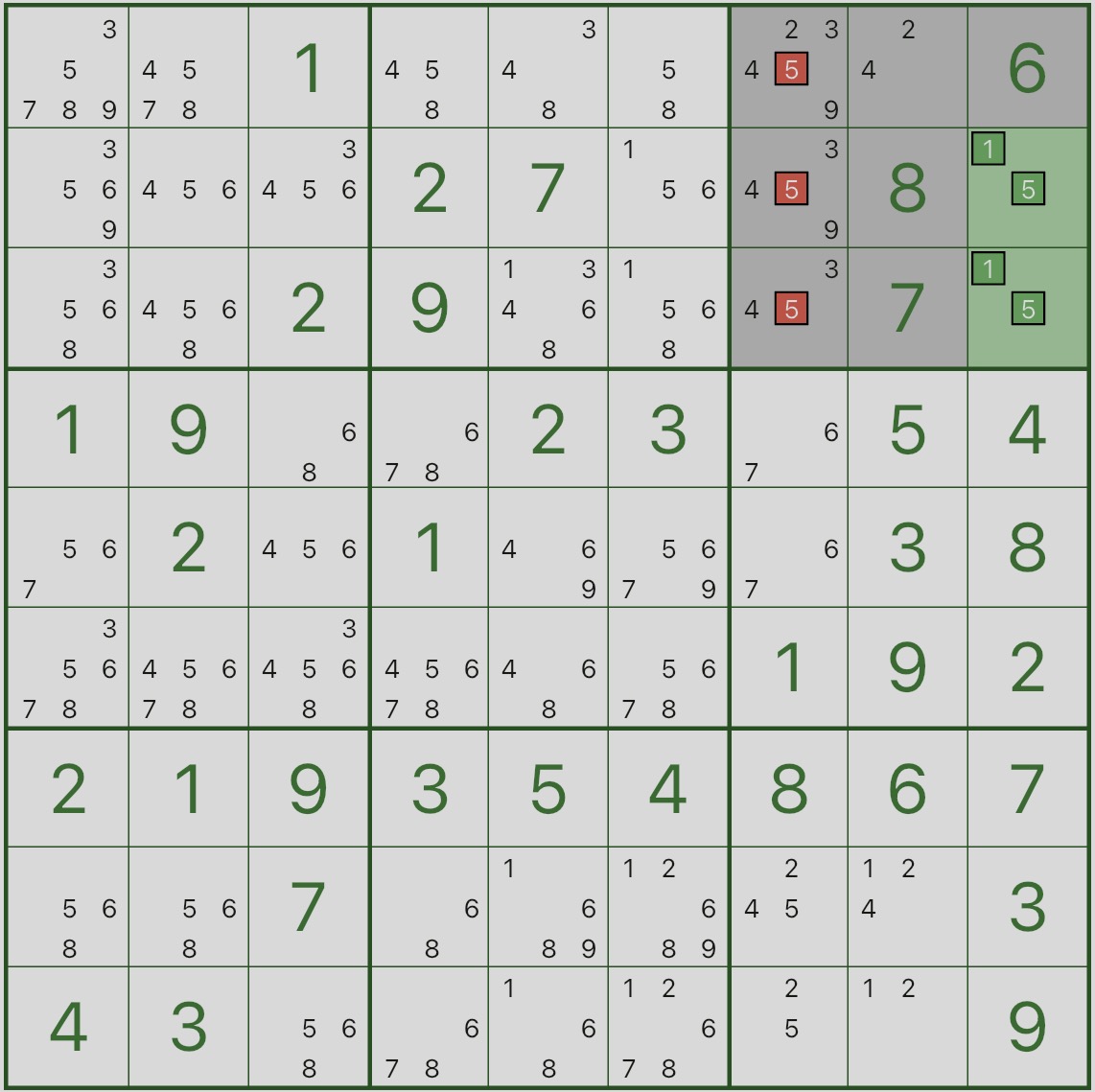
Isso significa: na Caixa 3, os dígitos 1 e 5 estão “reservados” para r2c9 e r3c9.

Agora observe os candidatos vermelhos: o candidato 5 em r1c7, r2c7, r3c7 pode ser removido.

Uma prova rápida por contradição:

• Suponha que r1c7 seja 5 (a mesma lógica se aplica a r2c7 e r3c7)
• Então a Caixa 3 já contém um 5, então r2c9 e r3c9 não podem ser 5 e são forçados a ser 1
• Mas r2c9 e r3c9 compartilham a mesma coluna (coluna 9), então ambos não podem ser 1 — contradição
  ⇒ aqueles 5 candidatos vermelhos são impossíveis e podem ser removidos

---

2. Par oculto

Na mesma casa, se o candidato a aparecer em exatamente duas células, e o candidato b também aparecer nas mesmas duas células, você terá um par oculto.

Essas duas células podem mostrar candidatos extras, mas a e b já estão bloqueados para elas, então você pode:

• Remova todos os candidatos exceto a e b dessas duas células

Primeiro, observe a imagem abaixo: foque na coluna 4 destacada.
Descubra onde os candidatos 4 e 5 aparecem nessa coluna — você verá que eles aparecem apenas em r1c4 e r6c4.

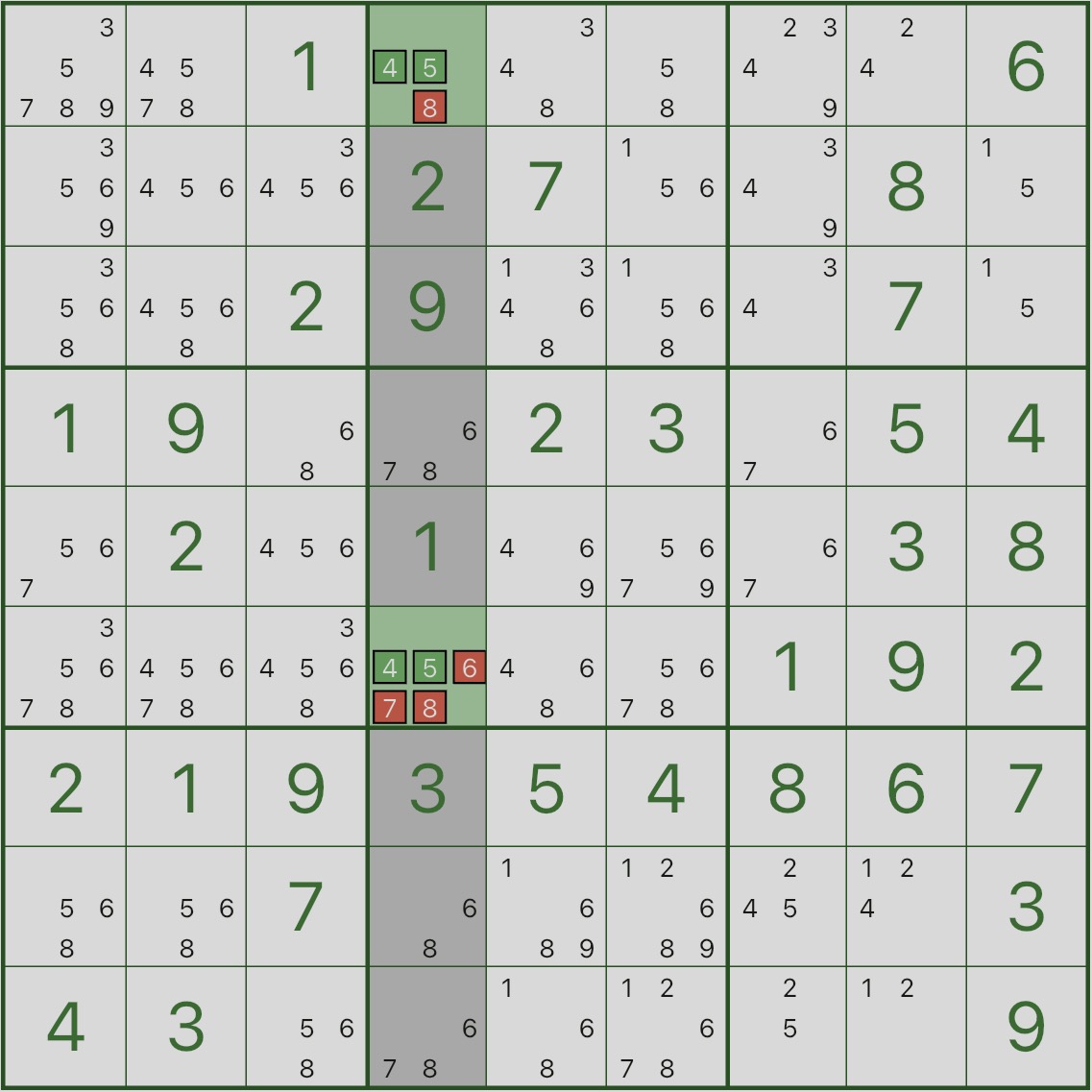
Isso significa: na coluna 4, os dígitos 4 e 5 devem ser colocados em r1c4 e r6c4.

Por que podemos remover outros candidatos de r1c4 e r6c4?

• Suponha que r1c4 pegue um dígito que não seja 4 ou 5
• Então tanto 4 quanto 5 teriam que caber em r6c4 apenas
• Uma única célula não pode ser 4 e 5 ao mesmo tempo – contradição
  ⇒ r1c4 e r6c4 devem ser {4,5}, para que outros candidatos nessas células possam ser removidos

---

3. Subconjunto nu (triplo / quádruplo)

Esta é a ideia do “par nu”, generalizada:

Se N células em uma casa contêm coletivamente apenas N dígitos (por exemplo, três células contêm apenas {a,b,c}), você tem um triplo nu. A mesma ideia se aplica aos quadríceps.

Esses dígitos devem ser colocados dentro dessas N células, então:

• Remova esses dígitos (por exemplo, a, b, c) de todas as outras células vazias daquela casa

Primeiro, observe a imagem abaixo: concentre-se na linha 8 destacada e nas três células r8c1, r8c2, r8c4.
Você notará que essas três células contêm coletivamente apenas {5,6,8}.

Isso significa: na linha 8, os dígitos 5, 6, 8 devem ser colocados dentro de r8c1, r8c2, r8c4.

É por isso que os candidatos 5, 6, 8 vermelhos no resto da linha 8 podem ser removidos.

Uma visão de contradição simples:

• Se outra célula na linha 8 “pegar” um de {5,6,8}
• Então essas três células teriam que ser preenchidas usando apenas dois dígitos para três células
• Isso não pode funcionar - contradição

---

4. Subconjunto oculto (triplo / quádruplo)

Esta é a ideia do “par oculto”, generalizada:

Se N dígitos em uma casa aparecerem apenas nas mesmas N células (mesmo que essas células contenham candidatos extras), você terá um triplo/quádruplo oculto.

Esses N dígitos estão bloqueados para essas N células, então:

• Remova todos os candidatos exceto os N dígitos dessas células

Primeiro, observe a imagem abaixo: foque na coluna 5 destacada.
Você notará que os dígitos 4,7,8 aparecem apenas em r1c5, r8c5, r9c5.

Isso significa: na coluna 5, os dígitos 4, 7, 8 devem ser colocados dentro de r1c5, r8c5, r9c5.

Portanto, nessas três células podemos remover quaisquer outros candidatos que não sejam 4, 7 ou 8.

Por que isso é seguro?

• Se alguma dessas células tiver um dígito diferente
• Então 4, 7 e 8 teriam menos de três espaços para caber – contradição

---

5. Dicas para identificá-los mais rapidamente

• Mantenha os candidatos razoavelmente completos (você precisará deles para quebra-cabeças mais difíceis)
• Procure primeiro padrões nus: comece a partir de células com poucos candidatos (2, 3 ou 4)
• Em seguida, procure padrões ocultos: em uma casa, verifique se um dígito está limitado a 2, 3 ou 4 pontos
• Após as eliminações, faça uma pausa e olhe novamente – os candidatos simplificados geralmente revelam o próximo passo