Guias / Noções básicas de cadeias
Noções básicas de cadeias
> Elos fortes/elos fracos/alternância (AIC)
Advanced
Noções básicas de cadeias
Elos fortes/elos fracos/alternância (AIC)
As cadeias são um alicerce essencial para muitas técnicas avançadas de Sudoku.
No fundo, uma cadeia é apenas uma sequência de implicações “se…então…” que permite que as deduções percorram a grade.
Após este capítulo, dicas avançadas como cadeias de um dígito, pipa, arranha-céu, medusa e AIC parecerão muito mais legíveis.
Usamos r1c1 para nos referir a uma posição de célula:
r = linha, c = coluna.
Para tornar os diagramas mais fáceis de seguir, usamos:
- Linha sólida verde: elo forte
- Linha tracejada amarela: elo mais fraco
- Fundo candidato azul/amarelo: dois “estados” mutuamente exclusivos, para visualizar a alternância
- Candidato vermelho: o candidato a ser eliminado nesta etapa
Lembrete: uma cadeia é bidirecional. As setas são apenas para facilitar a leitura.
O que é uma cadeia?
Resumindo, uma cadeia conecta relações de candidatos para que você possa continuar aplicando a lógica “se…então…”:
Se A não for possível, então B deve ser verdadeiro;
se B for verdadeiro, então C deve ser falso;
…
Uma cadeia é feita de:
- Nós: candidatos (um candidato de dígito em uma célula)
- Elos: relações entre candidatos (fortes/fracos)
Uma cadeia não significa necessariamente “sempre apagamos o início”. É mais como um caminho de raciocínio:
- Alcance uma contradição ⇒ prove que um candidato não pode ser verdadeiro → elimine-o
- Alcance uma verdade forçada ⇒ provar que um candidato deve ser verdadeiro → coloque um valor
Este artigo se concentra nas “cadeias de um dígito” mais comuns: raciocínio sobre candidatos de um dígito d.
(As relações entre células bivalores e ligações fortes agrupadas/regiões serão abordadas posteriormente.)
Elos fortes e elos fracos
Elo forte (par conjugado)
Mnemônico: ou-ou.
Na mesma unidade (linha/coluna/caixa), se um dígito d aparecer em exatamente duas células candidatas, esses dois candidatos formam um vínculo forte (um par conjugado).
A principal implicação é “NÃO força SIM”:
- Se NÃO A, então B (Se A não é d, então B deve ser d)
- Se NÃO B, então A
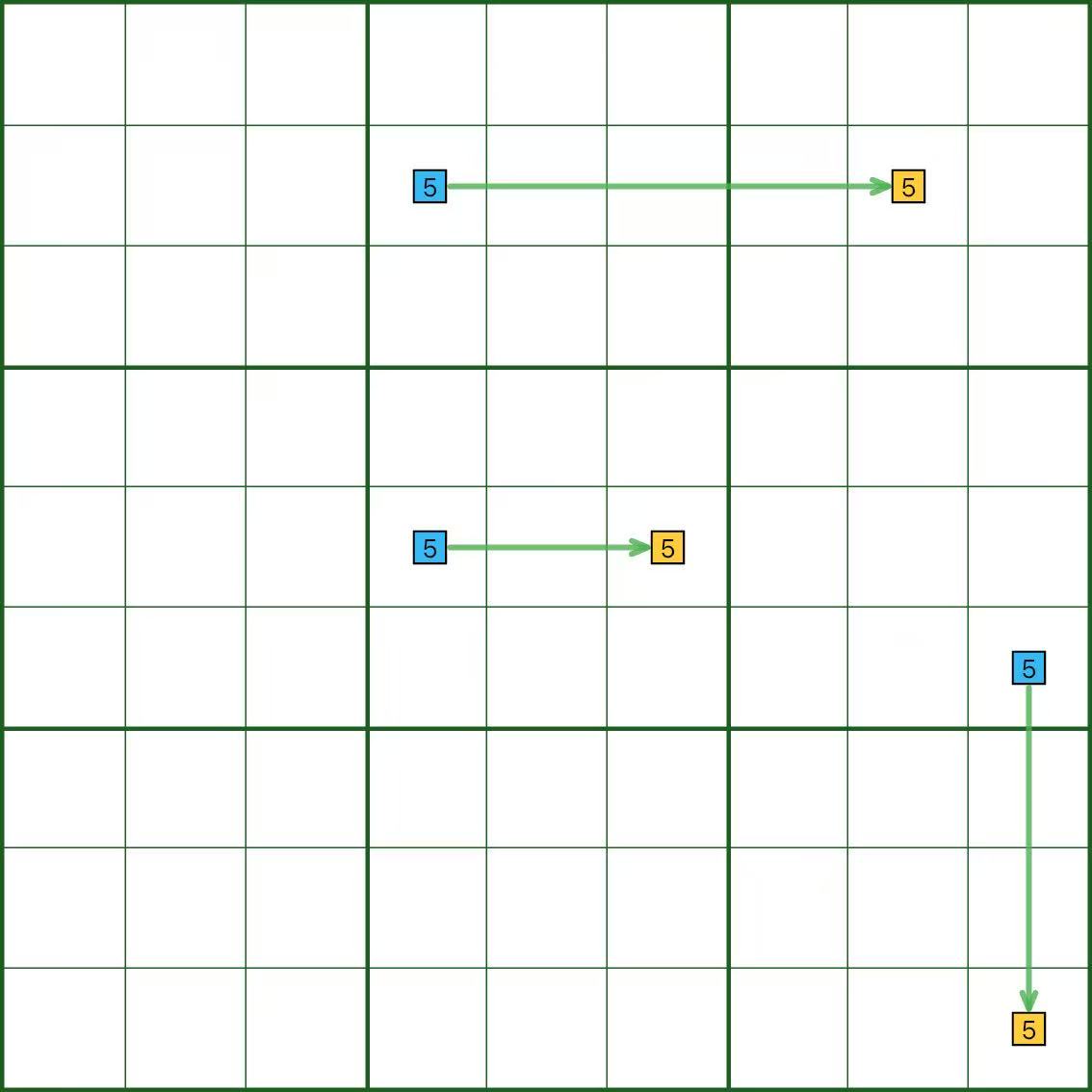
No diagrama, o dígito 5 forma ligações fortes em uma linha, uma coluna e uma caixa.
Você pode lê-lo de qualquer lado; as setas são apenas um auxílio à leitura.
Nota importante: todo elo forte é também um elo fraco.
Como os dois candidatos compartilham a mesma unidade, ambos não podem ser verdadeiros:
- Se A, então NÃO B (Se A é d, então B não é d)
Resumo de uma linha:
Elo forte = exclusividade fraca + “um deles deve ser verdadeiro”
Elo fraco
Mnemônico: se vocês se veem, ambos não podem ser verdadeiros.
Um elo fraco expressa uma coisa:
Dois candidatos não podem ser ambos verdadeiros.
Em cadeias de um dígito, o elo fraco mais comum são dois candidatos do mesmo dígito d na mesma unidade.
Implicação:
- Se A, então NÃO B
Mas não o inverso:
- Se A for falso, você não pode concluir B (pode haver um terceiro ponto).
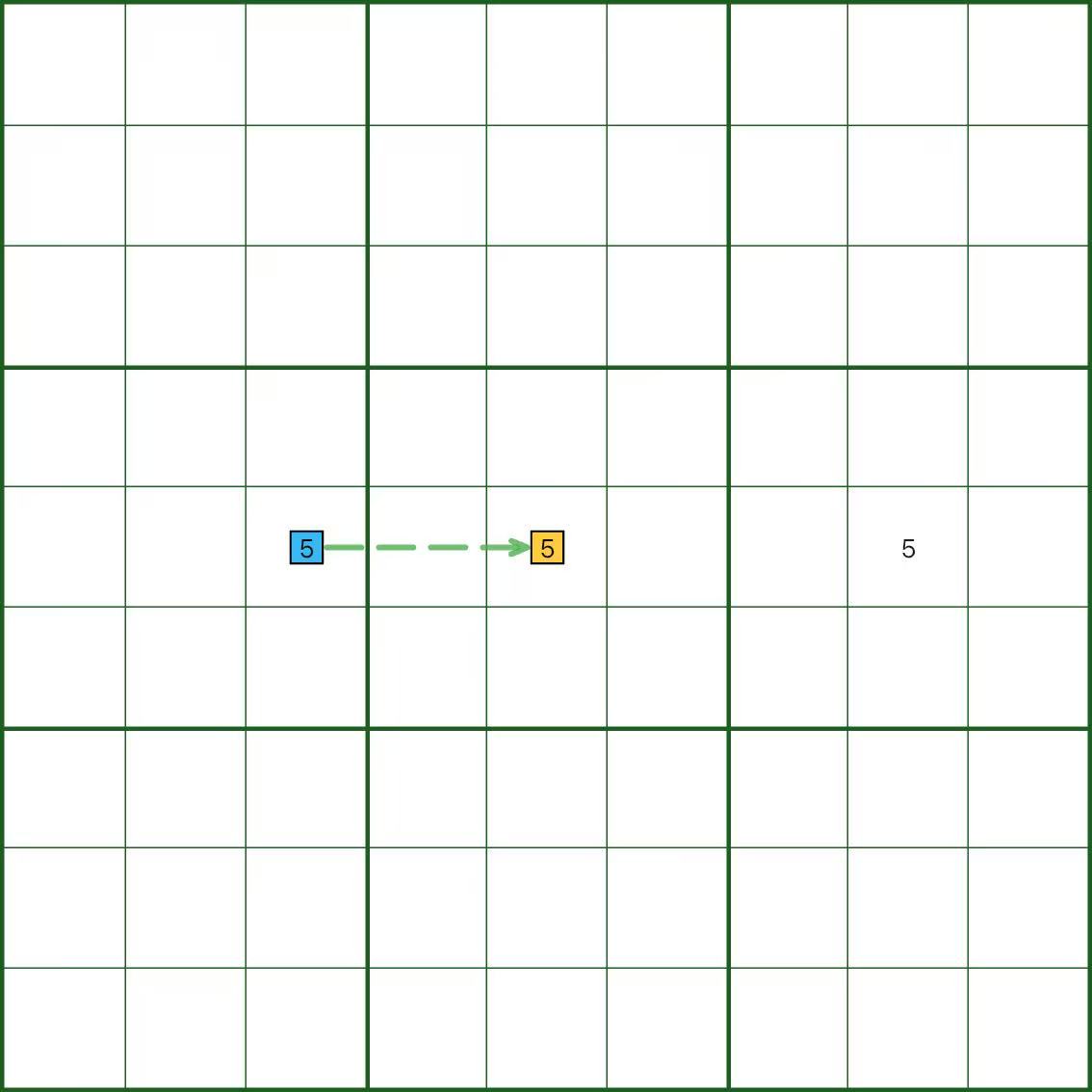
No diagrama, o dígito 5 tem três células candidatas seguidas, portanto cada par está fracamente vinculado.
A imagem desenha apenas um segmento tracejado apenas para mostrar a aparência de um elo fraco.
Como funcionam as cadeias?
Para propagar ao longo de uma cadeia, lembre-se de duas regras:
- Verdadeiro → (fraco) → Falso
Os elos fracos são exclusivos: se A for verdadeiro, B deve ser falso. - Falso → (forte) → Verdadeiro
Elos fortes são ou-ou: se A for falso, o outro candidato deve ser verdadeiro.
Portanto, uma cadeia de trabalho normalmente alterna:
Falso —(forte)→ Verdadeiro —(fraco)→ Falso —(forte)→ Verdadeiro —(fraco)→ Falso…
Por que alternar?
- quebras fracas-fracas: “falso” não se propaga através de um elo fraco
- forte-forte pode conectar, mas em muitos quebra-cabeças geralmente corresponde a padrões mais simples, então cadeias são mais úteis para propagação alternada
Exemplo
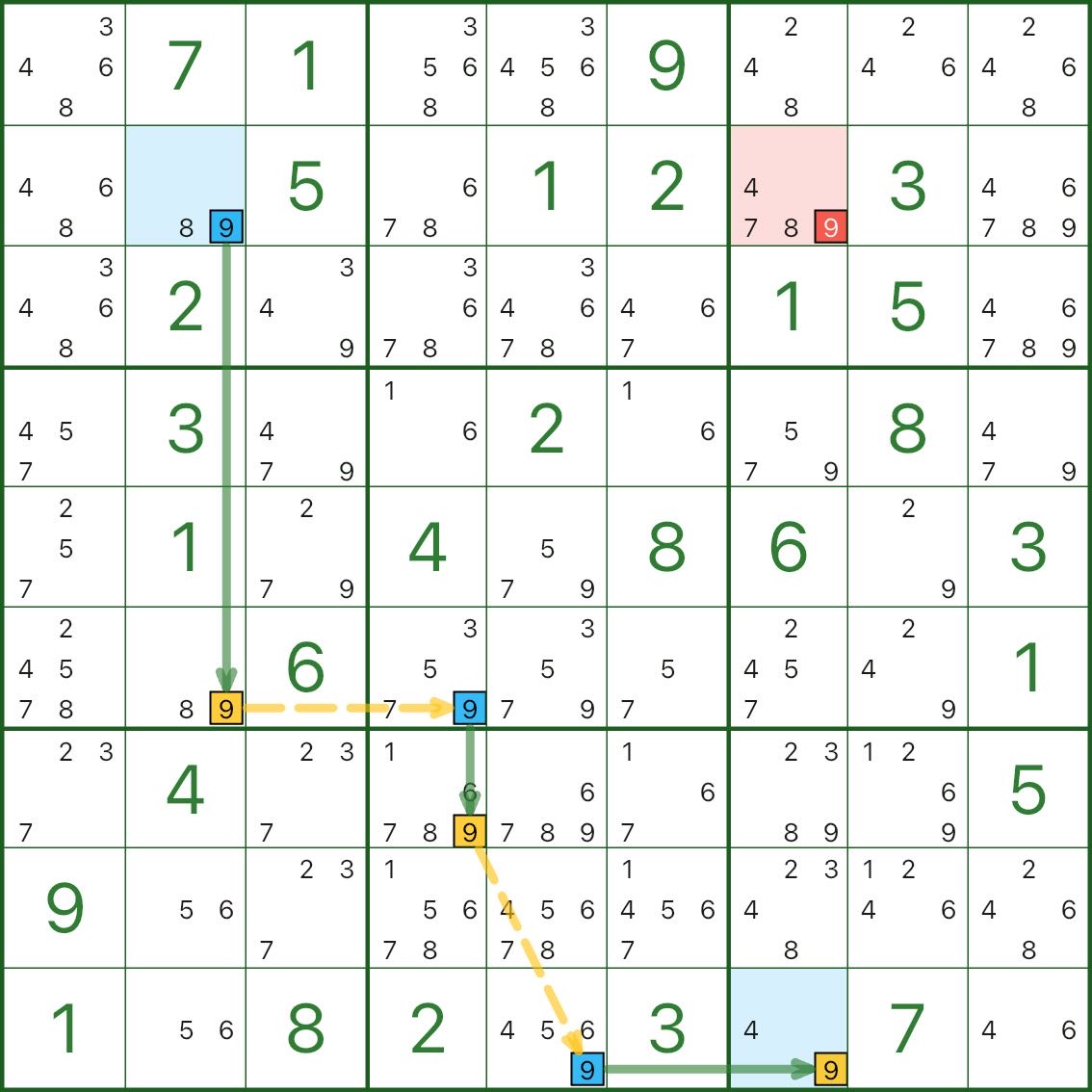
No diagrama, o candidato vermelho é o dígito 9 em r2c7.
Leia assim:
Do início destacado: uma vez que r2c2 NÃO é 9, a cadeia se propaga para forçar r9c7 = 9
(você pode ver a alternância limpa Falso → Verdadeiro → Falso → Verdadeiro → Falso → Verdadeiro)Agora use uma contradição: suponha que o candidato vermelho r2c7 = 9 seja verdadeiro
- r2c7 vê r2c2 na mesma linha, então r2c2 não pode ser 9 (r2c2(9) é falso)
- propagar esse “falso” através da cadeia, forçando r9c7(9) a ser verdadeiro
- r2c7 e r9c7 estão na mesma coluna, então ambos não podem ser 9 → contradição
Portanto, r2c7 não pode ser 9, e esse candidato vermelho pode ser eliminado.
Prática
Os três diagramas a seguir são todos cadeias de um dígito. Sem pressa.
Três perguntas rápidas de autoverificação:
- Quais segmentos são elos fortes e por que são “um ou outro”?
- Quais segmentos são elos fracos e por que são mutuamente exclusivos?
- Por que o candidato vermelho leva a uma contradição?
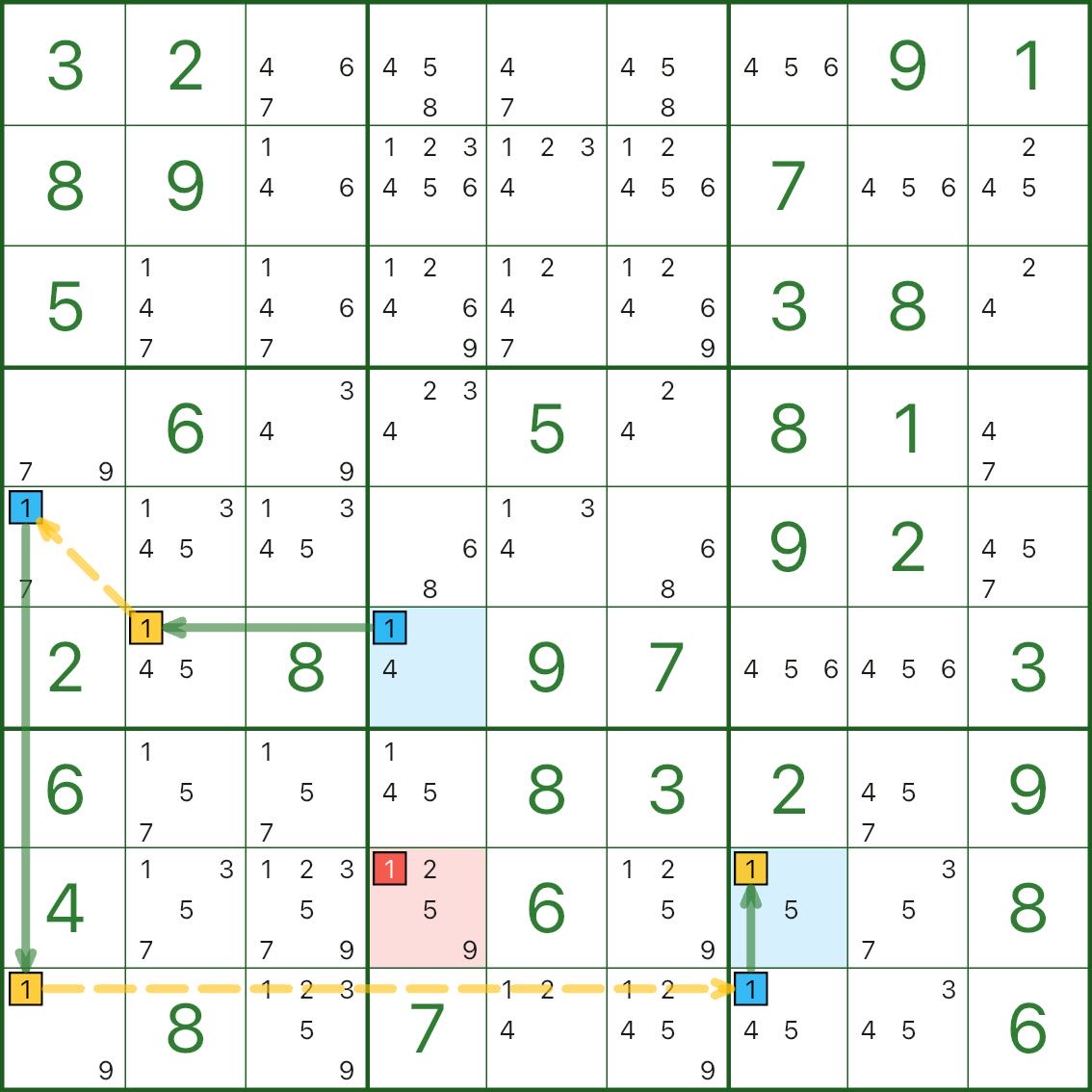
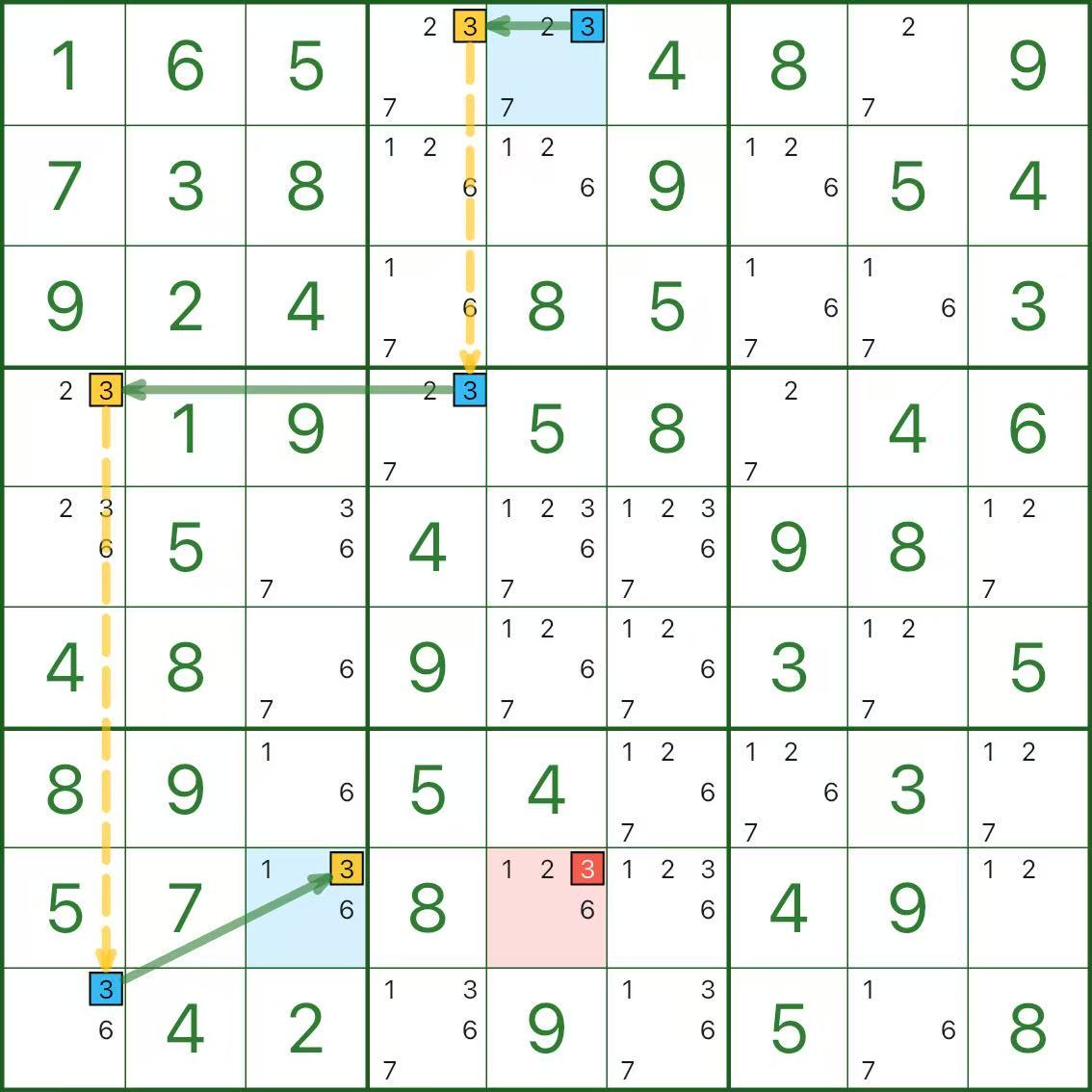
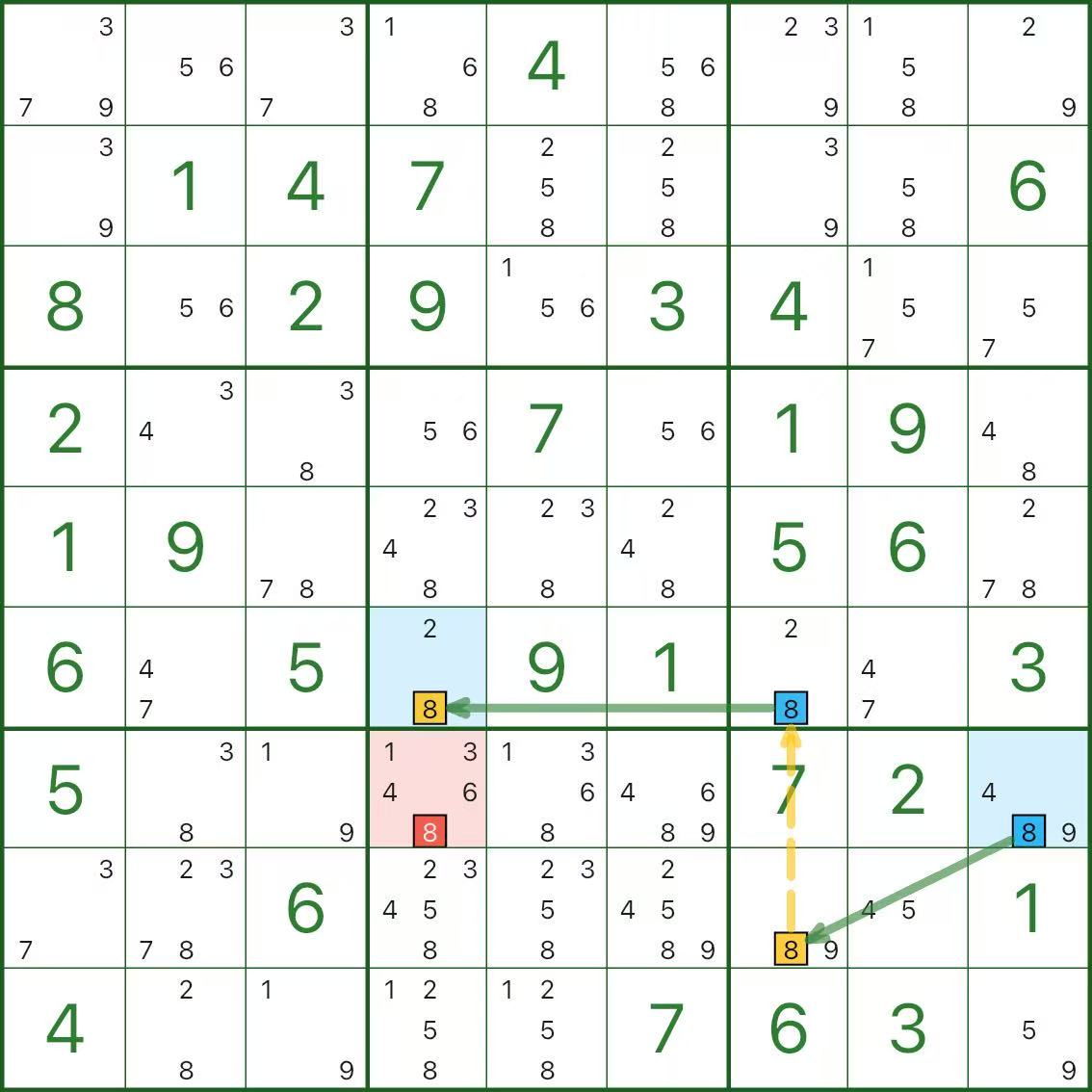
Se parecer um pouco tortuoso no início, isso é completamente normal.
Isso é uma cadeia: a base de muitas técnicas avançadas – sinta-se confortável com ela antes de prosseguir.