#ERRO+1

Pré-requisito: BUG+1 depende do quebra-cabeça ter exatamente uma solução.
Se você ainda não leu, comece aqui:
Uniqueness

---

1. Visão geral

BUG+1 é a abreviação de BUG + 1 — você também pode ouvi-lo chamado Bivalue Universal Grave + 1.

O nome parece assustador, mas descreve um estado muito específico do tabuleiro:

• quase todas as células não resolvidas são bivalores (exatamente 2 candidatos)
• uma “célula de exceção” tem 3 candidatos (esse é o “+1”)

O que é BUG?

BUG = Túmulo Universal Bivalor.

É chamado de “túmulo” porque a grade pode parecer “travada”: os candidatos vêm aos pares em todos os lugares e o progresso muitas vezes fica paralisado sem singularidade.

Quando a grade satisfaz essas duas condições, ela se torna uma estrutura “BUG” muito simétrica:

1. toda célula não resolvida é bivalor
2. para qualquer dígito d, em cada casa (linha/coluna/caixa), o número de posições candidatas para d é par
   • mais comumente 2
   • se d já estiver colocado naquela casa, pode ser 0 (ainda par)

Essa simetria geralmente permite duas conclusões válidas (múltiplas soluções).

Então o que é BUG+1?

BUG+1 é “quase um BUG, mas não exatamente”:

• todas as células não resolvidas são bivaloradas
  exceto uma célula com 3 candidatos

Esse candidato extra quebra a simetria uniforme – e é exatamente isso que nos permite forçar um posicionamento usando exclusividade.

Portanto, a célula de exceção tem um candidato forçado — podemos colocar o dígito diretamente.

---

2. Passo a passo

Etapa 1: identifique o estado “quase todos os bivalores” (imagem superior)

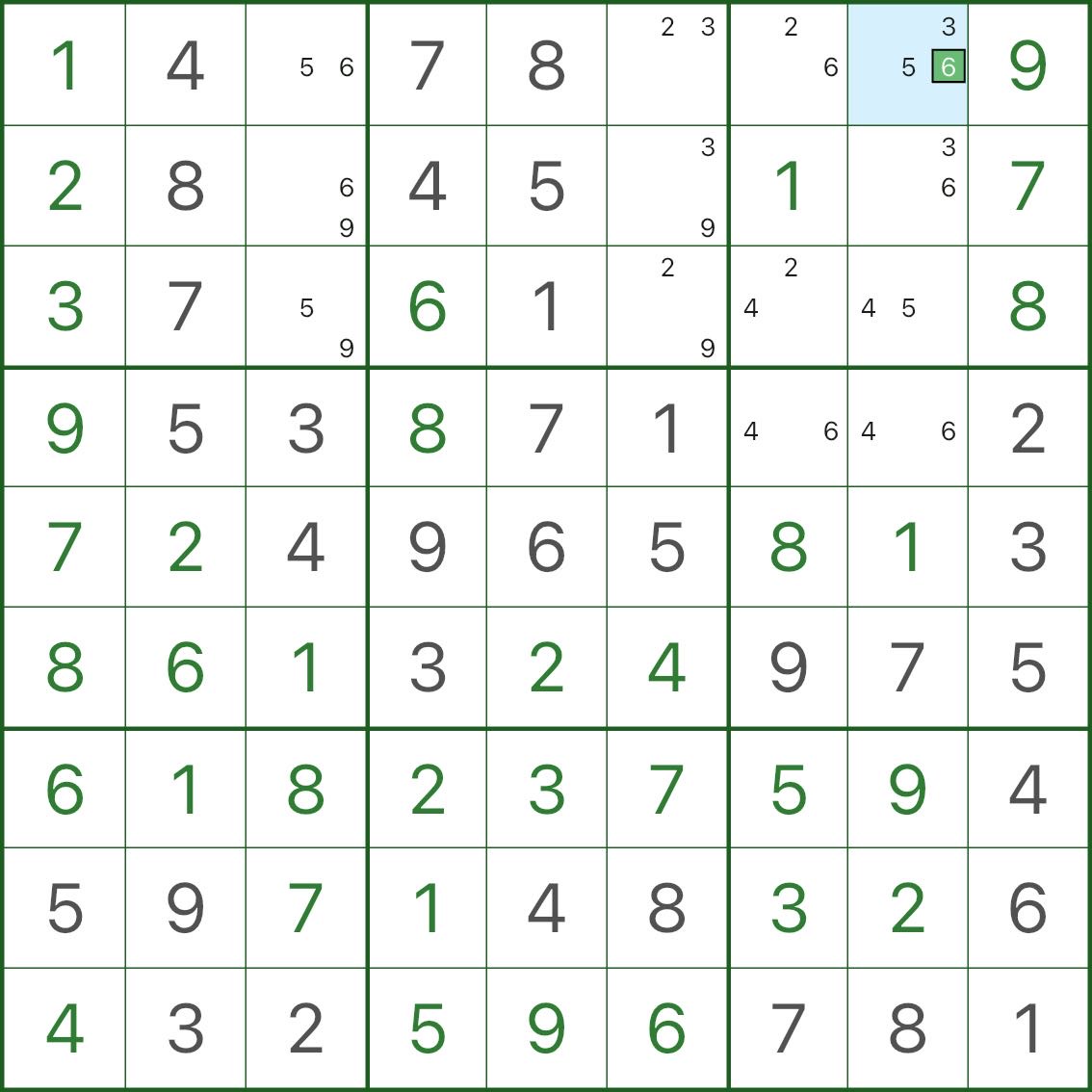
Na imagem:

• a maioria das células vazias mostra apenas 2 candidatos pequenos
• uma célula é a exceção, mostrando 3 candidatos (o “+1”)

Passo 2: qual dígito devemos colocar? (e por quê?)

Nós nos concentramos apenas nos três candidatos na célula de exceção e fazemos uma coisa simples: verificar ímpar vs par.

Como:

1. observe os três candidatos na célula de exceção
2. para cada um desses dígitos, conte quantas vezes ele aparece como candidato na célula de exceção linha/coluna/caixa

Normalmente, você descobrirá que um dígito aparece 3 vezes (ímpar) em uma dessas casas.
Esse candidato “ímpar” é o dígito que você deve colocar.

Por que? Use uma contradição:

Suponha que não coloquemos este candidato “ímpar” e, em vez disso, escolhamos um dos outros dois candidatos “pares”:

1. a célula de exceção torna-se bivalor
2. a distribuição de candidatos entre as casas retorna a uma simetria “par” (uma estrutura BUG)
3. As estruturas BUG geralmente permitem duas conclusões válidas (múltiplas soluções)

Mas o quebra-cabeça deve ser único, para que essa escolha seja impossível.
Portanto, o candidato “ímpar” deve ser verdadeiro – esse é o dígito que você coloca.

Se você não quiser contar nada: a dica irá destacar o candidato forçado para você.

---

3. Exemplo

A imagem abaixo mostra o resultado: o candidato “+1” forçado na célula de exceção é colocado.

---

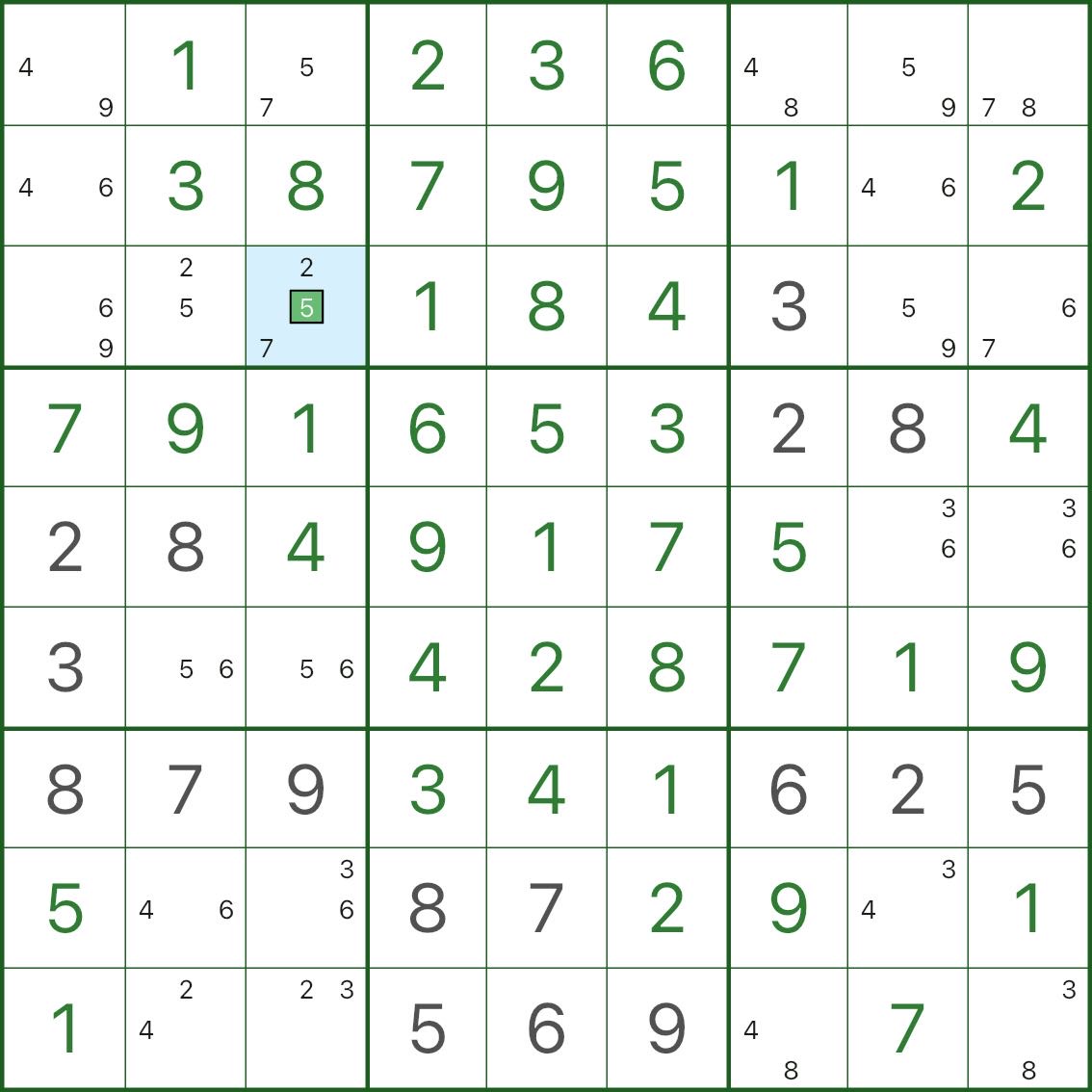
4. Como detectar BUG+1

Use esta lista de verificação:1) Certifique-se de que suas anotações de candidato estejam completas e confiáveis (gere candidatos completos, se necessário)
2) Procure uma grade onde:

• todas as células não resolvidas são bivaloradas
• exatamente uma célula tem 3 candidatos

3. Na linha/coluna/caixa dessa célula, conte as ocorrências candidatas para esses três dígitos: o ímpar (normalmente 3) é o dígito forçado
4. A dica irá destacar a célula de exceção e mostrar qual candidato é forçado

Nota: BUG+1 é uma técnica baseada em exclusividade — ela só se aplica quando é garantido que o quebra-cabeça tenha uma única solução.