XY-윙

설명

XY-Wing(Y-Wing이라고도 함)은 한 개의 피벗과 두 개의 날개로 구성된 짧은 후보 제거 체인입니다.

그 모양은 다음과 같습니다.

• 피벗(파란색): 정확히 2개의 후보 x, y
• 날개(노란색): {x, z} 및 {y, z}

결론: 두 날개를 모두 볼 수 있는 셀은 z를 포함할 수 없으므로 후보 z는 그곳에서 제거될 수 있습니다.

---

설명

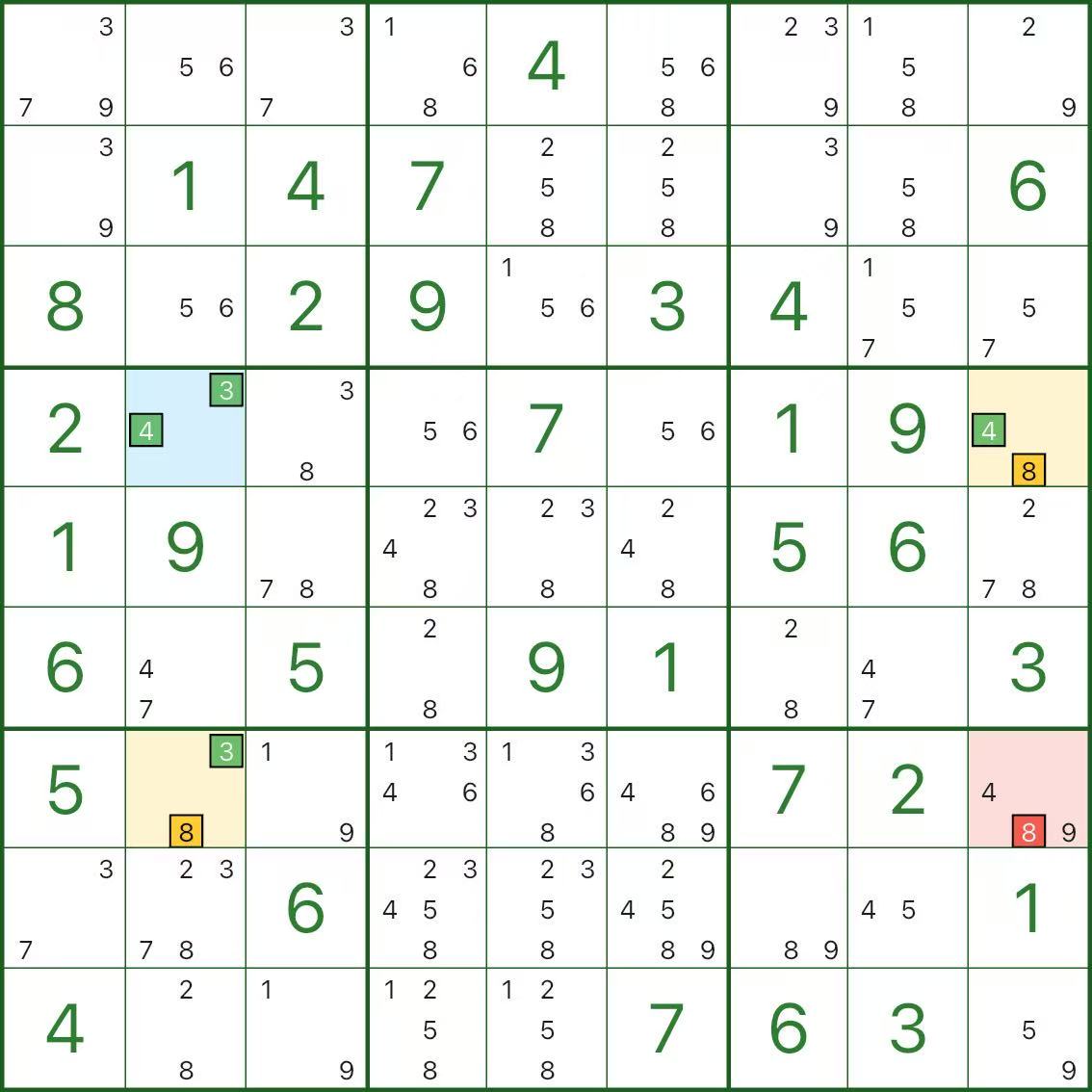
위 이미지에서는 r7c9(빨간색)의 후보 8을 제거하려고 합니다.
파란색 피벗은 r4c2이며 후보 3과 4가 있습니다.
두 개의 노란색 날개는 다음과 같습니다.

• r4c9: 후보 4 및 8
• r7c2: 후보 3 및 8

r7c9에서8을 제거할 수 있는 이유는 무엇입니까? 짧은 모순이면 충분합니다.

• r7c9 = 8이라고 가정합니다(빨간색 후보가 참임).
• r7c9는 양쪽 날개를 모두 볼 수 있으므로 양쪽 날개에서 8이 제거됩니다.
  • r4c9는 4여야 합니다.
  • r7c2는 3이어야 합니다.
• 이제 피벗 r4c2가 멈췄습니다.
  • r4c9 = 4 ⇒ r4c2는 4일 수 없습니다(같은 행).
  • r7c2 = 3 ⇒ r4c2는 3이 될 수 없습니다(같은 열).
  • r4c2에는 {3,4}만 있었습니다 ⇒ 적합한 값이 없음 (모순)

따라서 가정은 불가능합니다. r7c9는 8이 될 수 없으며 후보 8은 제거될 수 있습니다.

---

예

이 이미지는 더 많은 XY-Wing 패턴을 보여줍니다. 피벗(파란색) / 두 개의 날개(노란색) / 제거(빨간색)와 같은 동일한 구조를 찾아보세요.

---

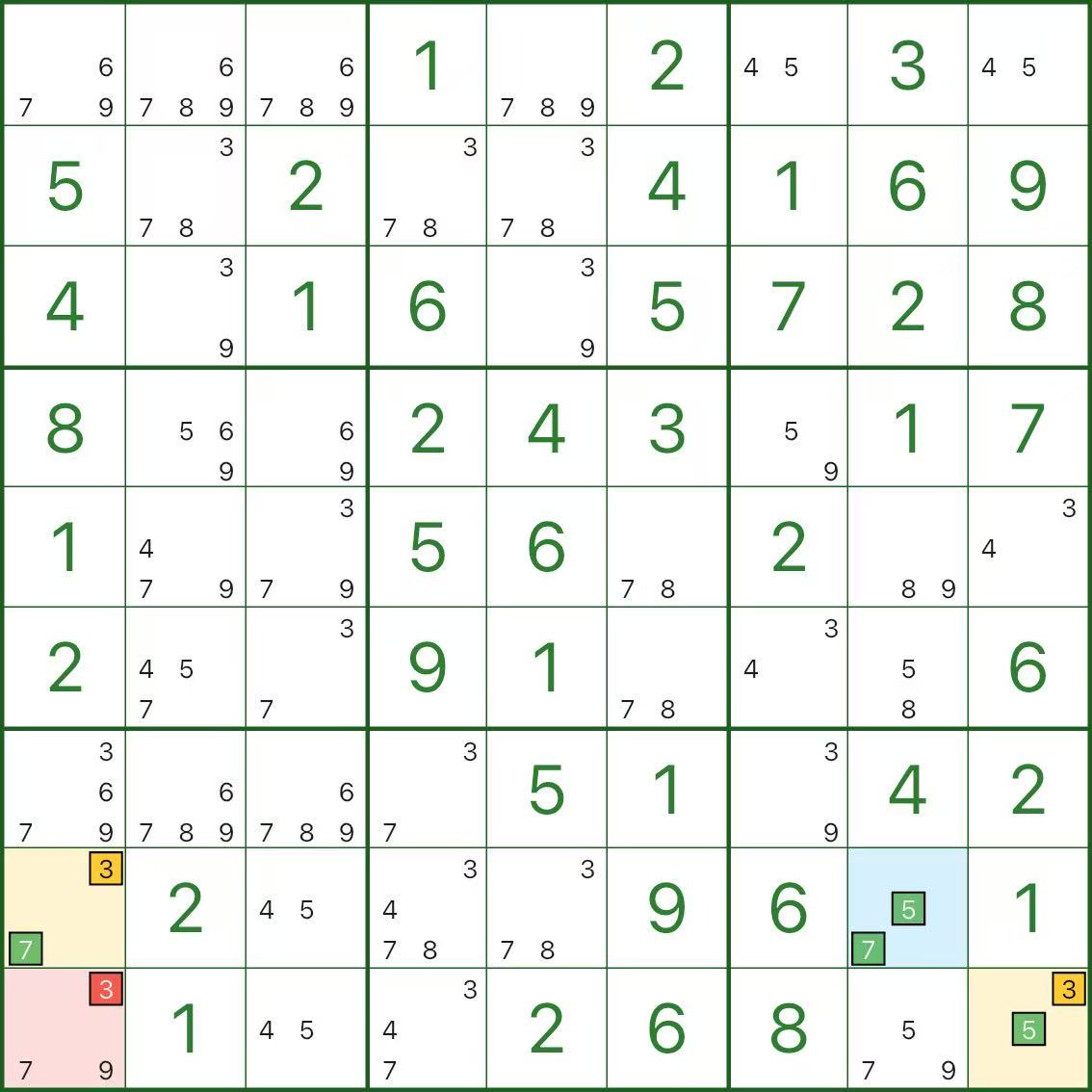
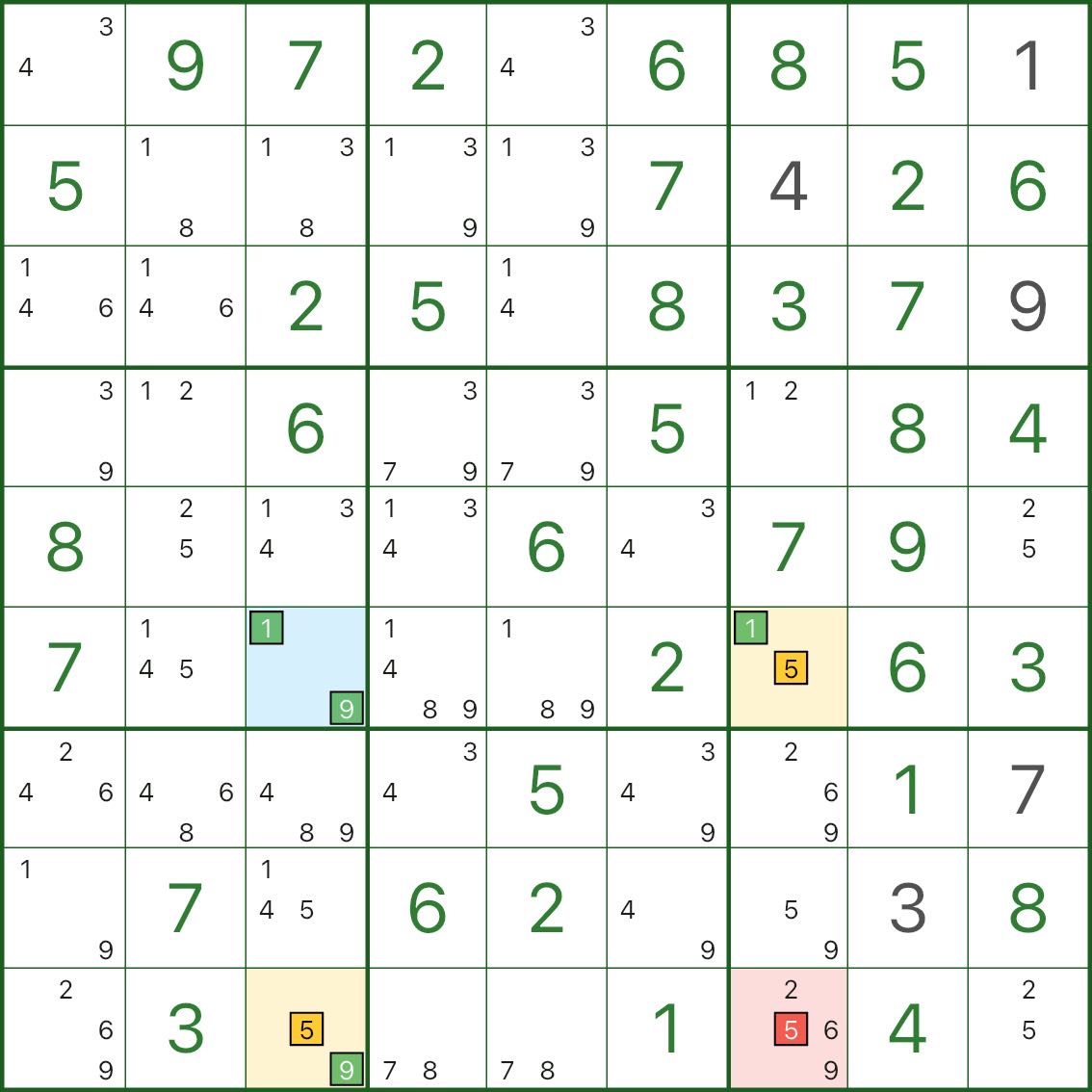
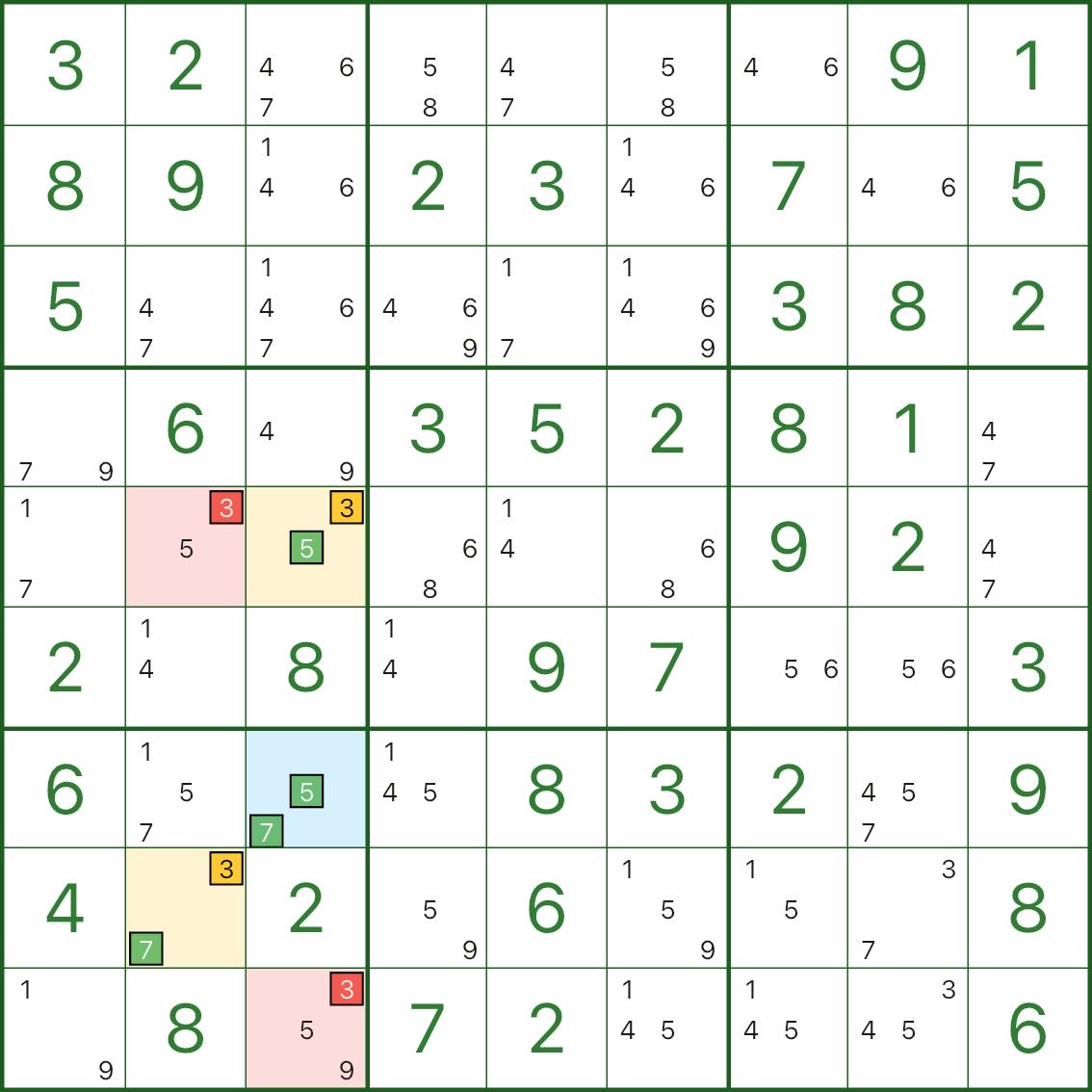
XY-Wing 찾는 방법

한 줄 체크리스트: 두 개의 후보 피벗 {x,y}를 찾고 두 개의 두 개의 후보 날개 {x,z} 및 {y,z}를 찾은 다음 두 날개를 보는 모든 셀에서 z를 제거합니다.

실제 퍼즐에서는:

1. 정확히 2개의 후보가 피벗(파란색)인 셀을 찾습니다.
2. 피벗을 볼 수 있는 두 개의 셀을 찾습니다. 각 셀에는 {x,z} 및 {y,z}(노란색) 모양의 정확히 두 개의 후보가 있습니다.
3. 두 날개를 볼 수 있는 셀은 일반적인 제거 지점입니다. 그곳에서 후보 z를 제거합니다(빨간색).