학습 문서 / 고유 직사각형(UR)
고유 직사각형(UR)
> 전제 조건: UR은 퍼즐에 <strong>정확히 하나의 솔루션</strong>이 있다는 사실에 의존합니다.
Intermediate
고유 직사각형(UR)
전제 조건: UR은 퍼즐에 정확히 하나의 솔루션이 있다는 사실에 의존합니다.
아직 읽지 않았다면 여기에서 시작하세요.
Uniqueness
1. 개요
UR(Unique Rectangle)은 단일 솔루션 속성을 사용하여 후보를 제거하고 때로는 숫자를 배치하는 기술 계열입니다.
"위험한 모양"에 중점을 둡니다.
- 4개의 셀이 2×2 직사각형을 형성합니다(2개의 행 × 2개의 열, 정확히 2개의 상자에 걸쳐 있음).
- 네 모서리 모두 동일한 두 개의 핵심 후보를 포함합니다(예: 1과 7).
4개의 셀에 해당 쌍만 남겨두면 직사각형이 두 가지 다른 방법(두 숫자를 교환하여)으로 채워지는 경우가 많아 고유성이 손상될 수 있습니다.
따라서 고유성 가정 하에서 일부 후보를 제거해야 하거나 셀이 특정 값을 취해야 한다는 결론을 내릴 수 있습니다.
2. 공략(5종)
아래 5개의 이미지는 5개의 일반적인 UR 유형에 해당합니다(앱 내 힌트에 유형 I~V로 표시됨).
색상 가이드:
- 파란색 셀: UR 직사각형(핵심 구조)
- 노란색 표시: 추론에서 중점을 두는 후보
- 빨간색 표시: 제거할 후보/또는 설정할 수 있는 셀
유형 I: 단일 지붕 → 강제 값
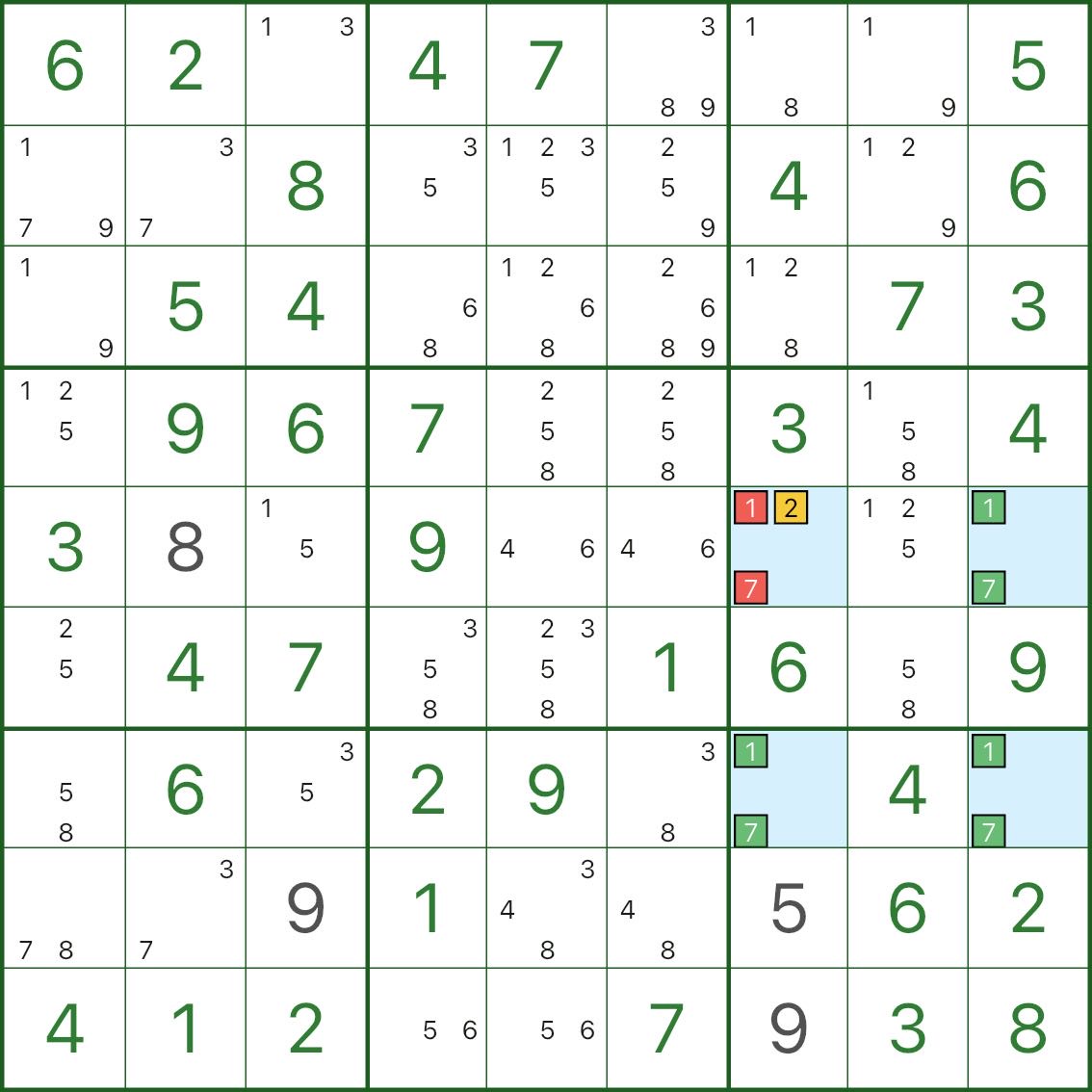
4개의 파란색 셀을 살펴보세요. 직사각형을 형성하고 모두 1 및 7 후보를 포함합니다.
셀 r5c7에는 추가 후보 2도 있습니다.
r5c7에서 2가 참가 아니면 r5c7에는 1과 7만 남게 됩니다.
이렇게 하면 네 모서리가 모두 "{1,7} 전용"이 되어 두 개의 교체 가능한 채우기가 허용됩니다(고유성을 깨뜨림).
따라서 고유성 하에서는 다음과 같습니다.
- r5c7은 후보 1과 7을 유지할 수 없습니다.
- 따라서 r5c7은 2여야 합니다
유형 II: 두 개의 지붕 → 두 지붕이 모두 보이는 c를 제거합니다.
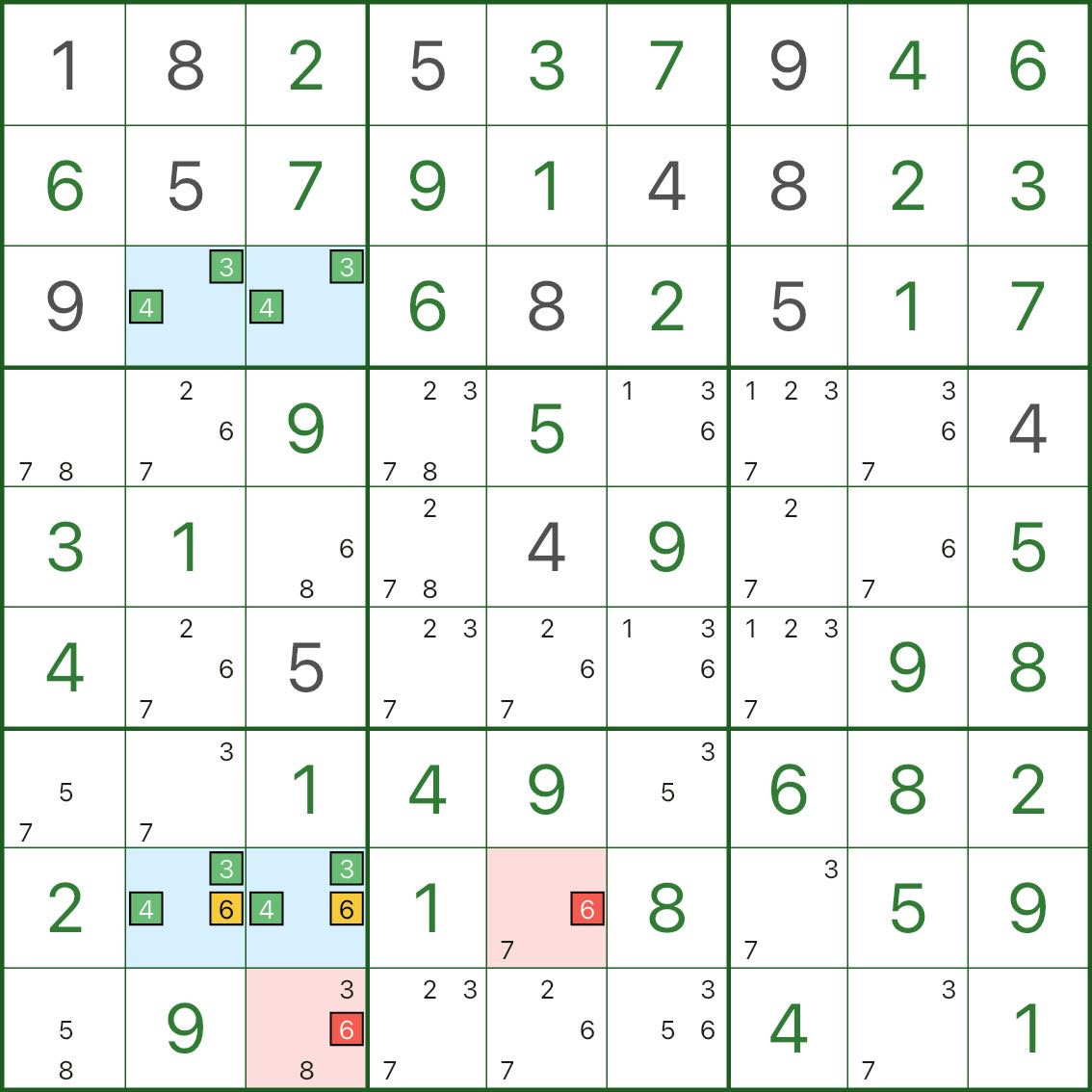
여기서 파란색 직사각형은 핵심 후보 3 및 4를 기반으로 합니다.
두 개의 파란색 셀 r8c2 및 r8c3에도 후보 6이 포함되어 있습니다(따라서 {3,4,6}입니다).
이제 두 가지 지붕 셀을 모두 볼 수 있는 빨간색 후보 6(예: r8c5 또는 r9c3)를 생각해 보세요.
- 빨간색 6이 사실이라면 두 지붕 모두 6이 아님이 강제됩니다.
- 지붕은 {3,4}로만 다시 무너집니다.
- 직사각형은 다시 치명적인 {3,4} 패턴이 됩니다(독창성을 깨뜨림).
따라서 해당 빨간색 6개 후보는 사실일 수 없으며 제거될 수 있습니다.
유형 III: 지붕을 "패키지"로 취급하고 하위 집합을 형성합니다.
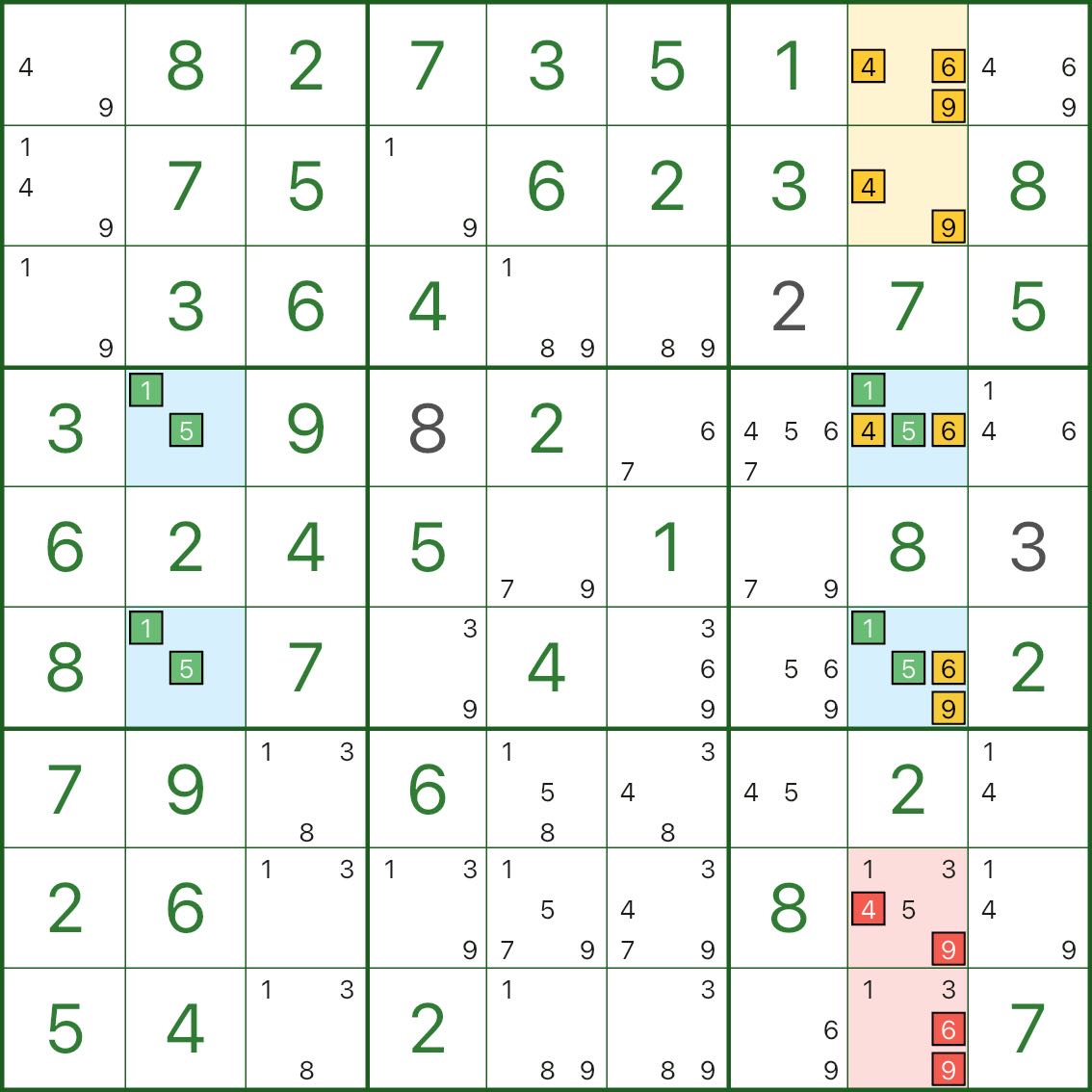
이것은 열 8에 중점을 둡니다.
- 8열의 두 파란색 셀에는 모두 핵심 후보 1 및 5가 포함되어 있습니다.
- 그들은 또한 추가 숫자 4, 6, 9를 공유합니다(따라서 각각은 {1,5,4,6,9}입니다)
고유성은 중요한 제약을 강제합니다.
- 두 개의 파란색 셀 중 적어도 하나는 {4,6,9}의 숫자를 가져와야 합니다.
- 그렇지 않으면 둘 다 {1,5}에만 의존하여 직사각형을 치명적인 패턴으로 바꿉니다.
따라서 "두 개의 파란색 셀의 추가 숫자 {4,6,9}"를 패키지로 처리할 수 있습니다.
노란색 셀 r1c8 및 r2c8과 함께 이는 열 8의 작은 하위 집합 내에서 숫자 4, 6, 9를 효과적으로 잠급니다.
따라서 8열(빨간색으로 표시)의 다른 4/6/9 후보는 제거될 수 있습니다.
IV 유형: 공액 쌍은 한 자리를 강제로 지정 → 다른 자리를 제거
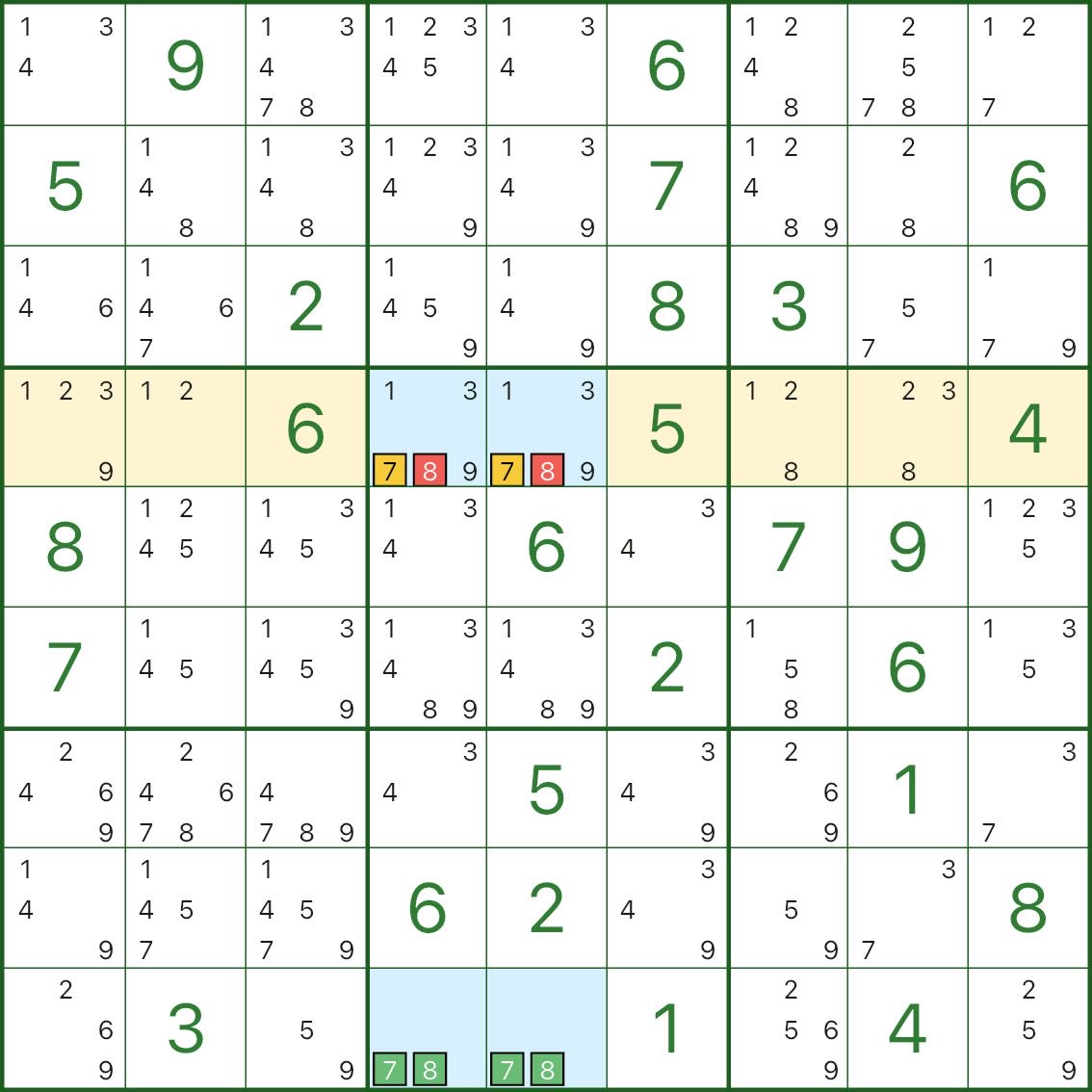
파란색 직사각형은 다시 코어 쌍(여기서는 7 및 8)에 구축됩니다.행 4에서 후보 7은 두 개의 파란색 셀 r4c4 및 r4c5에만 나타납니다.
이는 다음을 의미합니다.
- r4c4 / r4c5 중 하나는 7이어야 합니다.
이 제약 조건을 사용하면 후보 8을 동일한 파란색 셀에 유지하면 직사각형이 치명적인 구조로 붕괴될 수 있습니다(고유성을 깨뜨림).
따라서 r4c4 및 r4c5에서 8을 제거할 수 있습니다.
유형 V: 여러 개의 지붕(2 또는 3) → 모든 지붕 셀을 보는 c 제거
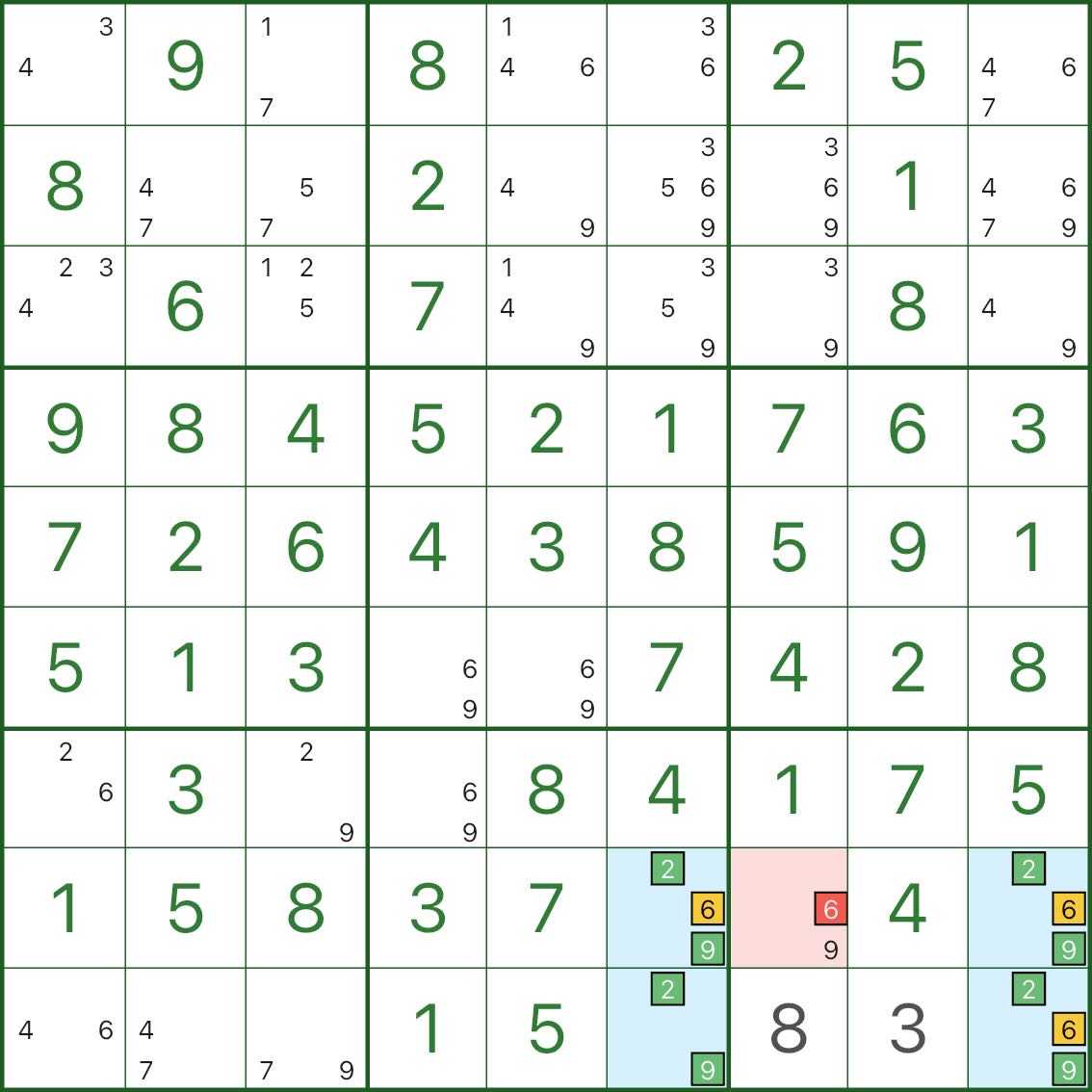
유형 V는 엄밀히 말하면 "세 개의 지붕"이 아닙니다. 핵심 아이디어는 다음과 같습니다.
- 직사각형에는 2~3개의 지붕 셀이 있으며 모두 동일한 추가 후보 c를 공유합니다.
- 2 지붕 셀만 있는 경우 일반적으로 동일한 행/열/상자를 공유하지 않습니다(공유하는 경우 유형 II에 더 가깝습니다)
- 셀의 후보 c가 지붕 셀 모두를 볼 수 있는 경우 해당 c는 참일 수 없으며 제거될 수 있습니다.
이 이미지에서 파란색 직사각형은 주로 숫자 2, 6, 9를 포함합니다.
- 세 개의 파란색 모서리는 {2,6,9}입니다.
- 남은 파란색 모서리는 {2,9}입니다(6개가 누락됨).
이제 빨간색 셀 r8c7을 살펴보세요. 후보 6이 있고 이 패턴의 {2,6,9} 지붕 셀 모두를 볼 수 있습니다.
r8c7 = 6인 경우:
- 세 개의 지붕 셀 모두 강제로 not-6이 됩니다.
- 그들은 {2,9}로만 축소됩니다.
- 직사각형은 치명적인 {2,9} 패턴이 됩니다(고유성을 깨뜨림).
따라서 r8c7의 후보 6은 참일 수 없으며 제거될 수 있습니다.
3. 예시
이 기사의 이미지 15는 이미 유형 IV의 예입니다.
연습할 때 먼저 파란색 직사각형을 찾은 다음 노란색/빨간색 표시를 위의 추론과 연결하세요.
4. 독특한 직사각형을 찾는 방법
실제 퍼즐에서는 다음 순서로 검색할 수 있습니다.
- 2×2 직사각형(2행 × 2열)을 형성하고 정확히 두 상자에 걸쳐 있는 빈 셀 4개를 찾습니다.
- 네 개의 코너가 모두 동일한 두 개의 핵심 후보("치명적인 쌍")를 공유하는지 확인합니다.
- 그런 다음 추가 후보의 모습을 기준으로 분류합니다.
- 한쪽 코너에만 추가 후보가 있음 → 유형 I(종종 강제 값)
- 두 모서리가 동일한 추가 숫자 c를 공유함 → 유형 II
- 지붕의 추가 숫자는 행/열/상자의 하위 집합을 형성할 수 있음 → 유형 III
- 집에서는 두 개의 직사각형 셀에만 핵심 숫자 1개가 나타남 → Type IV
- 두 개 또는 세 개의 모서리가 동일한 추가 숫자 c를 공유합니다(2개 지붕의 경우 일반적으로 집을 공유하지 않음) → 유형 V
한 문장으로 표현하면 다음과 같습니다. 직사각형이 치명적인 패턴으로 붕괴되는 것을 절대 허용하지 마십시오. 그렇지 않으면 고유성이 깨질 수 있습니다.