쌍 및 하위 집합

노출된/숨겨진 쌍 및 하위 집합

쌍과 부분 집합은 가장 유용한 "후보 제거" 기술 중 일부입니다. 이름은 다르지만 모두 같은 일을 합니다.

하나의 집(행/열/상자)에서 작은 셀 집합과 작은 숫자 집합이 서로 "슬롯을 예약"하므로 해당 숫자는 해당 집의 다른 곳에 나타날 수 없습니다.

전문용어를 외울 필요는 없습니다. 간단한 경험 법칙:

• Naked: 셀이 표시하는 것부터 시작합니다(이 셀에는 다음 숫자만 포함됩니다).
• 숨김: 숫자가 들어갈 수 있는 곳부터 시작합니다(이 숫자는 이 셀에만 들어갈 수 있습니다).

---

1. 네이키드 페어

같은 집에서 두 셀에 모두 동일한 두 후보만 포함되어 있는 경우(예: {a,b}), 네이키드 쌍이 있습니다.

이는 다음을 의미합니다.

• 한 셀은 a여야 하고, 다른 셀은 b여야 합니다(순서는 알 수 없음).
• 따라서 후보 a와 b는 그 집의 다른 모든 빈 셀에서 제거될 수 있습니다.

먼저 아래 이미지를 보십시오. 강조 표시된 상자 3과 두 개의 녹색 셀 r2c9 및 r3c9에 초점을 맞추세요.
{1,5}만 가능하다는 것을 알 수 있습니다.

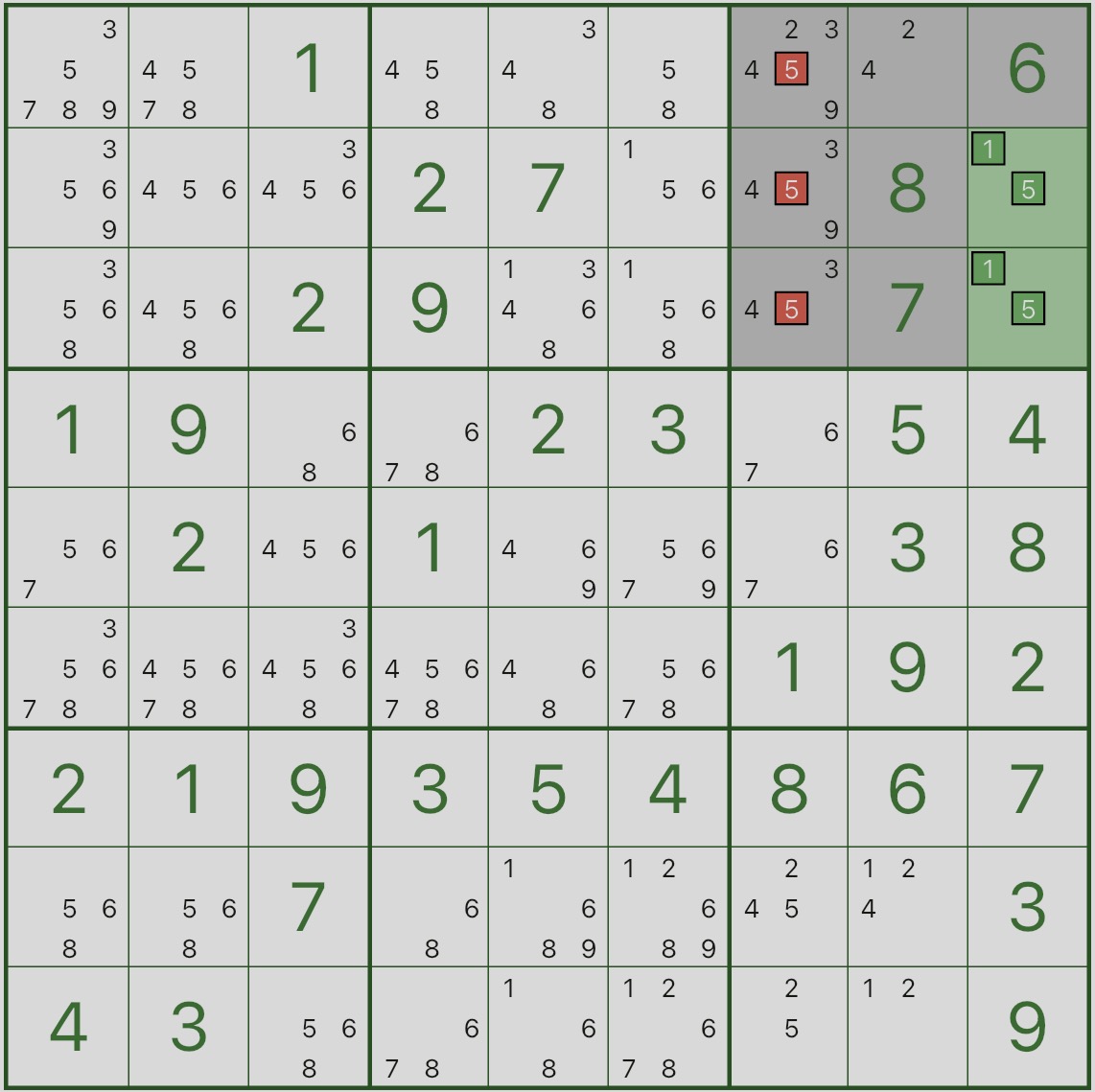
즉, 상자 3에서 숫자 1과 5는 r2c9 및 r3c9에 대해 "예약"되어 있습니다.

이제 빨간색 후보를 살펴보세요. r1c7, r2c7, r3c7의 후보 5를 제거할 수 있습니다.

모순에 의한 빠른 증명:

• r1c7은 5라고 가정합니다(r2c7 및 r3c7에도 동일한 논리가 적용됨).
• 그렇다면 상자 3에는 이미 5가 포함되어 있으므로 r2c9 및 r3c9는 5가 될 수 없으며 강제로 1이 됩니다.
• 그러나 r2c9와 r3c9는 동일한 열(열 9)을 공유하므로 둘 다 1일 수 없습니다. 모순
  ⇒ 해당 빨간색 5개 후보는 불가능하며 제거 가능

---

2. 숨겨진 쌍

같은 집에서 a 후보가 정확히 두 개의 셀에 나타나고 후보 b도 동일한 두 개의 셀에 나타나면 숨겨진 쌍이 있는 것입니다.

해당 두 셀에는 추가 후보가 표시될 수 있지만 a와 b는 이미 잠겨 있으므로 다음을 수행할 수 있습니다.

• 두 셀에서 a와 b를 제외한 모든 후보를 제거합니다.

먼저 아래 이미지를 보세요. 강조 표시된 열 4에 초점을 맞추세요.
해당 열에서 후보 4 및 5가 나타나는 위치를 찾으십시오. r1c4 및 r6c4에만 나타나는 것을 볼 수 있습니다.

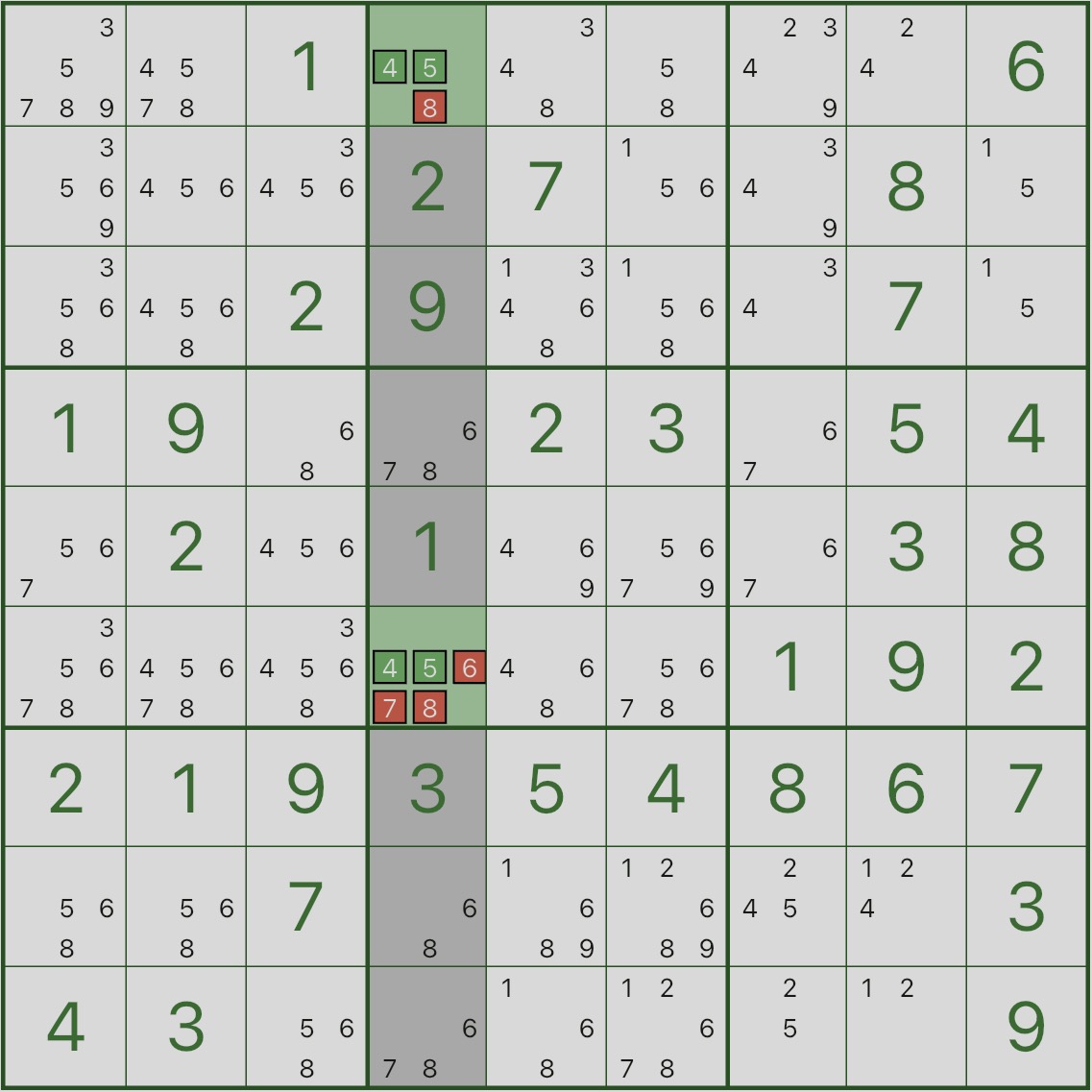
즉, 열 4에서 숫자 4 및 5는 r1c4 및 r6c4에 배치되어야 합니다.

r1c4 및 r6c4에서 다른 후보를 제거할 수 있는 이유는 무엇입니까?

• r1c4가 4나 5가 아닌 숫자를 취한다고 가정
• 그러면 4와 5는 모두 r6c4에만 적합해야 합니다.
• 하나의 셀은 4와 5가 동시에 될 수 없습니다 — 모순
  ⇒ r1c4 및 r6c4는 {4,5}여야 하므로 해당 셀의 다른 후보를 제거할 수 있습니다.

---

3. 네이키드 서브셋(트리플/쿼드)

이것은 일반화된 "알몸 쌍" 아이디어입니다.

집에 있는 N 셀에 집합적으로 N 숫자만 포함되어 있는 경우(예를 들어 세 개의 셀에 {a,b,c}만 포함), 네이키드 트리플이 있습니다. 동일한 아이디어가 쿼드에도 적용됩니다.

해당 숫자는 해당 N 셀 내에 배치되어야 하므로 다음과 같습니다.

• 그 집의 다른 모든 빈 셀에서 해당 숫자(예: a, b, c)를 제거합니다.

먼저 아래 이미지를 보십시오. 강조 표시된 행 8과 세 개의 셀 r8c1, r8c2, r8c4에 초점을 맞추세요.
이 세 개의 셀에는 총체적으로 {5,6,8}만 포함되어 있는 것을 알 수 있습니다.

즉, 8행에서 숫자 5, 6, 8은 r8c1, r8c2, r8c4 내에 배치되어야 합니다.

그렇기 때문에 나머지 8행의 빨간색 5, 6, 8 후보가 제거될 수 있습니다.

간단한 모순 견해:

• 행 8의 다른 셀이 {5,6,8} 중 하나를 "취하는" 경우
• 그러면 그 3개 셀은 3개 셀에 대해 2자리 숫자만 사용하여 채워야 합니다.
• 그건 안 돼요 - 모순

---

4. 숨겨진 하위 집합(트리플/쿼드)

이것은 일반화된 "숨겨진 쌍" 아이디어입니다.

집의 N 자리가 동일한 N 셀에만 나타나는 경우(해당 셀에 추가 후보가 포함된 경우에도) 숨겨진 트리플/쿼드가 있는 것입니다.

해당 N 자리는 해당 N 셀에 잠겨 있으므로 다음과 같습니다.

• 해당 셀에서 해당 N자리를 제외한 모든 후보를 제거합니다.

먼저 아래 이미지를 보세요. 강조 표시된 열 5에 초점을 맞추세요.
숫자 4,7,8은 r1c5, r8c5, r9c5에만 나타납니다.

이는 열 5에서 숫자 4, 7, 8이 r1c5, r8c5, r9c5 내에 배치되어야 함을 의미합니다.

따라서 이 세 셀에서 4, 7, 8이 아닌 다른 후보를 제거할 수 있습니다.

그게 왜 안전한가요?

• 이 셀 중 하나라도 다른 숫자를 사용하는 경우
• 그렇다면 4, 7, 8은 들어갈 수 있는 자리가 3개 미만이 됩니다 — 모순

---

5. 더 빨리 발견하는 팁

• 후보를 합리적으로 완전하게 유지하세요(더 어려운 퍼즐을 풀려면 후보가 필요합니다).
• 먼저 노출된 패턴을 스캔합니다. 후보가 거의 없는 셀(2, 3 또는 4)에서 시작합니다.
• 그런 다음 숨겨진 패턴을 검색하세요. 집에서 숫자가 2, 3, 4자리로 제한되어 있는지 확인하세요.
• 제거 후에는 잠시 멈추고 다시 살펴보십시오. 단순화된 후보는 종종 다음 단계를 드러냅니다.