3D 메두사 (고급 컬러링)

전제조건: Basic Coloring

개요

3D Medusa는 "업그레이드된 색상" 기술입니다. 상호 배타적인 두 가지 추론 경로를 나타내기 위해 여전히 두 가지 색상(파란색/노란색)을 사용하지만 더 이상 단 하나의 숫자에만 초점을 맞추지 않고 여러 숫자를 하나의 추론 네트워크에 연결할 수 있습니다.

이를 더욱 강력하게 만드는 것은 두 가지 이상의 강력한 링크를 사용한다는 것입니다.

• 공액 쌍(강한 링크): 행/열/상자에서 숫자는 정확히 2개의 후보 위치를 갖습니다.
• 이중 값 셀(강한 링크): 셀에는 정확히 2개의 후보가 있습니다.

강한 링크를 따라 색칠한 후에는 파란색/노란색을 두 가지 반대 가정으로 생각할 수 있습니다.

• 파란색이 참이라고 가정 ⇒ 노란색은 거짓
• 파란색은 거짓이라고 가정 ⇒ 노란색은 참입니다.

따라서 동일한 색상의 구성요소 내에서는 두 색상 중 하나가 참이어야 합니다.

3D Medusa는 가장 일반적으로 두 가지 종류의 결론을 제공합니다.

1. 트랩: 빨간색 후보가 파란색 경로와 노란색 경로 모두와 충돌 → 빨간색 후보 제거
2. 동색모순: 한 집(또는 셀)에서 두 개의 동일한 색상 후보가 충돌 → 전체 색상이 불가능하고 제거될 수 있음

아직 강한/약한 링크가 불편하다면 Chain Basics을 읽어보세요.

---

트랩

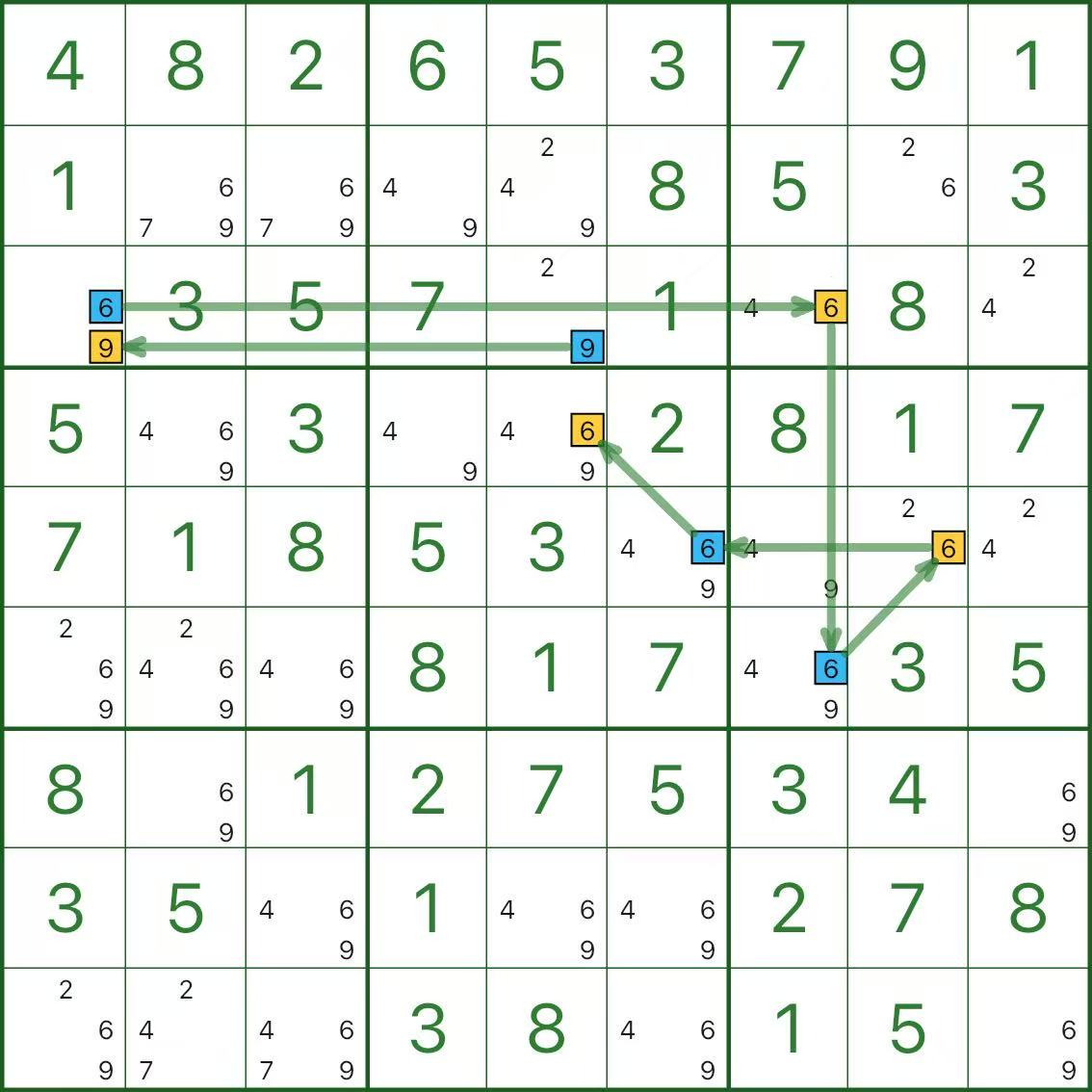
위 이미지에서는 강력한 링크를 따라 후보에 색상을 지정합니다. 체인에는 r3c5(파란색)의 후보 9가 포함되며 r4c5(노란색)의 후보 6에도 도달합니다.

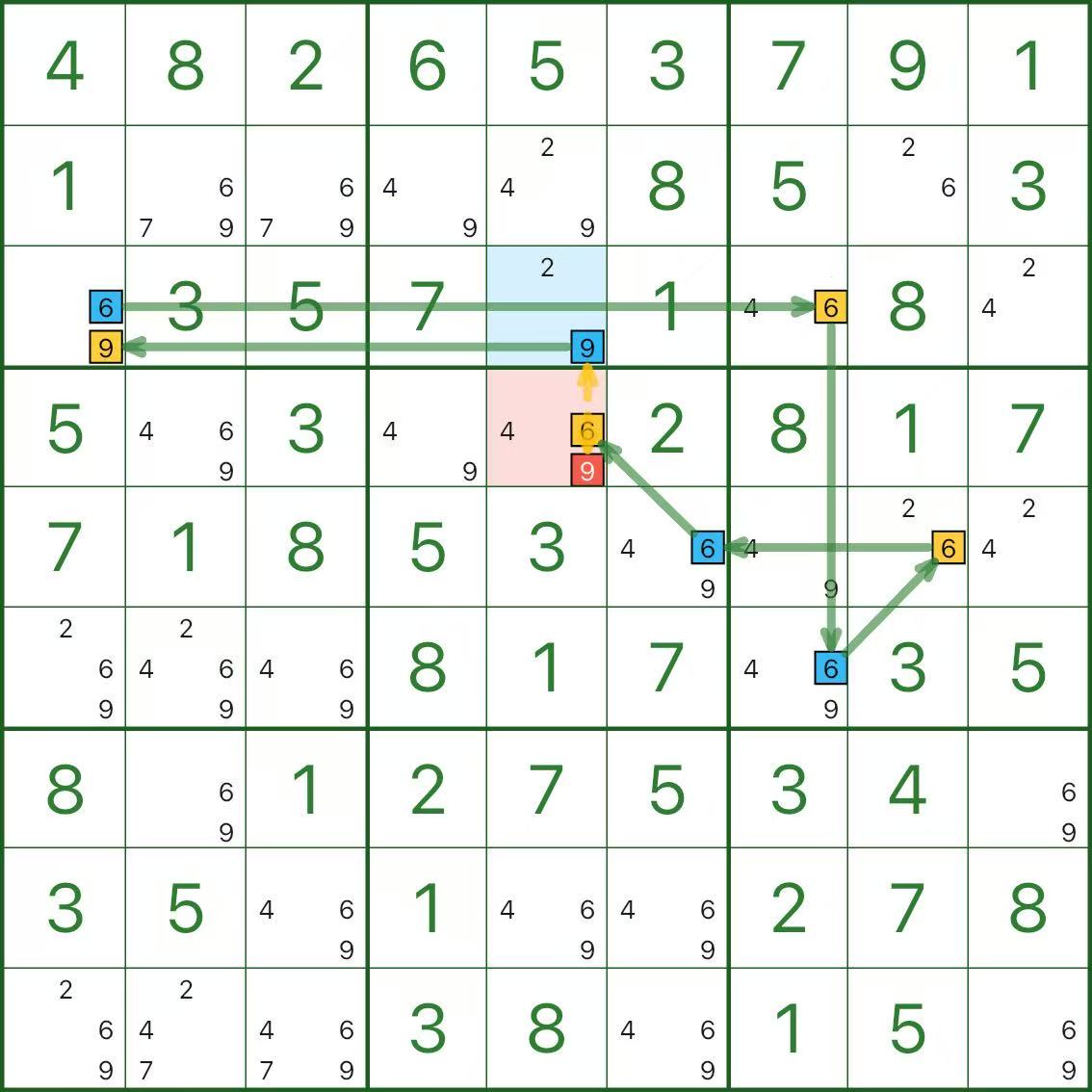
위 이미지에서 제거할 빨간색 후보는 r4c5의 후보 9입니다.
왜 제거할 수 있나요? 핵심 아이디어는 "두 가지 색상 중 하나가 참이어야 합니다"입니다.

• 파란색이 참이면 r3c5의 파란색 후보 9가 참이므로, r4c5의 빨간색 후보 9는 충돌하여 참일 수 없습니다.
• 파란색이 거짓이면 노란색 경로가 참이어야 합니다. r4c5의 후보 6(노란색)이 참이면 같은 셀의 9는 불가능하므로, r4c5의 빨간색 후보 9 역시 참일 수 없습니다.

어느 쪽이든 빨간색 후보는 불가능하므로 제거할 수 있습니다.

---

동색모순

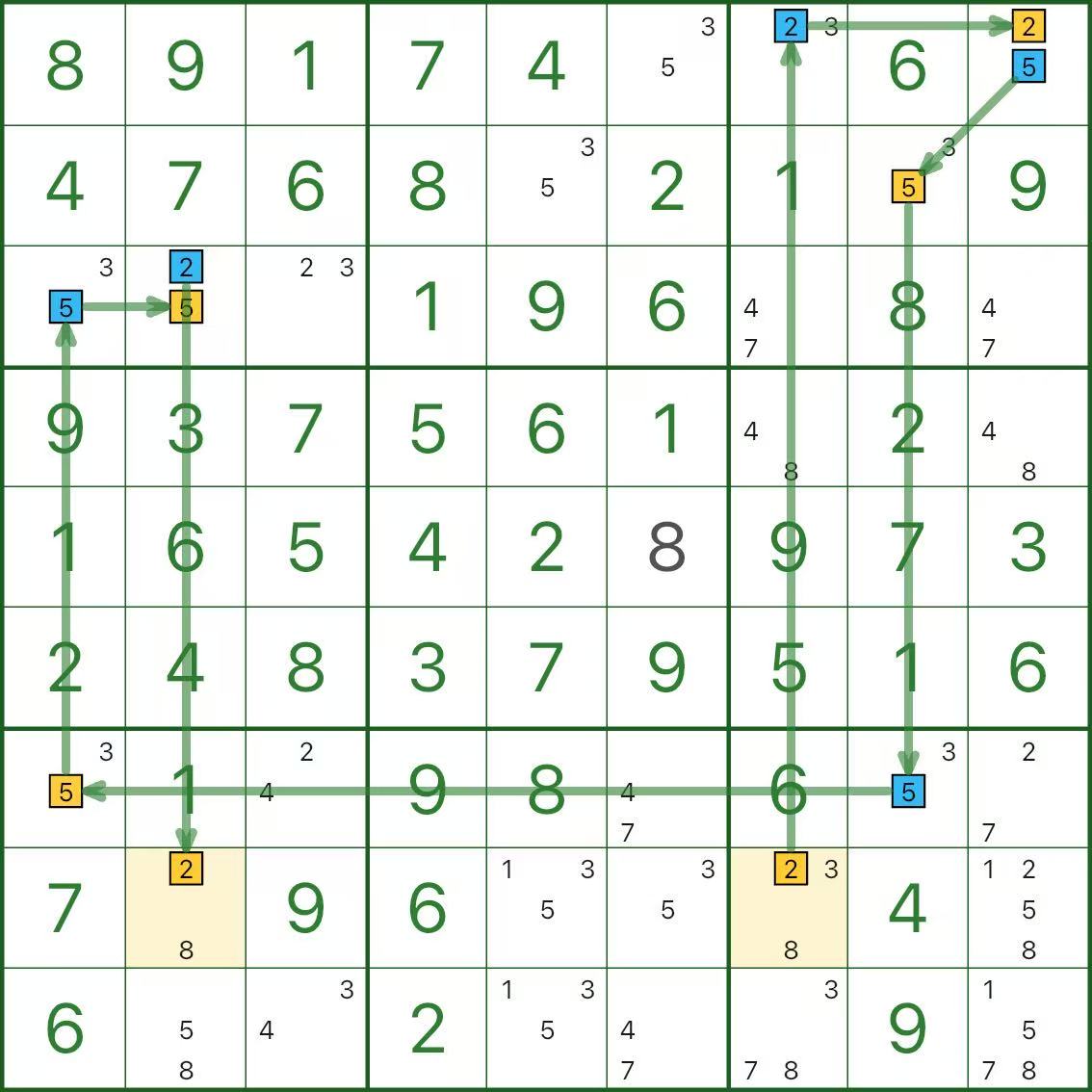
위 이미지에서 r8c2의 후보 2와 r8c7의 후보 2는 모두 노란색으로 표시됩니다.
하지만 같은 줄에 있으므로 둘 다 2가 될 수는 없습니다. 이는 동색 모순입니다.

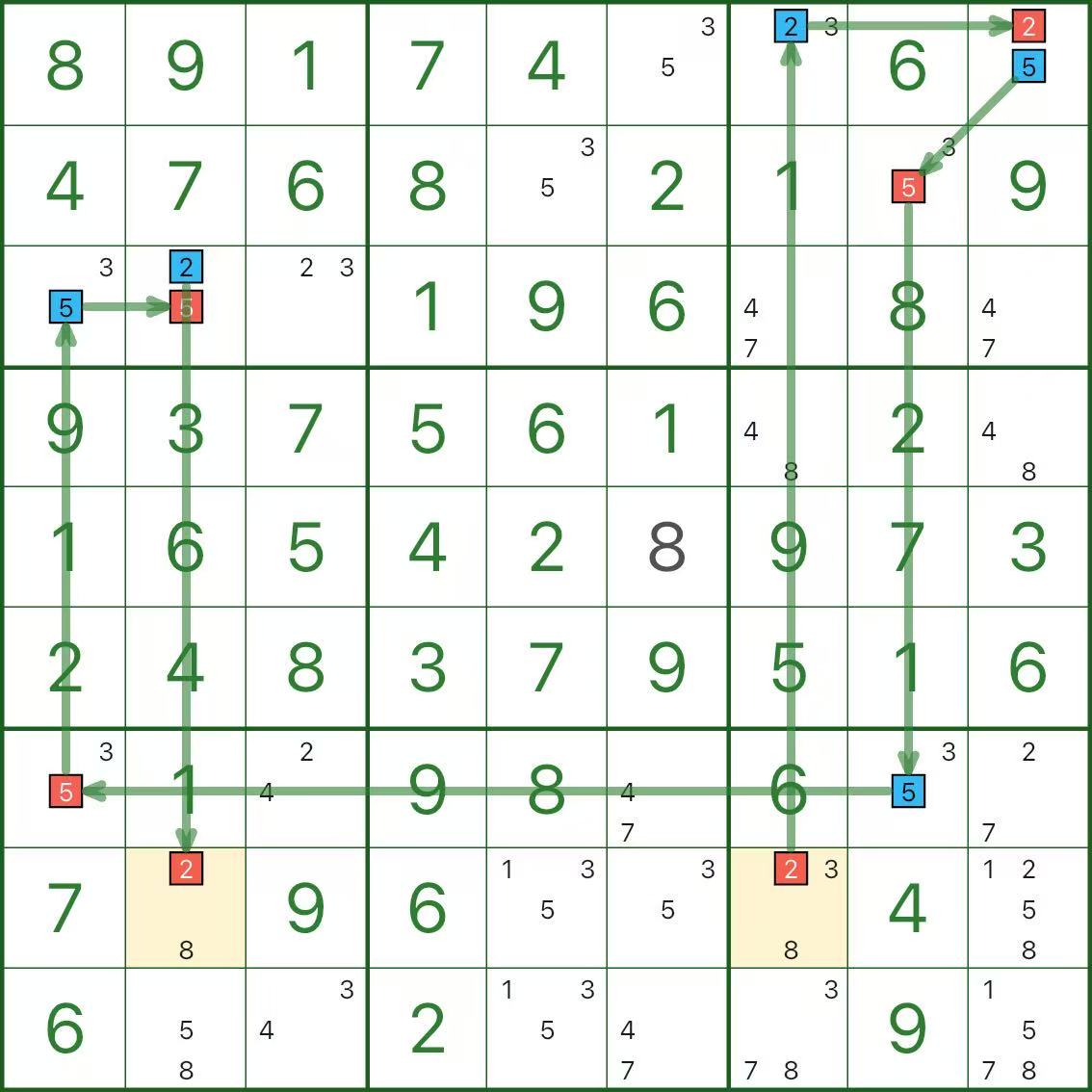
따라서 노란색 경로는 불가능하며 해당 색상 구성요소의 모든 노란색 후보는 제거될 수 있습니다(이미지에서 빨간색으로 표시됨).

---

3D 메두사 찾는 방법

한 줄 체크리스트: 강력한 링크 네트워크(켤레 쌍 + 이중값 셀)를 구축하고 파란색/노란색으로 색칠한 다음 함정이나 동색 모순을 찾습니다.

실제 퍼즐에서는:

1. 접합쌍과 이중값 셀에서 강력한 연결 찾기
2. 강한 링크에 따른 색상 후보(파란색/노란색은 상호 배타적임)
3. 다음을 찾으십시오:
   • 두 가지 색상 경로 모두와 충돌하는 빨간색 후보 → 함정 제거
   • 행/열/상자(또는 셀)에서 충돌하는 두 개의 동일한 색상 후보 → 해당 전체 색상 제거