기본 컬러링

전제조건: Chain Basics

설명

기본 색칠은 한 자리 후보 제거 기술입니다. 한 자리 d에 초점을 맞추고 이중 위치의 강력한 링크(자리 d가 정확히 두 개의 후보 셀에 나타나는 행/열/상자)만 사용합니다.

두 가지 색상(파란색/노란색)을 사용하여 강력한 링크를 따라 후보를 "채색"합니다.
이 두 가지 색상은 두 개의 상호 배타적인 추론 경로를 나타냅니다. 즉, 강한 연결에서는 정확히 한쪽 끝이 참이므로 색상이 번갈아 나타납니다.

하나의 색상 체인에서 파란색/노란색은 두 가지 반대 가정으로 생각할 수 있습니다.

• 파란색이 참이라고 가정 ⇒ 노란색은 거짓
• 파란색은 거짓이라고 가정 ⇒ 노란색은 참입니다.

따라서 동일한 강력한 링크에서는 두 색상 중 하나가 참이어야 합니다.

기본 색상 지정은 일반적으로 두 가지 결론으로 이어집니다.

1. 함정: 빨간색 후보는 파란색 후보 1개, 노란색 후보 1개를 볼 수 있음 → 빨간색 후보는 제거 가능
2. 동색모순: 한 집에 같은 색상의 후보 2명이 등장 → 전체 색상이 불가능하고 제거 가능

---

트랩

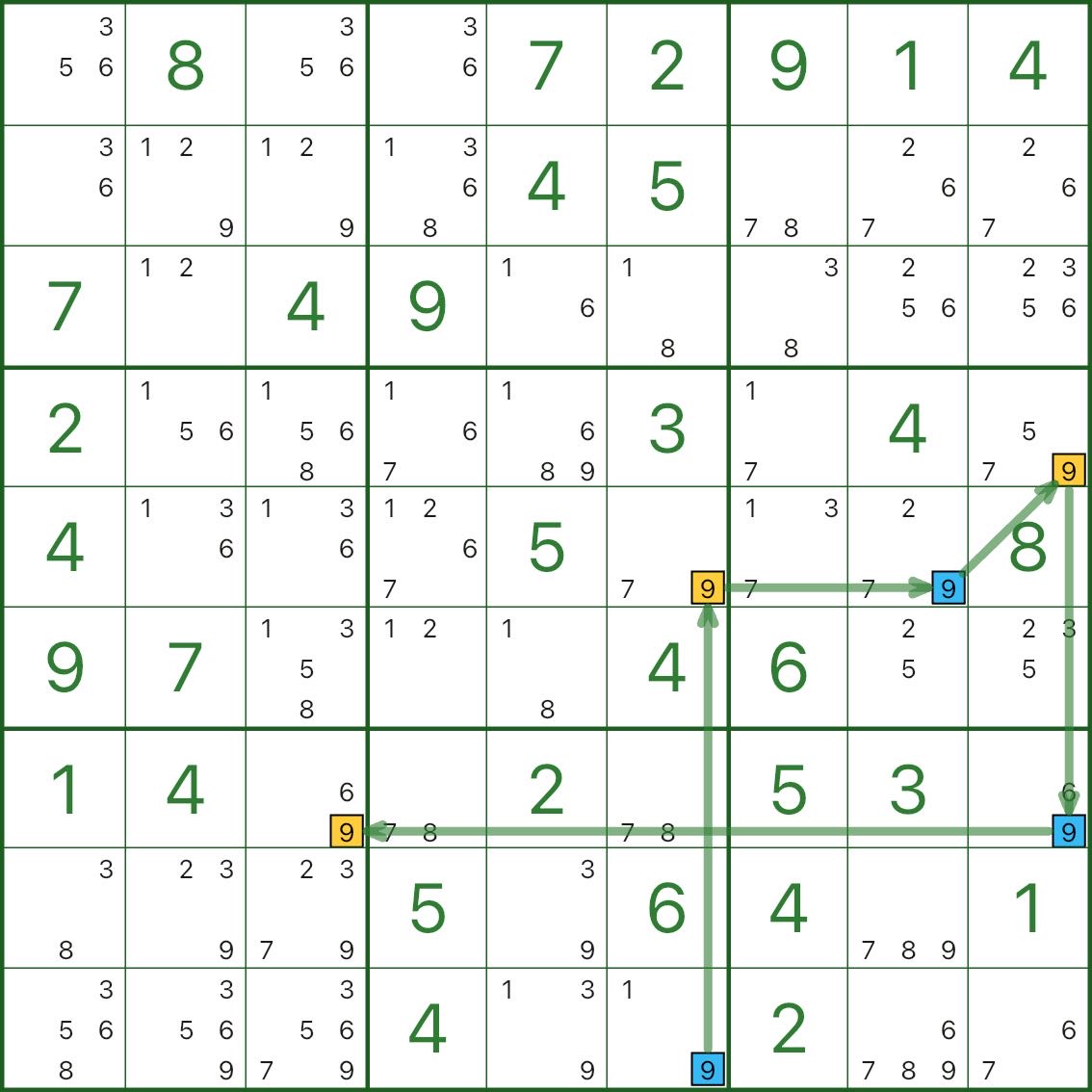
이미지 1에서 대상 숫자는 9입니다. r9c6부터 시작하는 강력한 링크 체인에 색상을 지정합니다. 다른 끝점은 r7c3(파란색/노란색)입니다.

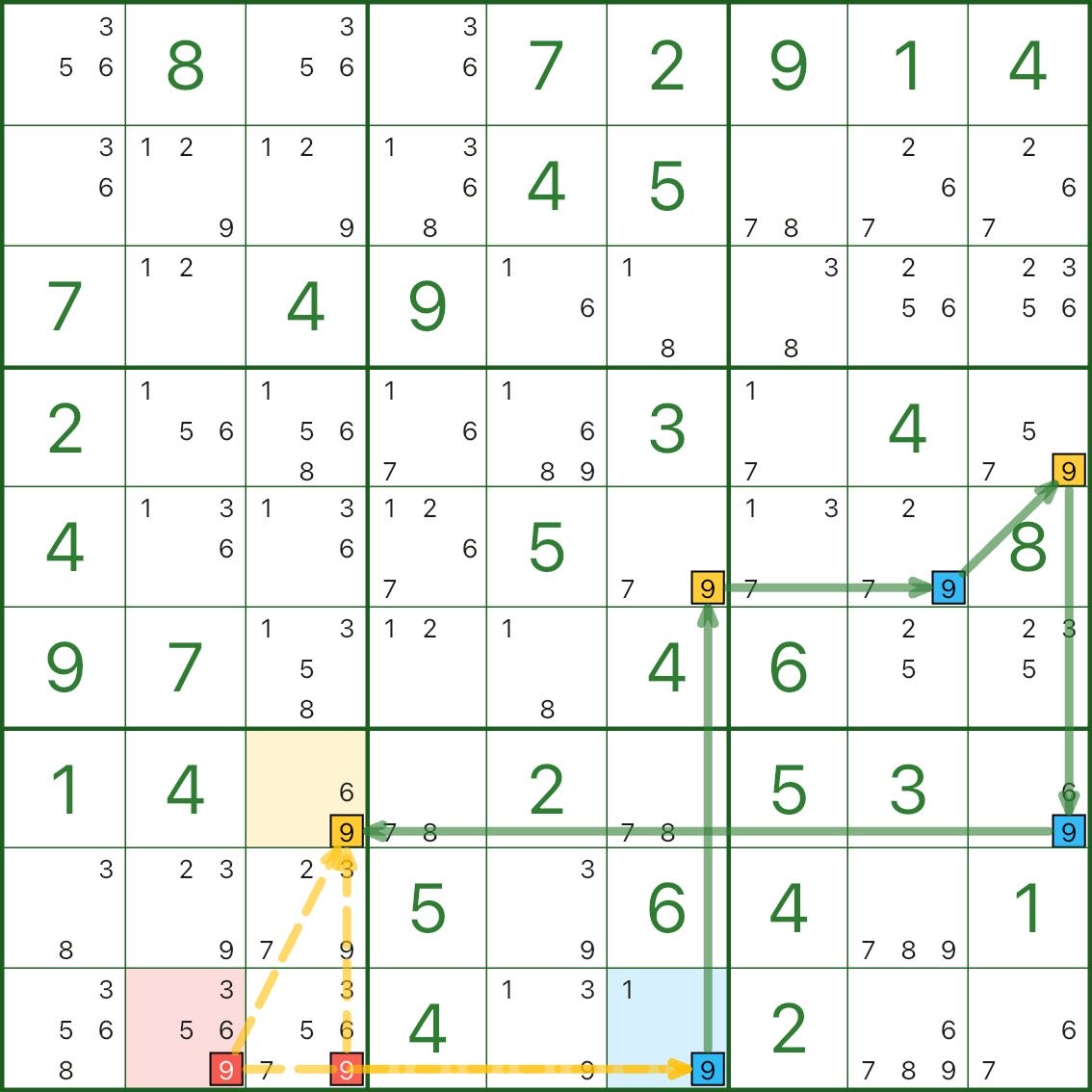
이미지 2에서 빨간색 후보는 r9c2의 후보 9 및 r9c3의 후보 9입니다.
왜 제거할 수 있나요? 핵심 아이디어는 다음과 같습니다.

• 파란색이 참인 경우 파란색 끝점(예: r9c6)은 9입니다. 빨간색 후보는 이를 볼 수 있으므로 파란색 끝점과 충돌하며 9가 될 수 없습니다.
• 파란색이 거짓인 경우 동일한 강력한 링크에서 노란색 끝점이 참이어야 합니다(예: r7c3은 9). 빨간색 후보도 볼 수 있으므로 여전히 충돌하며 9가 될 수 없습니다.

어느 쪽이든 빨간색 후보는 9가 될 수 없으므로 탈락할 수 있습니다.

---

동색모순

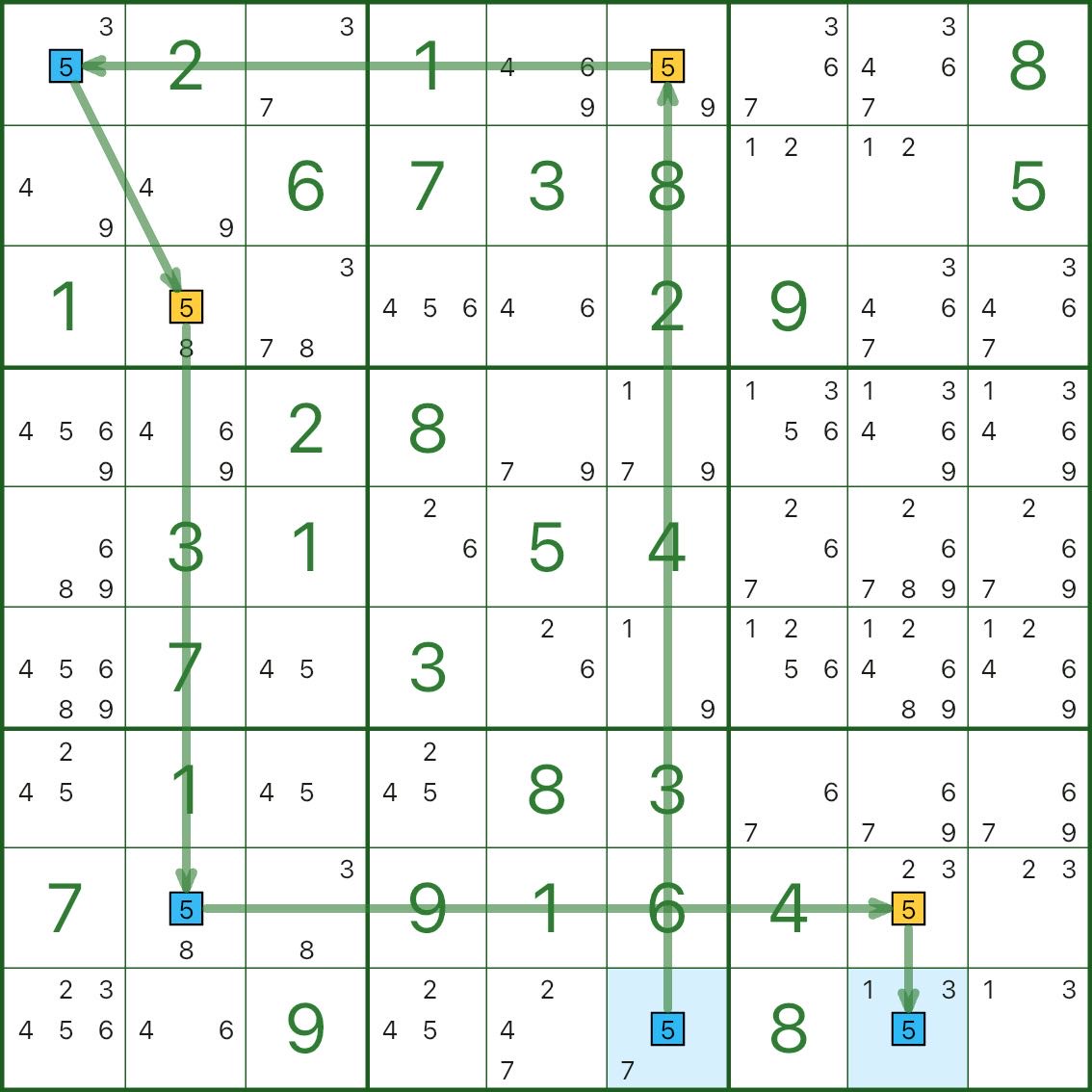
이미지 3에서 목표 숫자는 5입니다. r9c6부터 시작하여 체인은 결국 r9c8도 파란색 5가 되도록 강제합니다.
하지만 r9c6과 r9c8은 같은 행에 있으므로 둘 다 5가 될 수는 없습니다. 이는 동색 모순입니다.

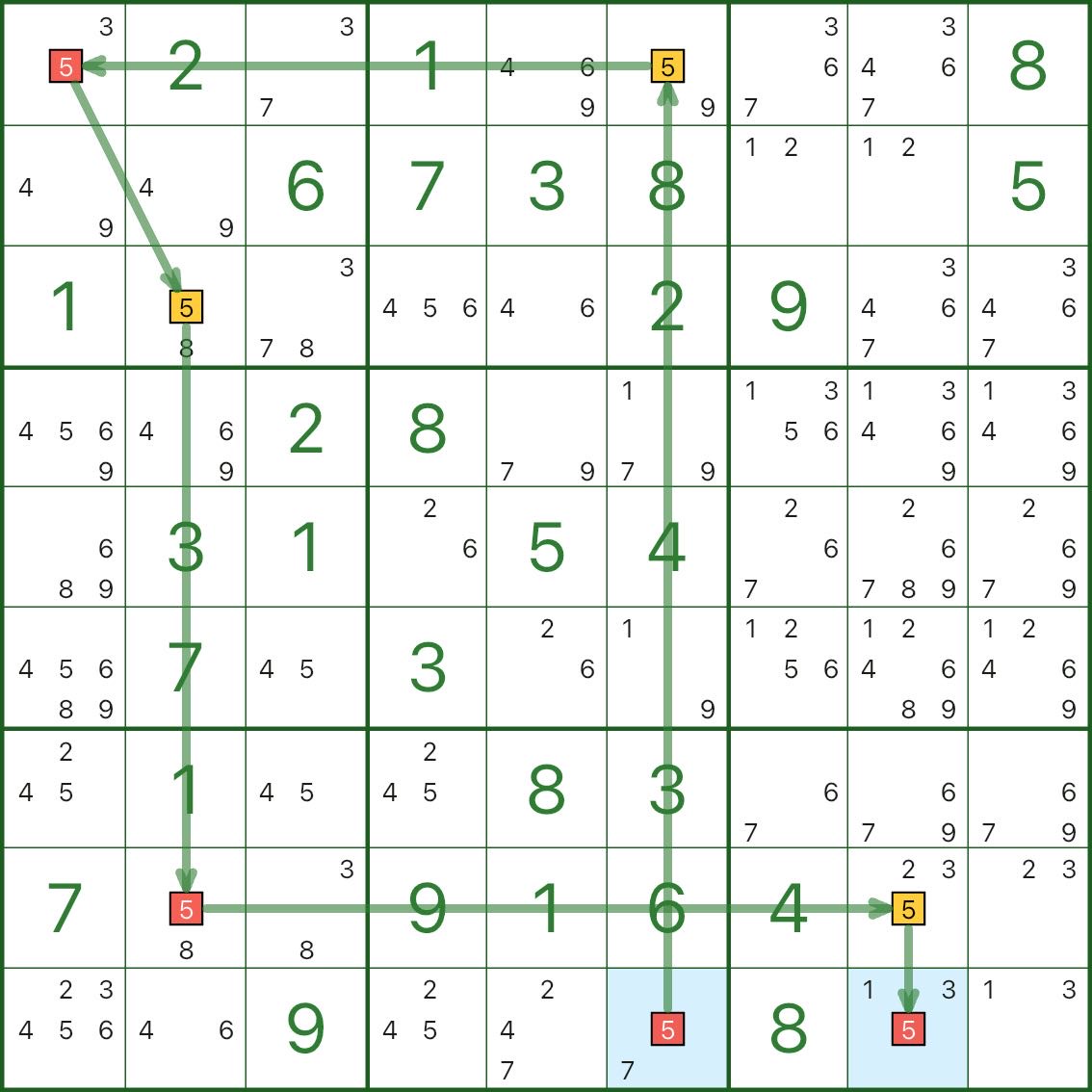
따라서 파란색 경로는 불가능합니다.
파란색 후보 5는 모두 제거될 수 있습니다(이미지 4 참조).

---

기본 컬러링 찾는 방법

한 줄 체크리스트: 강력한 이중 위치 링크를 찾아 파란색/노란색으로 색칠한 다음 함정이나 동색 모순을 찾습니다.

실제 퍼즐에서는:

1. 숫자 d를 선택하세요
2. d(d의 후보가 정확히 2개 있는 단위)에 대한 이중 위치 강력한 링크를 찾습니다.
3. 어디서든 시작하고 강력한 링크를 따라 색상을 바꿔보세요.
4. 다음을 찾으십시오:
   • 하나의 파란색과 하나의 노란색이 보이는 빨간색 후보 → 함정 제거
   • 하나의 유닛에 두 개의 동일한 색상 후보 → 해당 색상 전체를 제거