학습 문서 / 버그+1
버그+1
> 전제조건: BUG+1은 <strong>정확히 하나의 솔루션</strong>이 있는 퍼즐에 의존합니다.
Advanced
버그+1
전제조건: BUG+1은 정확히 하나의 솔루션이 있는 퍼즐에 의존합니다.
아직 읽지 않았다면 여기에서 시작하세요.
Uniqueness
1. 개요
BUG+1은 BUG + 1의 약어입니다. Bivalue Universal Grave + 1이라고도 들을 수 있습니다.
이름이 무섭게 들리지만 매우 구체적인 보드 상태를 설명합니다.
- 거의 모든 미해결 셀은 이중값입니다(정확히 2개의 후보).
- 하나의 "예외 셀"에는 3개의 후보가 있습니다(즉, “+1”).
버그란 무엇인가요?
BUG = 이중 가치 유니버설 무덤.
그리드가 "고착"된 것처럼 느껴질 수 있기 때문에 "무덤"이라고 부릅니다. 후보는 어디에서나 쌍으로 오고 진행은 종종 고유성 없이 중단됩니다.
그리드가 이 두 가지 조건을 만족하면 매우 대칭적인 "BUG" 구조가 됩니다.
- 모든 미해결 셀은 이중 값입니다.
- 모든 숫자 d에 대해 모든 집(행/열/상자)에서 d에 대한 후보 위치 수는 짝수입니다.
- 가장 일반적으로 2
- d가 이미 해당 하우스에 배치된 경우 0(여전히 짝수)일 수 있습니다.
이러한 대칭은 종종 두 가지 유효한 완성(다중 솔루션)을 허용합니다.
그렇다면 BUG+1은 무엇일까요?
BUG+1은 "거의 버그이지만 완전히는 아닙니다"입니다.
- 모든 미해결 셀은 이중값입니다.
3명의 후보가 있는 셀 1개만 제외
추가 후보는 균등한 대칭을 깨뜨립니다. 이것이 바로 고유성을 사용하여 배치를 강제할 수 있는 이유입니다.
따라서 예외 셀에는 하나의 강제 후보가 있습니다. 숫자를 직접 배치할 수 있습니다.
2. 연습
1단계: '거의 모든 이중값' 상태 확인(상단 이미지)
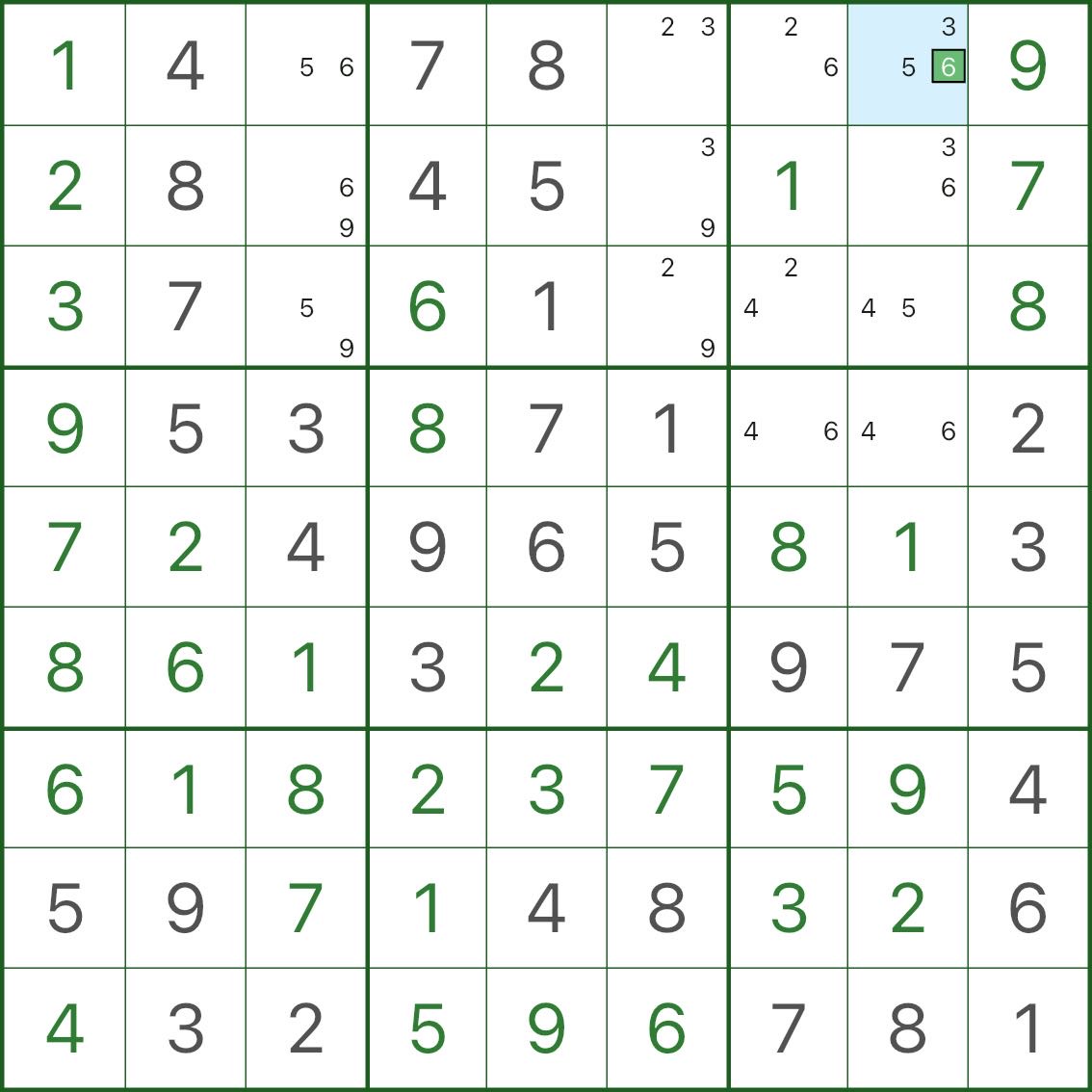
이미지에서:
- 대부분의 빈 셀에는 2개의 작은 후보만 표시됩니다.
- 하나의 셀은 예외이며 3 후보("+1")를 표시합니다.
2단계: 어떤 숫자를 놓아야 할까요? (그리고 왜?)
예외 셀의 3개 후보에만 초점을 맞추고 홀수 대 짝수를 확인하는 간단한 작업을 수행합니다.
방법:
- 예외 셀에 있는 세 후보를 살펴봅니다.
- 각 숫자에 대해 예외 셀의 행/열/상자에 후보로 나타나는 횟수를 세어보세요.
일반적으로 해당 집 중 하나에서는 한 숫자가 3번(홀수) 나타나는 것을 볼 수 있습니다.
그 "이상한" 후보는 당신이 놓아야 할 숫자입니다.
왜? 모순을 사용하세요:
이 "홀수" 후보를 배치하지 않고 대신 다른 두 개의 "짝수" 후보 중 하나를 선택한다고 가정합니다.
- 예외 셀이 이중값이 됩니다.
- 주택 전체의 후보 분포가 "균등한" 대칭(BUG 구조)으로 돌아갑니다.
- BUG 구조는 종종 두 가지 유효한 완성(다중 솔루션)을 허용합니다.
하지만 퍼즐은 고유해야 하므로 선택이 불가능합니다.
따라서 "홀수" 후보는 참이어야 합니다. 이것이 당신이 입력한 숫자입니다.
아무것도 계산하지 않으려면 힌트가 강제 후보를 강조 표시합니다.
3. 예시
아래 이미지는 결과를 보여줍니다. 예외 셀에 강제된 "+1" 후보가 배치됩니다.
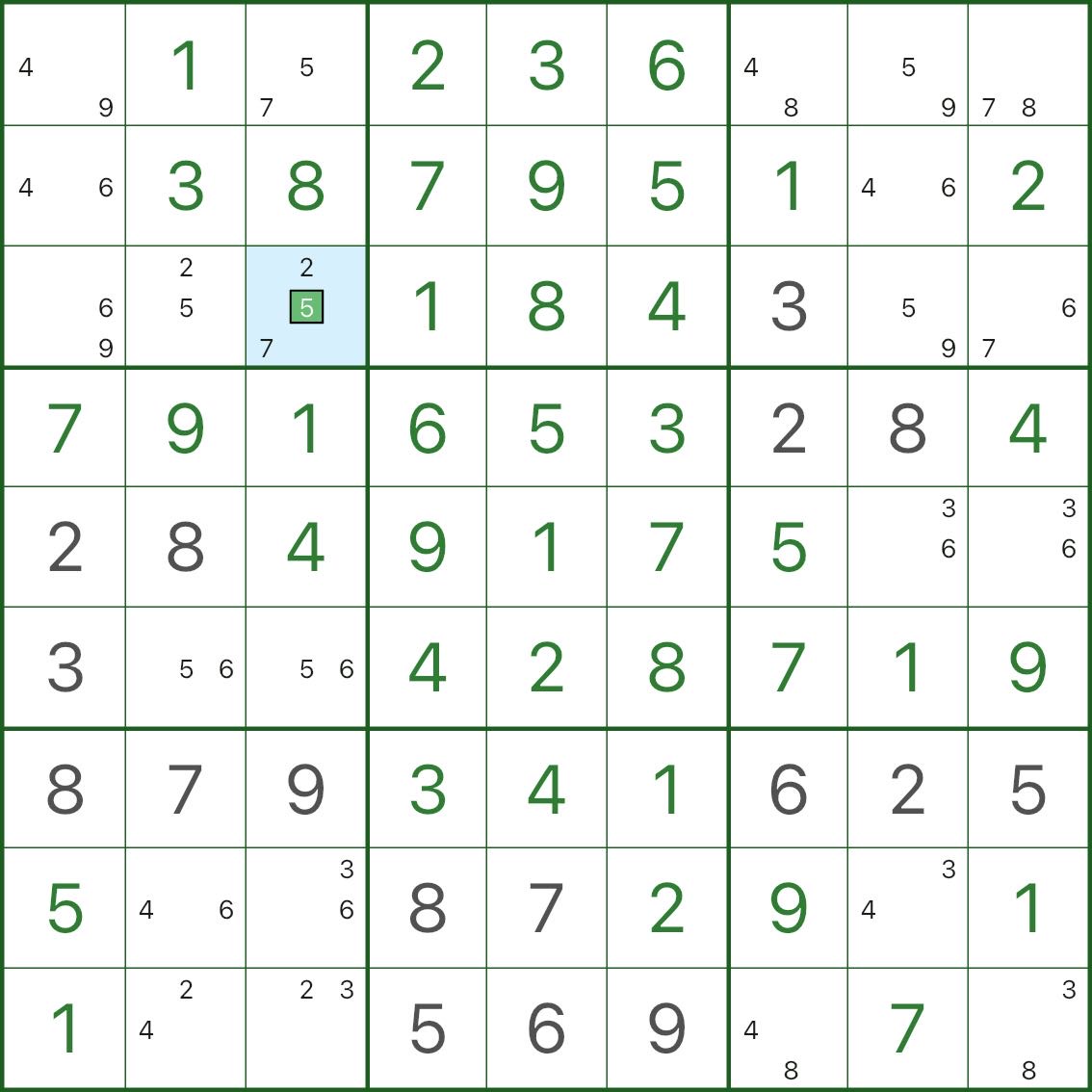
4. BUG+1 발견 방법
다음 체크리스트를 사용하세요:1) 후보 노트가 완전하고 신뢰할 수 있는지 확인하십시오(필요한 경우 전체 후보 생성). 2) 다음과 같은 그리드를 찾으세요.
- 모든 미해결 셀은 이중값입니다.
- 정확히 하나의 셀에는 3개의 후보가 있습니다.
- 해당 셀의 행/열/상자에서 해당 세 자리 숫자에 대한 후보 발생 횟수를 계산합니다. 홀수 1(일반적으로 3)은 강제 숫자입니다.
- 힌트는 예외 셀을 강조 표시하고 어떤 후보가 강제로 적용되는지 보여줍니다.
참고: BUG+1은 고유성 기반 기술입니다. 이는 퍼즐에 단일 솔루션이 보장되는 경우에만 적용됩니다.