#WXYZ-ウィング

これらをすでに読んでいる場合は、WXYZ-Wing がはるかに簡単に感じられるでしょう。
XY-Wing / XYZ-Wing

---

1. 概要

WXYZ-Wing は基本的に XY-Wing / XYZ-Wing の「大きい」バージョンです。小さな構造を使用して明確な矛盾を強制し、候補を排除します。

ボード上では通常、小さな色のクラスター (青いハブ セル + 黄色のウィング セル) のように見えます。

• このクラスター内のすべての候補は 4 桁に制限されています (例: {1,4,7,9})
• 赤色の候補 d が真であると仮定すると、クラスター内の他の場所から d が削除されます。
• この場合、クラスターには 4 つのセルを埋めるための 3 桁だけが残っています
  • ⇒ 少なくとも 1 つのセルには 有効な値がありません (矛盾)

したがって、赤い候補 d は除外できます。

---

2. ウォークスルー

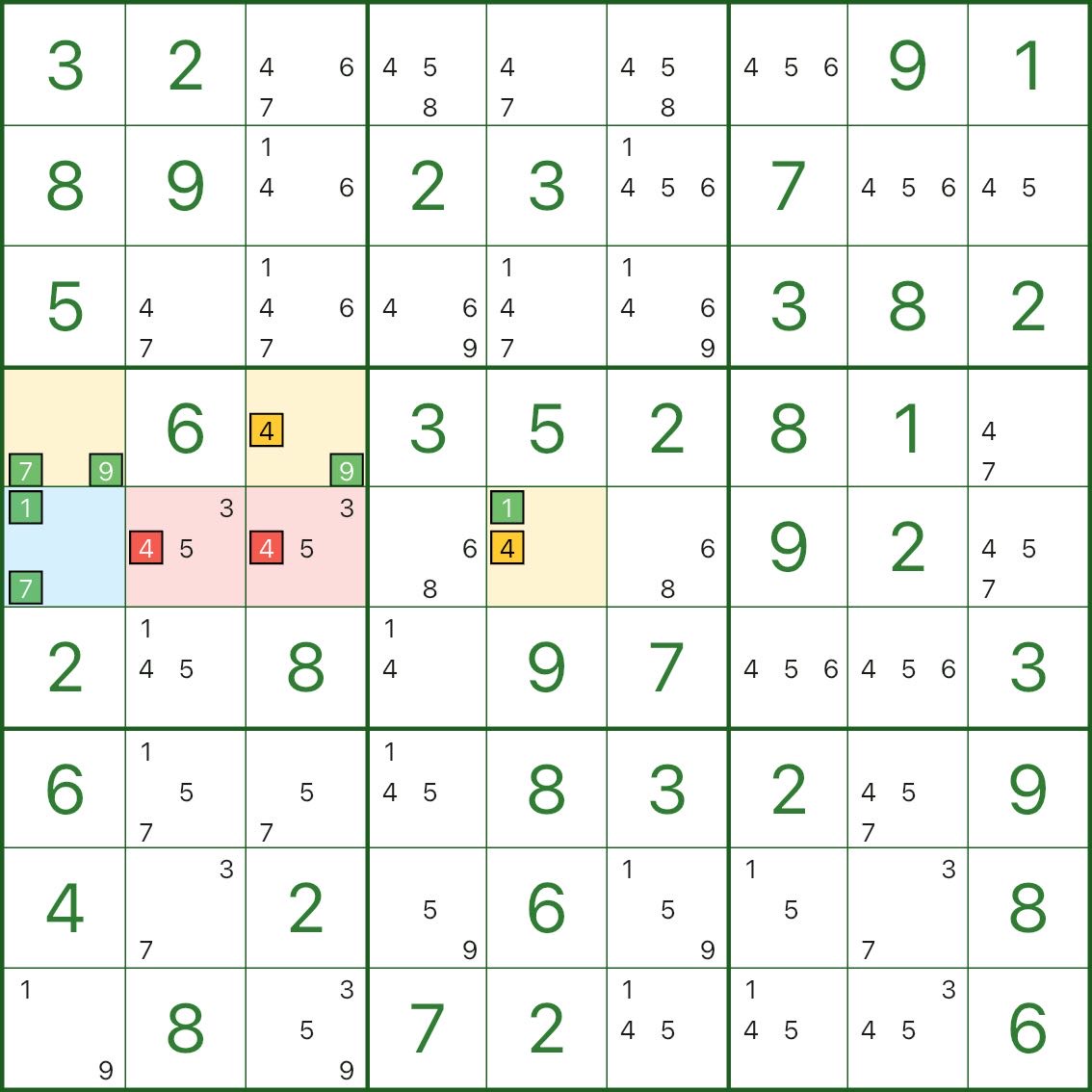
画像では、青がハブセル、黄色が翼、赤がエリミネーションです。
2 つの赤いセル (r4c2 と r4c3) の候補 4 を削除します。

赤い 4 はなぜ削除できるのですか?短い矛盾で十分です。

• 赤色の候補 4 が真であると仮定します
• その後、黄色の翼にある競合する 4 を削除する必要があります
• 翼は 1、7、9 の間でのみ強制的に分配されます (これらの数字は画像内ですでに強調表示されています)
• ただし、青いハブ セルにも 1、7 しか使用できません
  ウィングがハブに対して 1、7、9 を「使い切る/ブロック」すると、ハブ セルには 有効な値 が残ります (矛盾)

したがって、赤色の候補 4 は排除できるという仮定は不可能です。

---

3. 例

さらに 2 つの WXYZ-Wing の例を示します。青いハブ / 黄色のウィング / 赤いエリミネーションの構造を簡単に比較できます。

---

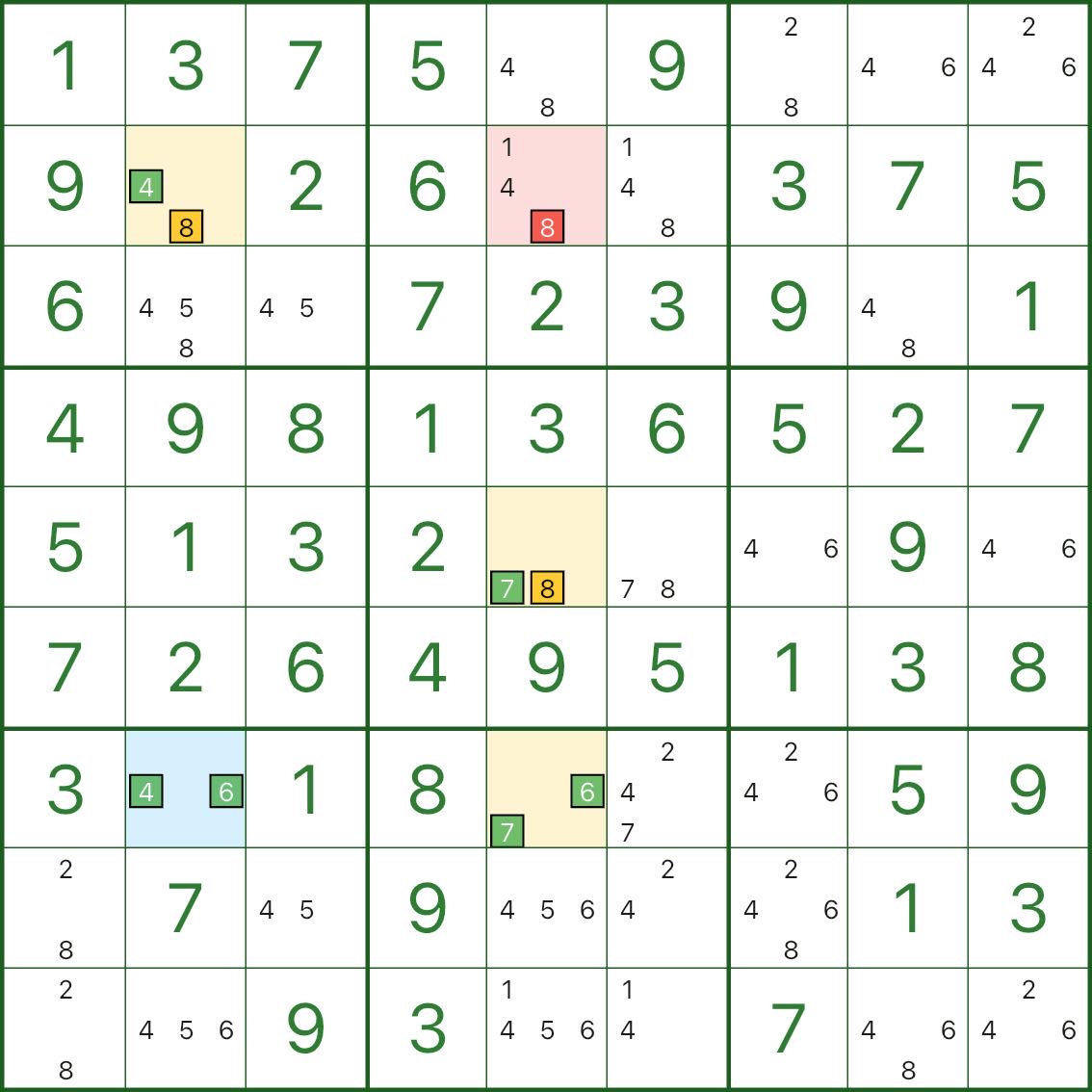
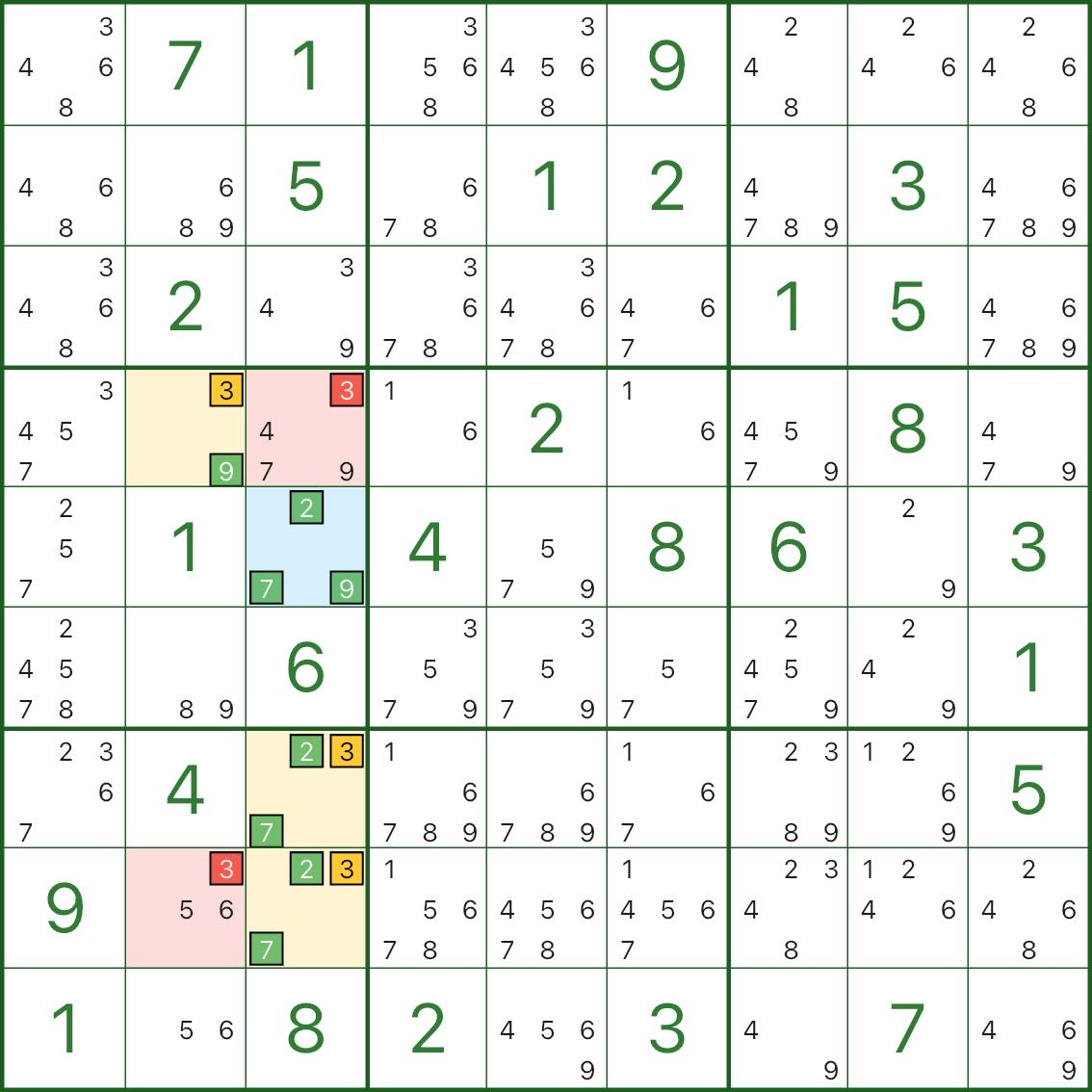
4. WXYZ-Wing の見分け方

一文でまとめると: 4 桁に制限された青/黄のクラスターを見つけて、簡単な矛盾を使って赤の候補をテストします。クラスターに値のないセルが残る場合は、それを削除できます。

実際には:

1. 細胞が局所的に相互に認識できる小さな色のクラスター (青 + 黄色) を探します。
2. そのクラスタ内のすべての候補が 4 桁に制限されているかどうかを確認します
3. 赤色の候補を見てください。これが正しいと仮定すると、数字が「押し出され」、色付きのセルに値がなくなる場合、消去法が得られます。
4. それを排除する