独自のソリューション

1. 競合なし ≠ 正しい

多くの初心者は次のように考えます。

「この数字は行、列、ボックスに表示されないので、配置できます。」

それは合理的に聞こえますが、多くの場合、間違っています。

＃＃＃ なぜ？ なぜなら、数独は「現時点で合法な数字を選ぶ」わけではないからです。
これは、完全な解決策が 1 つあるように設計された論理パズルです。

したがって、配置する数字は次のようになります。

• すぐには競合しない可能性があります
• ただし、将来の行/列/ボックスを行き止まりに強制する可能性はあります

そのため、このアプリでは次のことが表示される場合があります。
目に見える競合はまだありませんが、この動きはまだ間違っているとマークされています。

それは取締役会が 現在 対立しているからではなく、次の理由によるものです。
その値はパズルの一意の解決策に属すことはできません。

---

2. 例: 合法に見えますが、行き止まりにつながります

画像を使用して小さな例を見てみましょう。

ステップ 1: r6c6 は 1 である可能性があるようです

強調表示されたセル r6c6 を見てください。その行、列、ボックスには 1 はありません。
そこで次のように考えるかもしれません: ここに 1 を入れましょう

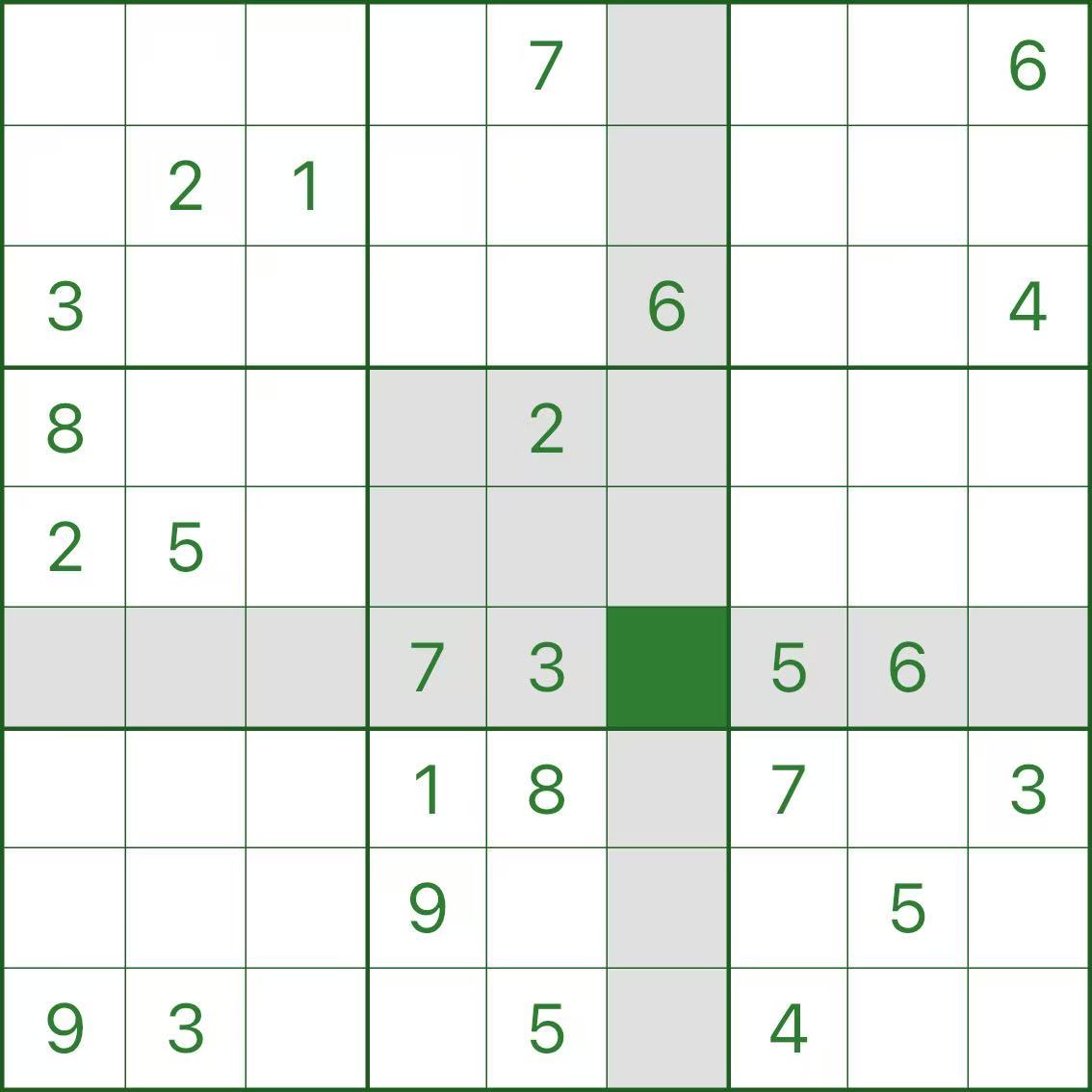
ステップ 2: r6c1 は強制的に 4 になります

次に、強調表示されたセル r6c1 を確認します。
行、列、ボックスにすでに表示されている数字を取り消し線で消すと、選択肢は 1 つだけ残ります: 4。

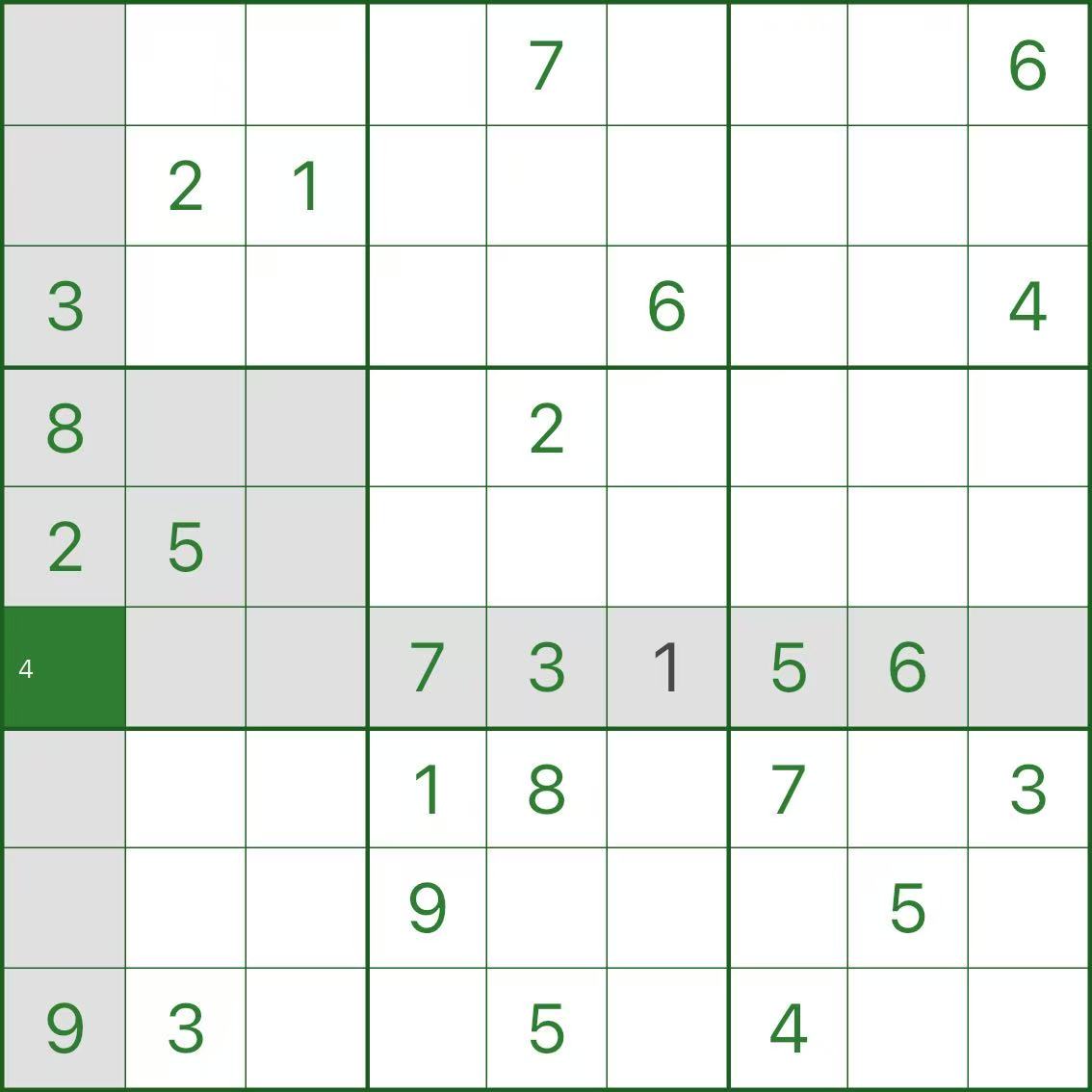
ステップ 3: r6c2 は強制的に 9 になります

次に、r6c2 を見てください。同じ消去を行うと、選択肢が 1 つだけ残ることがわかります (9)。

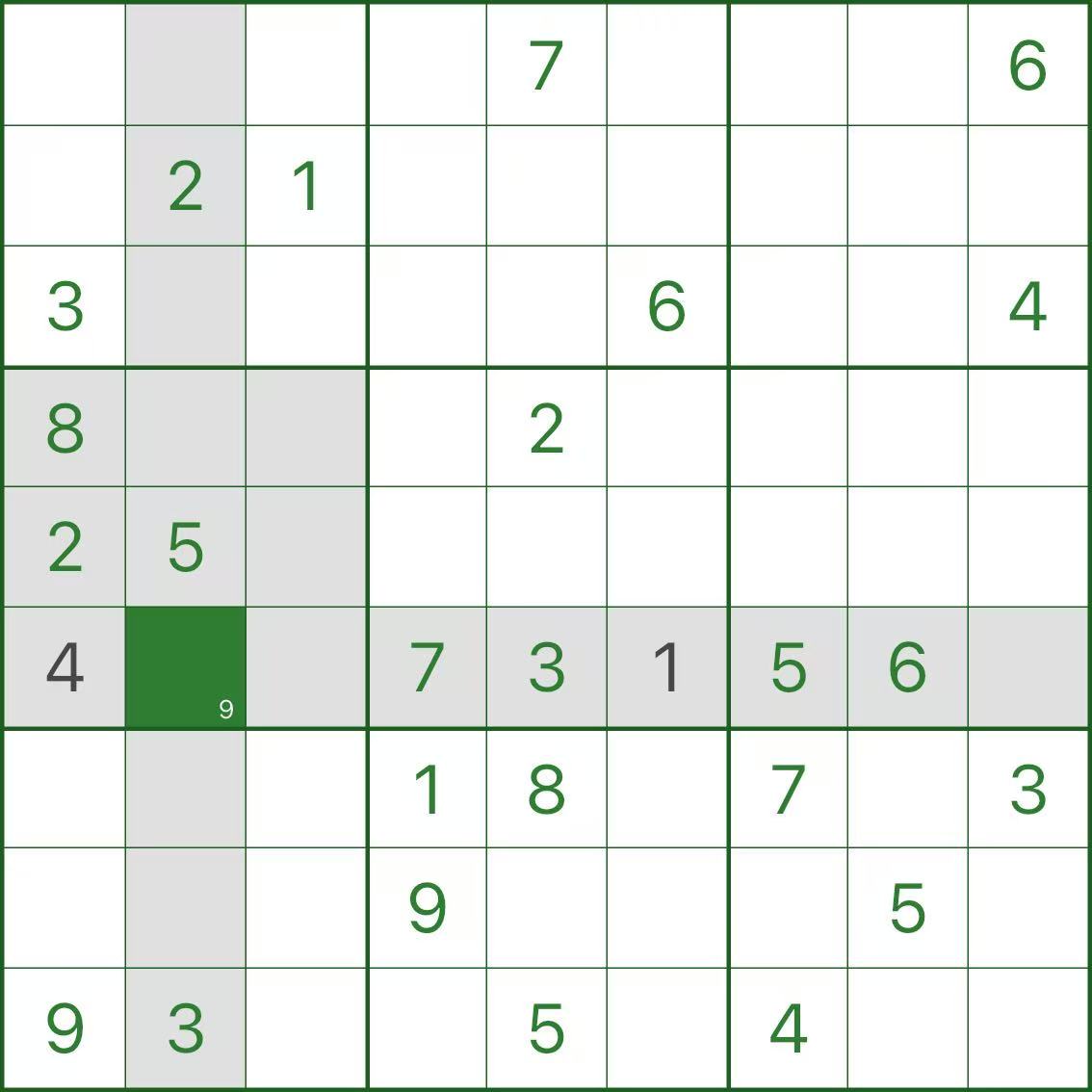
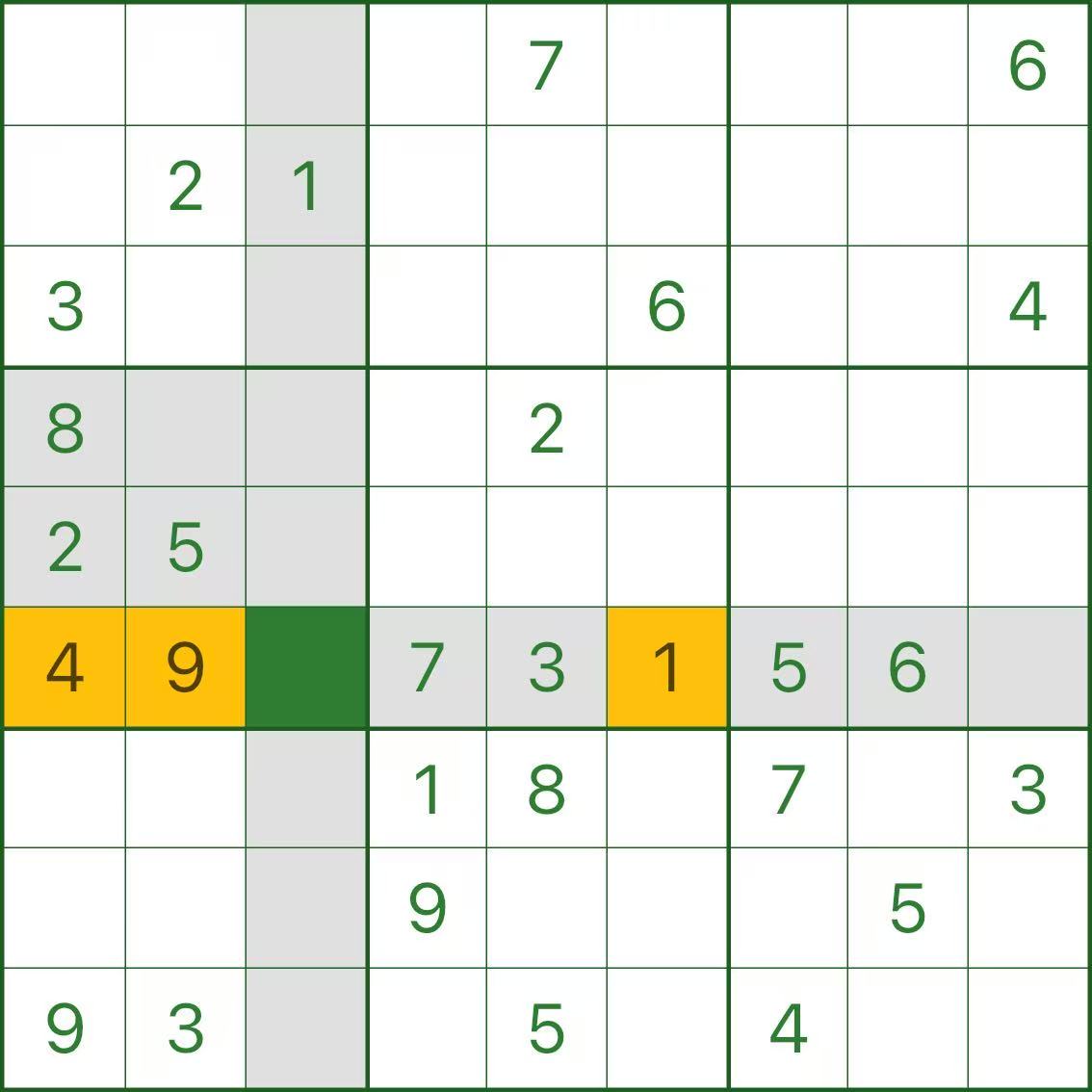
ステップ 4: r6c3 には可能な数値がありません。

これで r6c3 に到達しました。次のことがわかります。
1 から 9 までのすべての数字は行/列/ボックスによってブロックされているため、そこには何も配置できません。

言い換えれば、最初の「競合のない」手によって、最終的にパズルは行き止まりに追い込まれてしまいました。

参考: 正しい解決策

このパズルの正しい解決策を次に示しますので、比較してください。

---

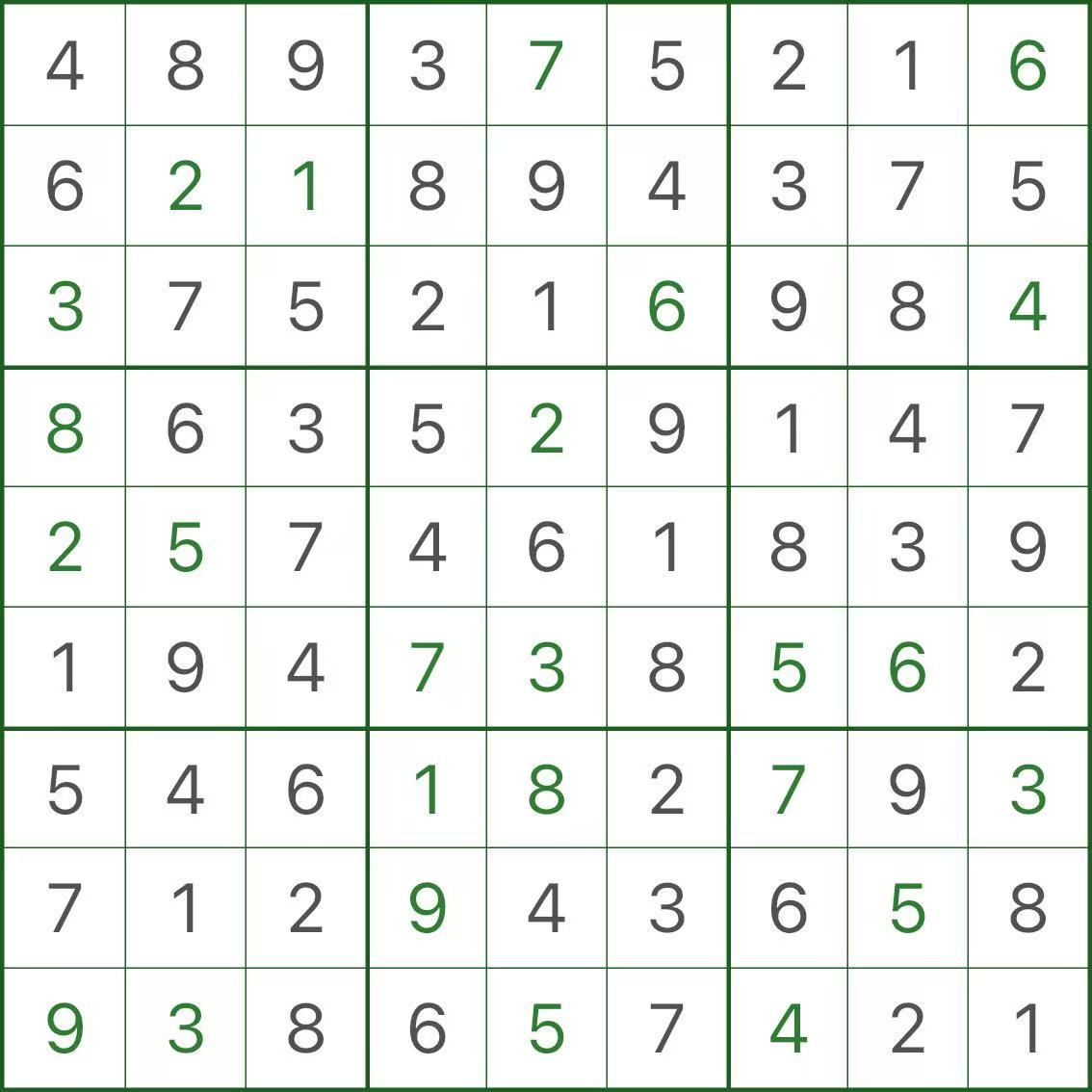
3. 正しい考え方: 「できる」だけではなく「しなければならない」ことを証明する

数独で最も重要な習慣は次のとおりです。

そこに行けるという理由だけで番号を入力しないでください。
そこに必ず行かなければならないことが証明できる場合にのみ配置してください。

よくわからない場合は、代わりに次のようにしてください。

• 鉛筆マーク (候補) を書き留めます。
• 消去法やその他の手法を使用して段階的に候補を絞ります
• セルに 候補が 1 つだけ残る、または数字が行/列/ボックス内に 1 つの場所だけになるまで

これにより、すべての動きが説明可能になり、ヒントが有効である理由がより明確になります。