ユニークな長方形 (UR)

前提条件: UR は、パズルには 正確に 1 つの解決策があるという事実に依存しています。
まだ読んでいない場合は、ここから始めてください。
Uniqueness

---

1. 概要

Unique Rectangle (UR) は、単一解 プロパティを使用して候補を排除する (場合によっては数値を配置する) テクニックのファミリーです。

「危険な形」に焦点を当てています。

• 4 つのセルが 2×2 の長方形を形成します (2 行×2 列、ちょうど 2 つのボックスにまたがります)。
• 4 隅すべてに同じ 2 つのコア候補が含まれています (たとえば、1 と 7)。

これら 4 つのセルにそのペアのみを残した場合、2 つの異なる方法 (2 つの数字を交換する) で四角形を塗りつぶすことができ、一意性が失われます。
したがって、一意性の仮定の下では、いくつかの候補を削除する必要があるか、セルが特定の値を取る必要があると結論付けることができます。

---

2. ウォークスルー（5種類）

以下の 5 つの画像は、5 つの一般的な UR タイプに対応しています (アプリ内のヒントではタイプ I ～ V としてラベル付けされています)。

カラーガイド:

• 青いセル: UR 長方形 (コア構造)
• 黄色のマーク: 推論で注目している候補
• 赤字：除外候補/または設定可能なセル

タイプ I: 単一屋根 → 強制値

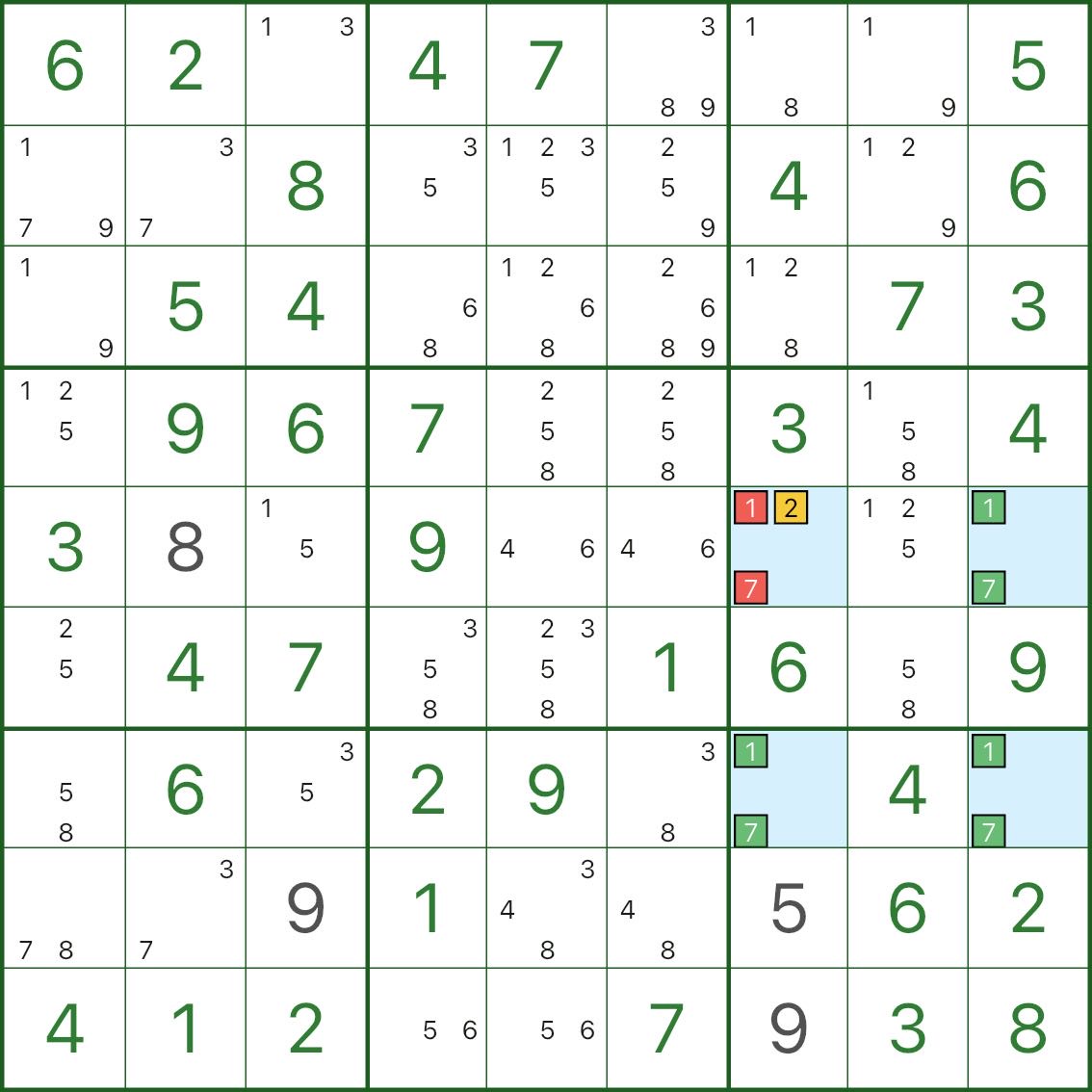
4 つの青いセルに注目してください。これらは長方形を形成しており、すべてに候補 1 と 7 が含まれています。
セル r5c7 には追加の候補 2 もあります。

r5c7 の 2 が 真 でない場合、r5c7 には 1 と 7 だけが残ります。
これにより、4 つの隅すべてが「{1,7} のみ」になり、2 つの交換可能な塗りつぶしが可能になります (一意性が失われます)。

したがって、一意性の下では次のようになります。

• r5c7 は候補 1 と 7 を保持できません
• したがって、r5c7 は 2 でなければなりません

---

タイプ II: 2 つの屋根 → 両方の屋根が表示される c を削除します

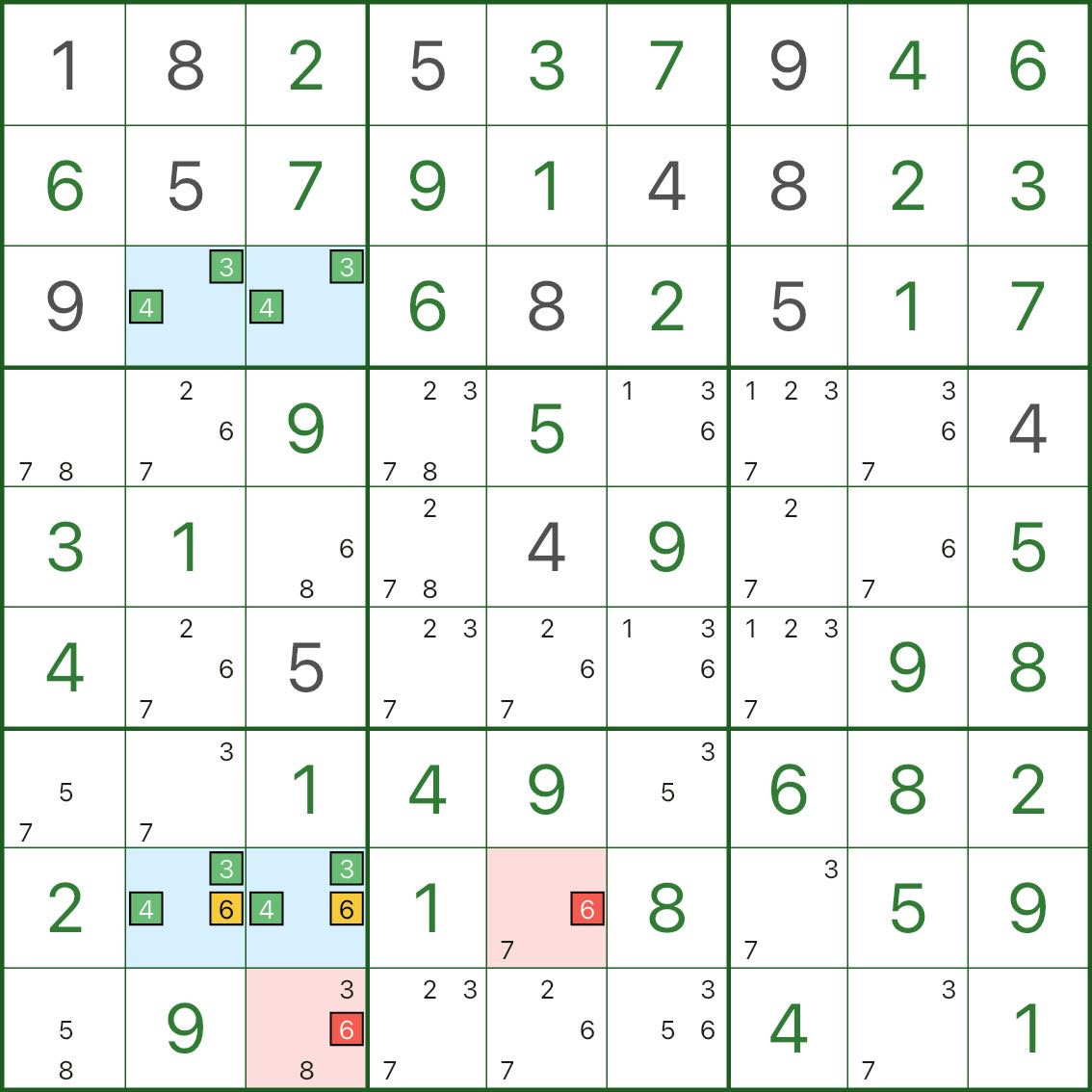
ここで、青い四角形はコア候補 3 と 4 に基づいています。
2 つの青いセル r8c2 と r8c3 にも候補 6 が含まれています (つまり、{3,4,6})。

ここで、両方の屋根セルが見える赤い候補 6 (r8c5 または r9c3 など) を考えてみましょう。

• 赤の 6 が本当であれば、両方の屋根は 6 ではなく になります。
• 屋根は {3,4} にのみ崩壊します。
• 長方形は再び致命的な {3,4} パターンになります (一意性が破壊されます)

したがって、これらの赤い 6 の候補は真実ではなく、除外される可能性があります。

---

タイプ III: 屋根を「パッケージ」として扱い、サブセットを形成します

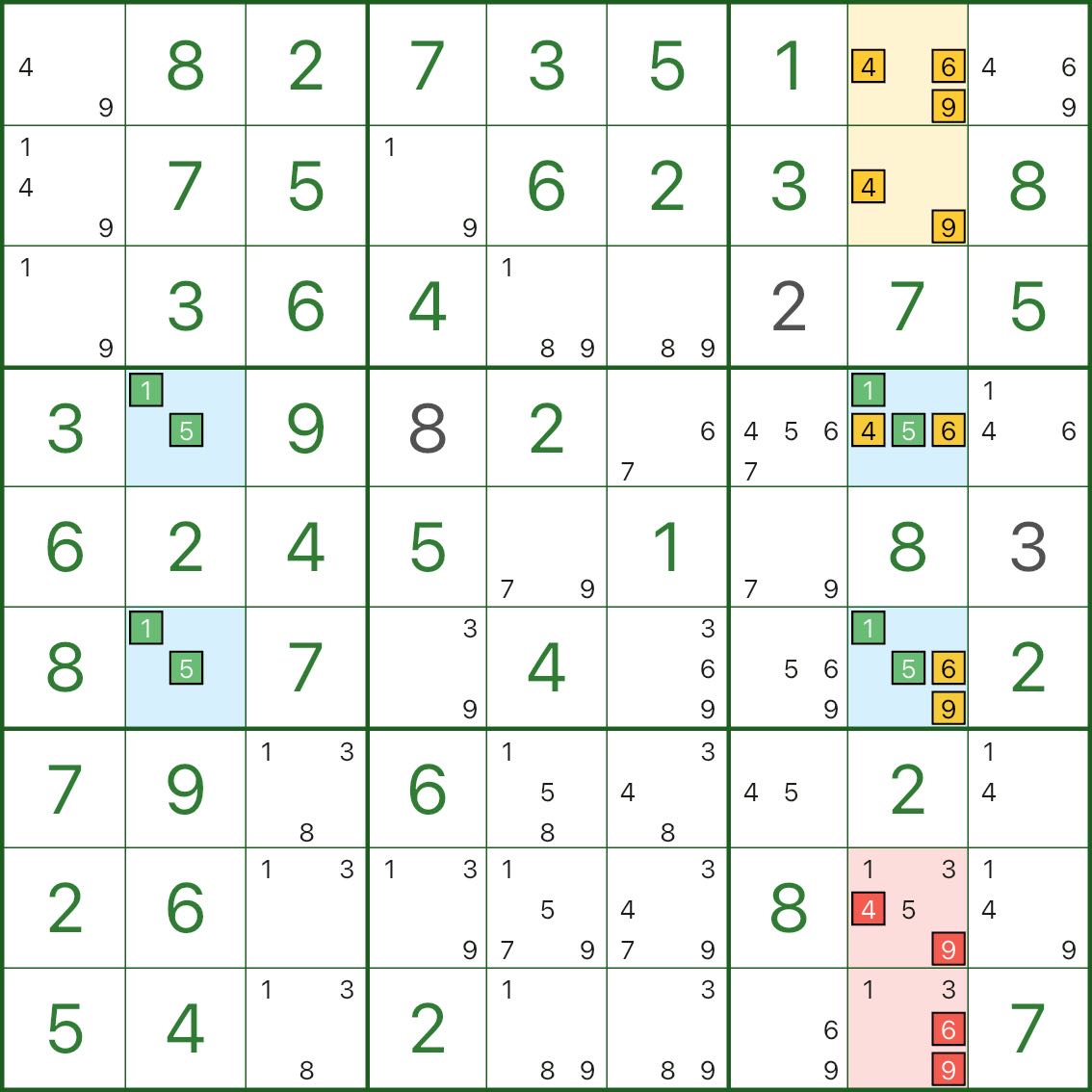
これは 列 8 に焦点を当てています。

• 列 8 の 2 つの青いセルには両方ともコア候補 1 と 5 が含まれています
• 追加の数字 4、6、9 も共有します (つまり、それぞれは {1,5,4,6,9})

一意性により、重要な制約が課せられます。

• これら 2 つの青いセルのうち、少なくとも 1 は {4,6,9} の数字を取る必要があります
• そうしないと、両方とも {1,5} のみに依存し、長方形が致命的なパターンに変わってしまいます。

したがって、「2 つの青いセルの余分な数字 {4,6,9}」をパッケージとして扱うことができます。
黄色のセル r1c8 および r2c8 と合わせて、これにより列 8 の小さなサブセット内の数字 4、6、9 が効果的にロックされます。

したがって、列 8 の他の 4/6/9 候補 (赤でマーク) は除外できます。

---

タイプ IV: 共役ペアにより 1 つの数字が強制され、もう 1 つの数字が削除されます。

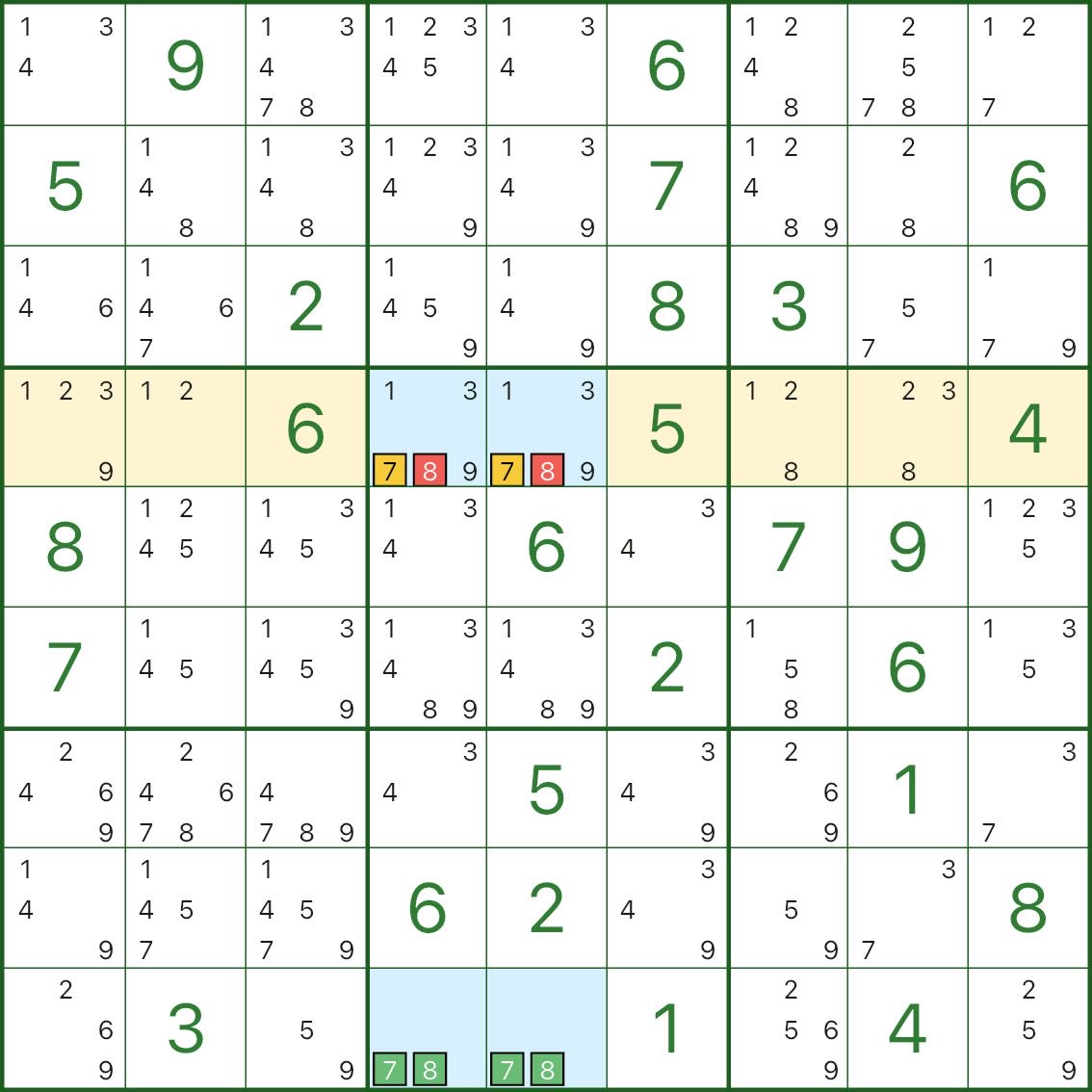
青い四角形は再びコア ペア (ここでは 7 と 8) に基づいて構築されます。行 4 では、候補 7 は 2 つの青いセル r4c4 と r4c5 にのみ表示されます。
つまり:

• r4c4 / r4c5 のいずれか 1 つは 7 でなければなりません

この制約がある場合、候補 8 を同じ青色のセル内に保持しても、長方形が致命的な構造に崩壊する (一意性が損なわれる) 可能性があります。

したがって、r4c4 と r4c5 から 8 を削除できます。

---

タイプ V: 複数の屋根 (2 または 3) → すべての屋根セルを表示する c を削除します。

タイプ V は厳密には「3 つの屋根」ではありません。重要なアイデアは次のとおりです。

• 長方形内には 2 または 3 の屋根セルがあり、それらはすべて同じ追加候補 c を共有します。
• 屋根セルが 2 のみの場合、通常、同じ行/列/ボックスを共有しません (共有する場合は、タイプ II に近くなります)
• セルの候補 c が屋根セルの すべて を見ることができる場合、その c は真ではなく、除外できます。

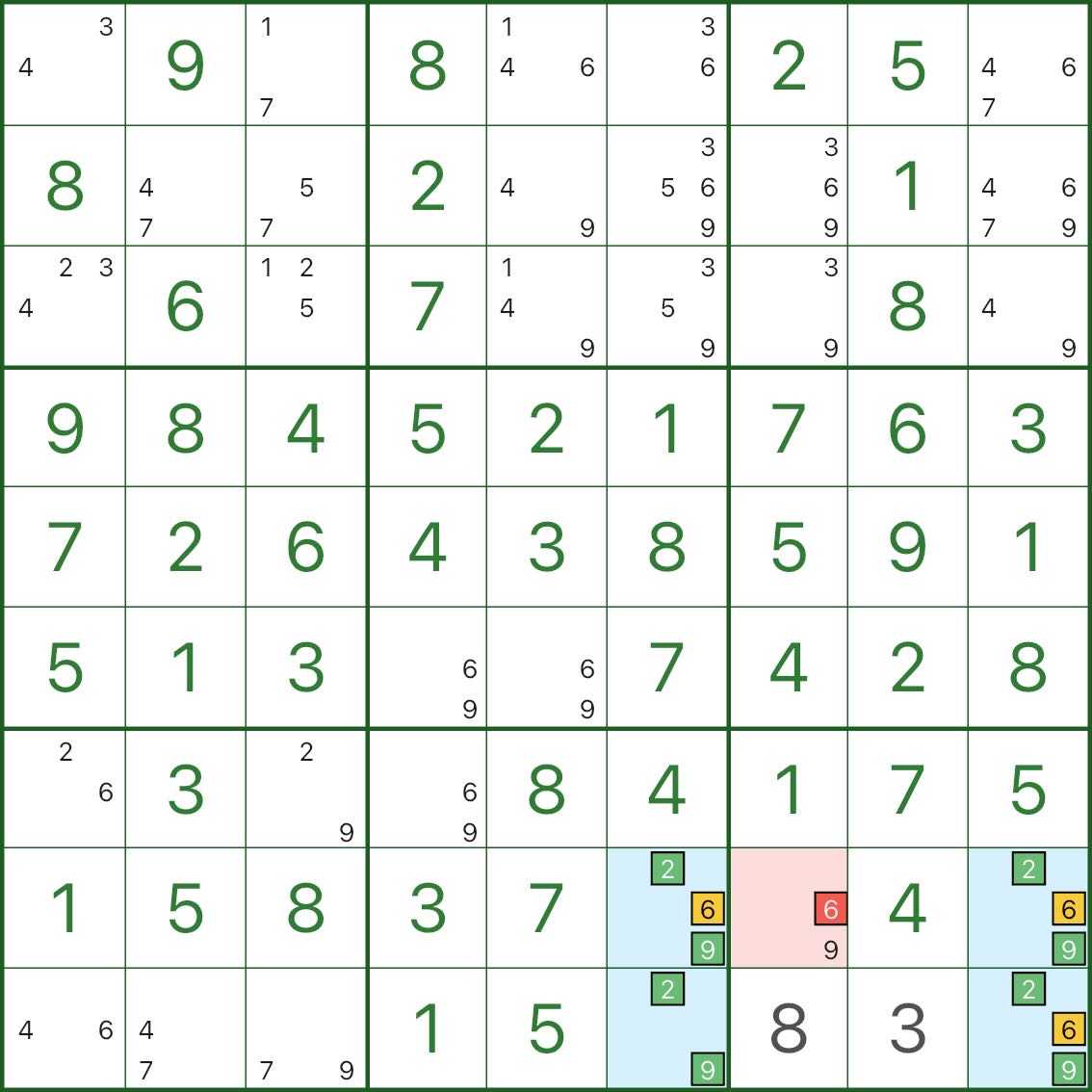
この画像では、青い四角形には主に数字 2、6、9 が含まれています。

• 3 つの青い角は {2,6,9}
• 残りの青いコーナーは {2,9} (6 がありません)

ここで、赤いセル r8c7 を見てください。これには候補 6 があり、このパターンの {2,6,9} ルーフ セルを すべて見ることができます。

r8c7 = 6 の場合:

• 3 つの屋根セルすべてが強制的に非 6 になります。
• それらは {2,9} のみに折りたたまれます
• 長方形は致命的な {2,9} パターンになります (一意性が破壊されます)

したがって、r8c7の候補6 は真であるはずがないため、除外できます。

---

3. 例

この記事の画像 1 ～ 5 は、すでにタイプ I ～ V の例です。
練習するときは、まず青い四角形を見つけてから、黄色/赤色のマークを上記の推論と一致させるようにしてください。

---

4. 固有の長方形を見つける方法

実際のパズルでは、次の順序で検索できます。

1. 2×2 の長方形 (2 行× 2 列) を形成し、ちょうど 2 つのボックスにまたがる 4 つの空のセルを探します。
2. 4 つのコーナーすべてが同じ 2 つのコア候補 (「デッドリー ペア」) を共有しているかどうかを確認します。
3. 次に、追加の候補がどのように見えるかによって分類します。
   • 1 つのコーナーのみに余分な候補があります → タイプ I (多くの場合、強制値)
   • 2 つの角が同じ追加桁 c を共有 → タイプ II
   • 屋根の追加桁は行/列/ボックスのサブセットを形成できます → タイプ III
   • 住宅では、1 つのコア数字が 2 つの長方形セルにのみ表示されます → タイプ IV
   • 2 つまたは 3 つのコーナーが同じ追加桁 c を共有します (2 つの屋根の場合、通常は家を共有しません) → タイプ V

これは UR を一言で表したものです。長方形が致命的なパターンに崩れることを決して許可しないでください。そうしないと、一意性が壊れてしまいます。