解法ガイド / ペアとサブセット
ペアとサブセット
> 裸/隠されたペアとサブセット
初級
ペアとサブセット
裸/隠されたペアとサブセット
ペアとサブセットは、最も有用な「候補排除」テクニックの一部です。名前は異なりますが、実行することはすべて同じです。
1 つの ハウス (行/列/ボックス) では、セルの小さなセットと数字の小さなセットが相互に「スロットを予約」します。そのため、それらの数字はそのハウスの他の場所に表示されません。
専門用語を覚える必要はありません。簡単な経験則:
- 裸: セルに表示される内容から開始します (これらのセルにはこれらの数字のみが含まれます)
- 非表示: 数字を入力できる場所から開始します (これらの数字はこれらのセルにのみ入力できます)
1. 裸のペア
同じハウス内で、2 つのセルの両方に 同じ 2 つの候補のみ (例: {a,b}) が含まれている場合、ネイキッド ペアが存在します。
つまり:
- 1 つのセルは a でなければならず、もう 1 つのセルは b でなければなりません (順序は不明)
- したがって、候補 a と b は、そのハウス内の 1 つおきの空のセルから削除できます。
まず、下の画像を見てください。強調表示されたボックス 3 と 2 つの緑色のセル r2c9 と r3c9 に注目してください。
{1,5} のみであることがわかります。
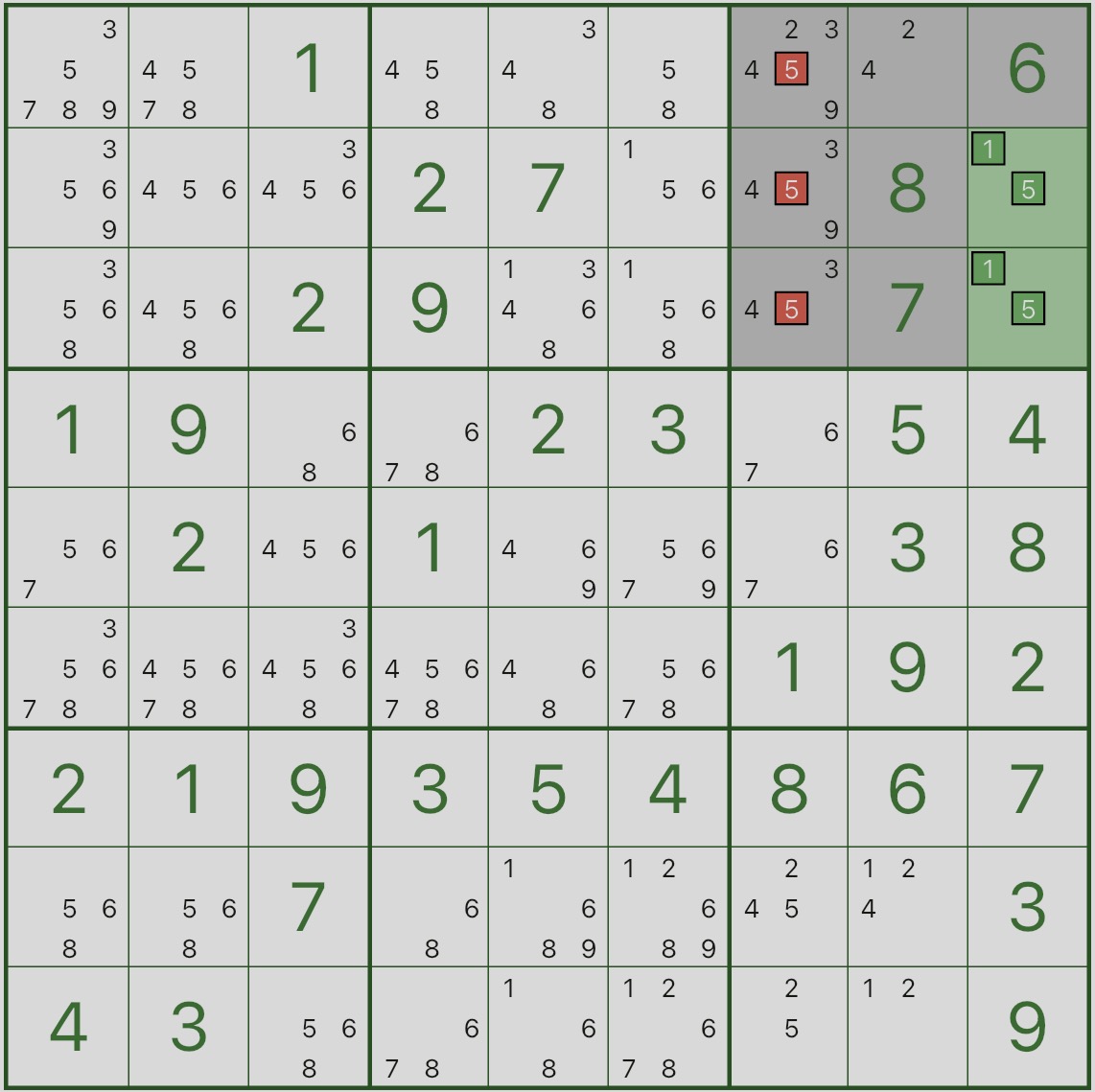
これは、ボックス 3 では、1 と 5 の数字がr2c9とr3c9用に「予約」 されていることを意味します。
次に、赤色の候補を見てください。r1c7、r2c7、r3c7 の候補 5 は削除できます。
矛盾による簡単な証明:
- r1c7 が 5 であると仮定します (同じロジックが r2c7 と r3c7 に適用されます)。
- この場合、ボックス 3 にはすでに 5 が含まれているため、r2c9 と r3c9 は 5 にはならず、強制的に 1 になります。
- ただし、r2c9 と r3c9 は同じ列 (列 9) を共有しているため、両方を 1 にすることはできません — 矛盾しています
⇒ 赤5候補は無理なので除外可能
2. 隠れたペア
同じハウス内で、候補 a がちょうど 2 つのセルに表示され、候補 b も 同じ 2 つのセルに表示される場合、隠れたペアが存在します。
これら 2 つのセルには追加の候補が表示される場合がありますが、a と b はすでにそれらにロックされているため、次のことが可能です。
- これら 2 つのセルから a と b を除くすべての候補を削除します
まず、下の画像を見てください。強調表示された列 4 に注目してください。
その列の候補 4 と 5 が表示される場所を見つけます。これらは r1c4 と r6c4 にのみ表示されることがわかります。
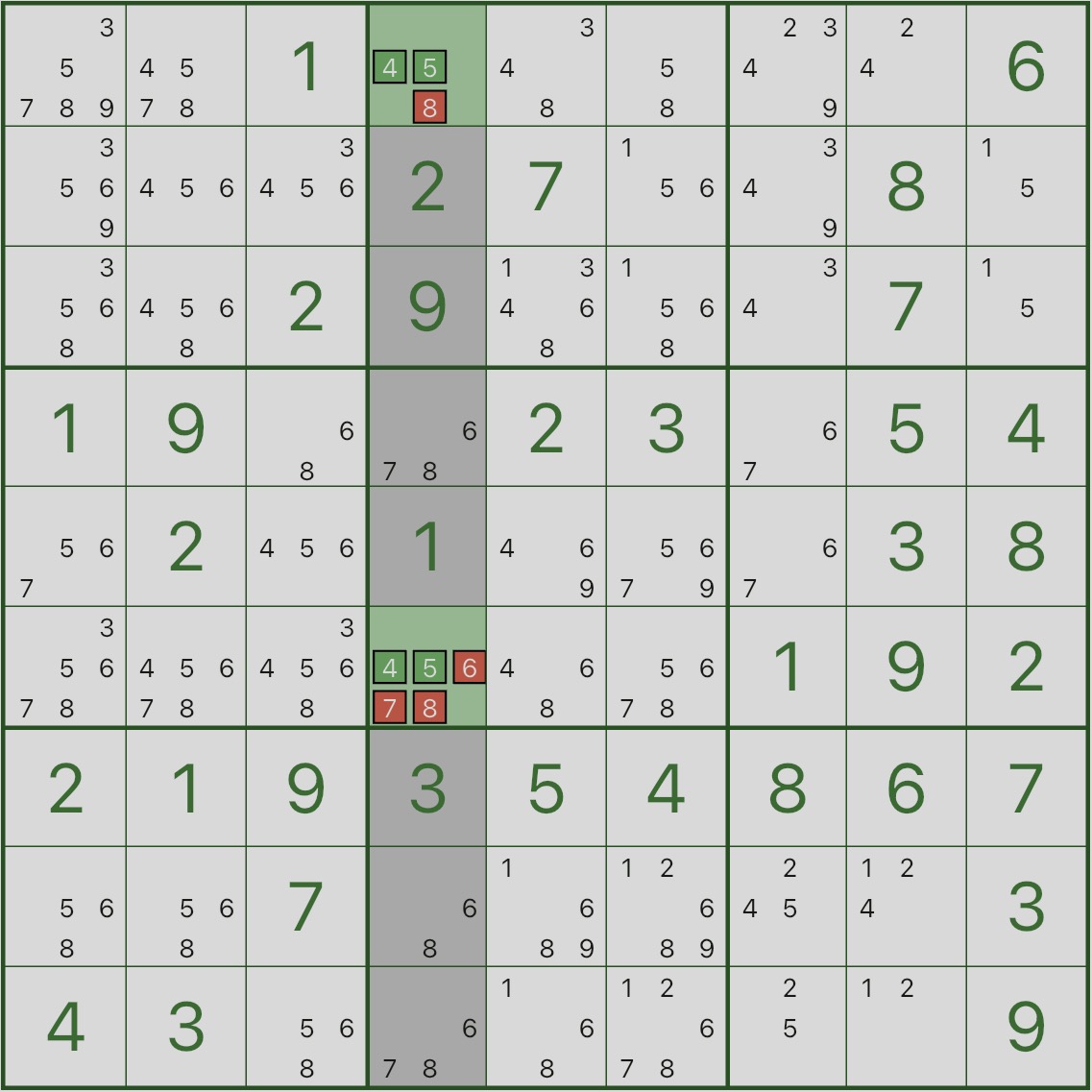
これは、列 4 の 4 および 5 を r1c4 および r6c4 に配置する必要があることを意味します。
r1c4 と r6c4 から他の候補を削除できるのはなぜですか?
- r1c4 が 4 または 5 以外の数字を取ると仮定します
- その場合、4 と 5 の両方が r6c4 のみ に適合する必要があります。
- 単一のセルが 4 と 5 の両方になることはできません — 矛盾
⇒ r1c4 と r6c4 は {4,5} である必要があるため、これらのセル内の他の候補は削除できます。
3. ネイキッドサブセット (トリプル/クアッド)
これは「裸のペア」のアイデアを一般化したものです。
家の N 個のセル に集合的に N 桁 だけが含まれる場合 (たとえば、3 つのセルに {a,b,c} のみが含まれる)、ネイキッド トリプルが存在します。同じ考え方がクワッドにも当てはまります。
これらの数字は N 個のセル内に配置する必要があるため、次のようになります。
- その家の 1 つおきの空のセルからそれらの数字 (a、b、c など) を削除します。
まず、下の画像を見てください。強調表示された行 8 と 3 つのセル r8c1、r8c2、r8c4 に注目してください。
これら 3 つのセルには、合計で {5,6,8} のみが含まれていることがわかります。
これは、行 8 では、数字 5、6、8 を r8c1、r8c2、r8c4 内に配置する必要があることを意味します。
そのため、8 行目の残りの赤い 5、6、8 の候補を削除できます。
単純な矛盾の見方:
- 行 8 の別のセルが {5,6,8} のいずれかを「取得」した場合
- その場合、これら 3 つのセルには 2 桁のみを使用して入力する必要があります。
- それはうまくいきません — 矛盾しています
4. 隠れたサブセット (トリプル/クアッド)
これは「隠れペア」のアイデアを一般化したものです。
ハウス内の N 桁が同じ N セル にのみ表示される場合 (セルに余分な候補が含まれている場合でも)、隠れたトリプル/クアッドが存在します。
これらの N 桁は N 個のセルにロックされているため、次のようになります。
- これらのセルから N 桁を除くすべての候補を削除します
まず、下の画像を見てください。強調表示された列 5 に注目してください。
数字 4、7、8 は r1c5、r8c5、r9c5 にのみ表示されることがわかります。
これは、列 5 では、数字 4、7、8 を r1c5、r8c5、r9c5 内に配置する必要があることを意味します。
したがって、これら 3 つのセルでは、4、7、または 8 以外の他の候補を削除できます。
なぜそれが安全なのでしょうか?
- これらのセルのいずれかが異なる桁を取得した場合
- その場合、4、7、8 には適合するスポットが 3 つ未満になります — 矛盾
5. より早く発見するためのヒント
- 候補を適度に完成させておきます (より難しいパズルには候補が必要になります)
- 最初にネイキッド パターンをスキャンします。候補が非常に少ない (2、3、または 4) セルから開始します。
- 次に、隠れたパターンをスキャンします。家の中で、数字が 2、3、または 4 つのスポットに制限されているかどうかを確認します。
- 除外後、一時停止してもう一度確認します。単純化された候補によって、次のステップが明らかになります。