空の長方形

前提条件: Chain Basics

説明

空の長方形は、1 桁の 候補排除テクニックです。1 桁の d に焦点を当てます。

ボックス内では、数字 d が特別な 十字/L 字型分布を形成する場合があります。つまり、そのボックス内のすべての d 個の候補が 1 行 1 列に存在することを意味します。
短いチェーンがこれらの行に d を強制すると、非常に明らかな矛盾に到達することがあります。ボックスには d を入れる場所がなくなってしまうため、元の仮定は間違っているに違いありません。

---

説明

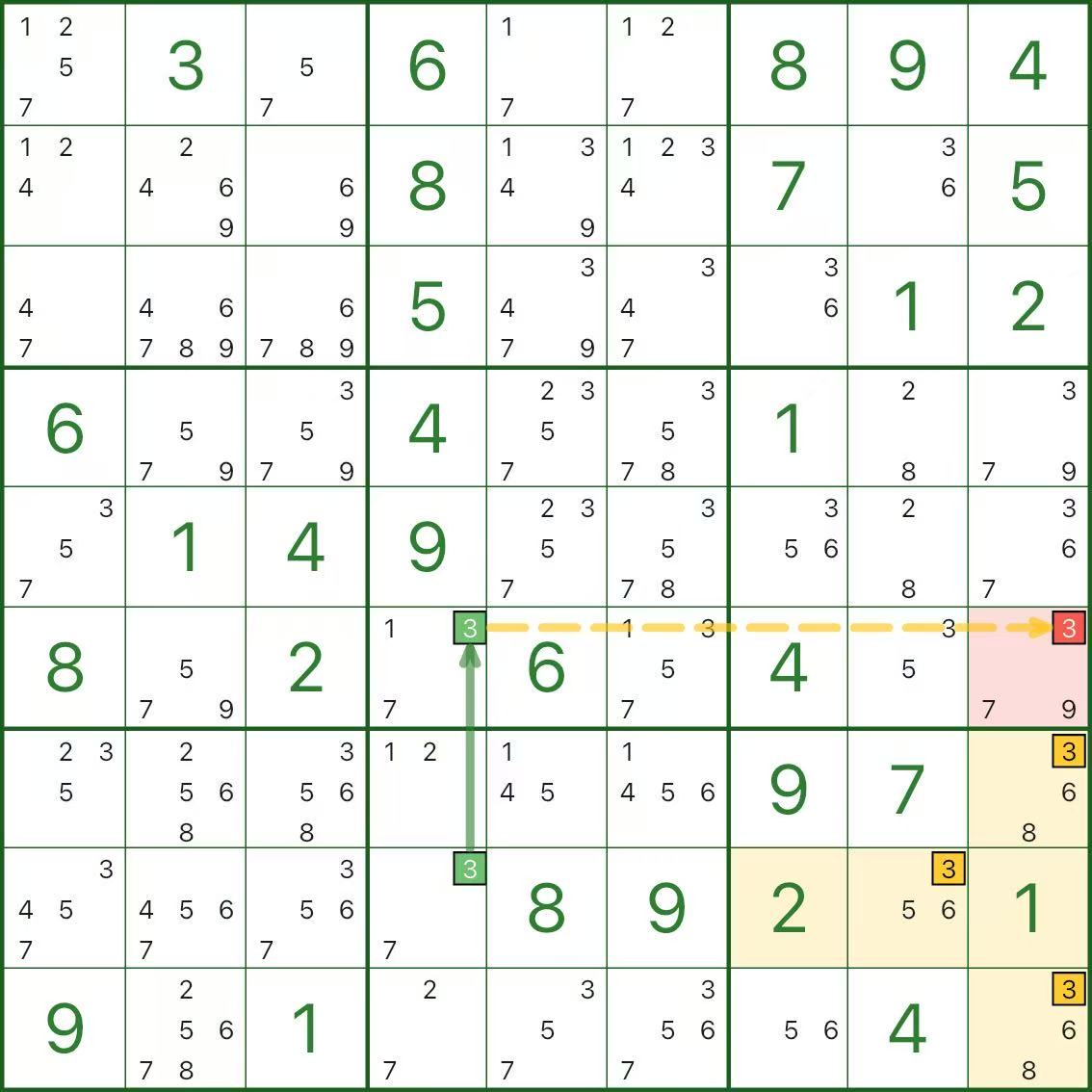
上の画像では、r6c9の候補 3 (赤) を削除したいと考えています。

短い矛盾は次のとおりです。

• r6c9 = 3 と仮定します (赤色の候補が 真)
• 行に 3 を 2 つ含めることはできないため、r6c4 ≠ 3
• 列 4 の数字 3 には、r6c4 または r8c4 の 2 つのセルしかありません。
  r6c4 は 3 ではないため、r8c4 は 3 でなければなりません
• ここでボックス 9 (空の長方形のボックス) を見てください。
  r6c9 = 3 (同じ列) および r8c4 = 3 (同じ行) では、ボックス 9 の残りの 3 つの位置がすべて削除されるため、ボックス 9 には数字 3 を入れる場所がありません (矛盾)

したがって、次の仮定は不可能です。r6c9 は 3 であることはできず、候補 3 は除外できます。

---

例

これらの画像には、より多くの空の長方形パターンが示されています。 「ボックスクロス/L字+ショートチェーン+エリミネーション(赤)」の参考にしてください。

---

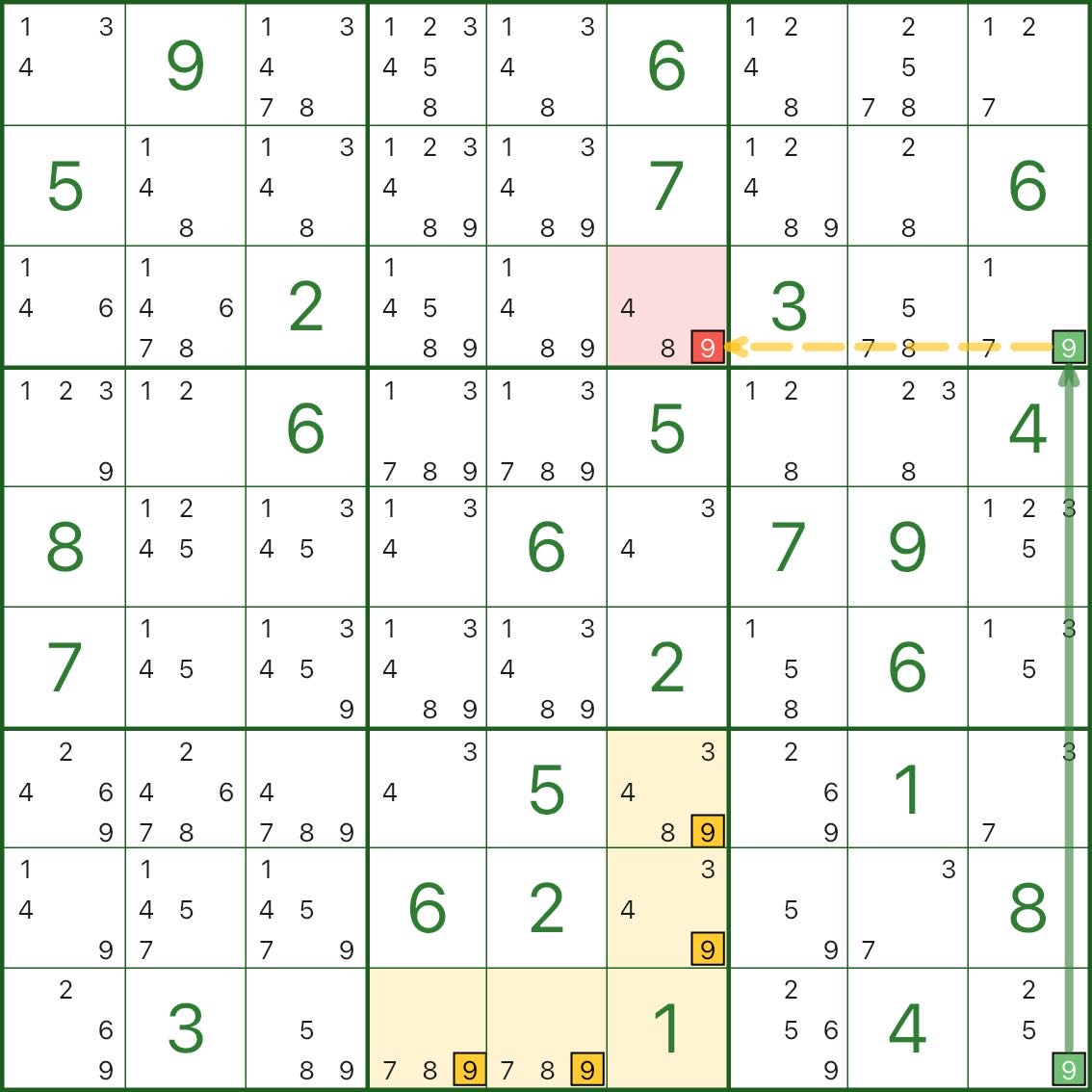
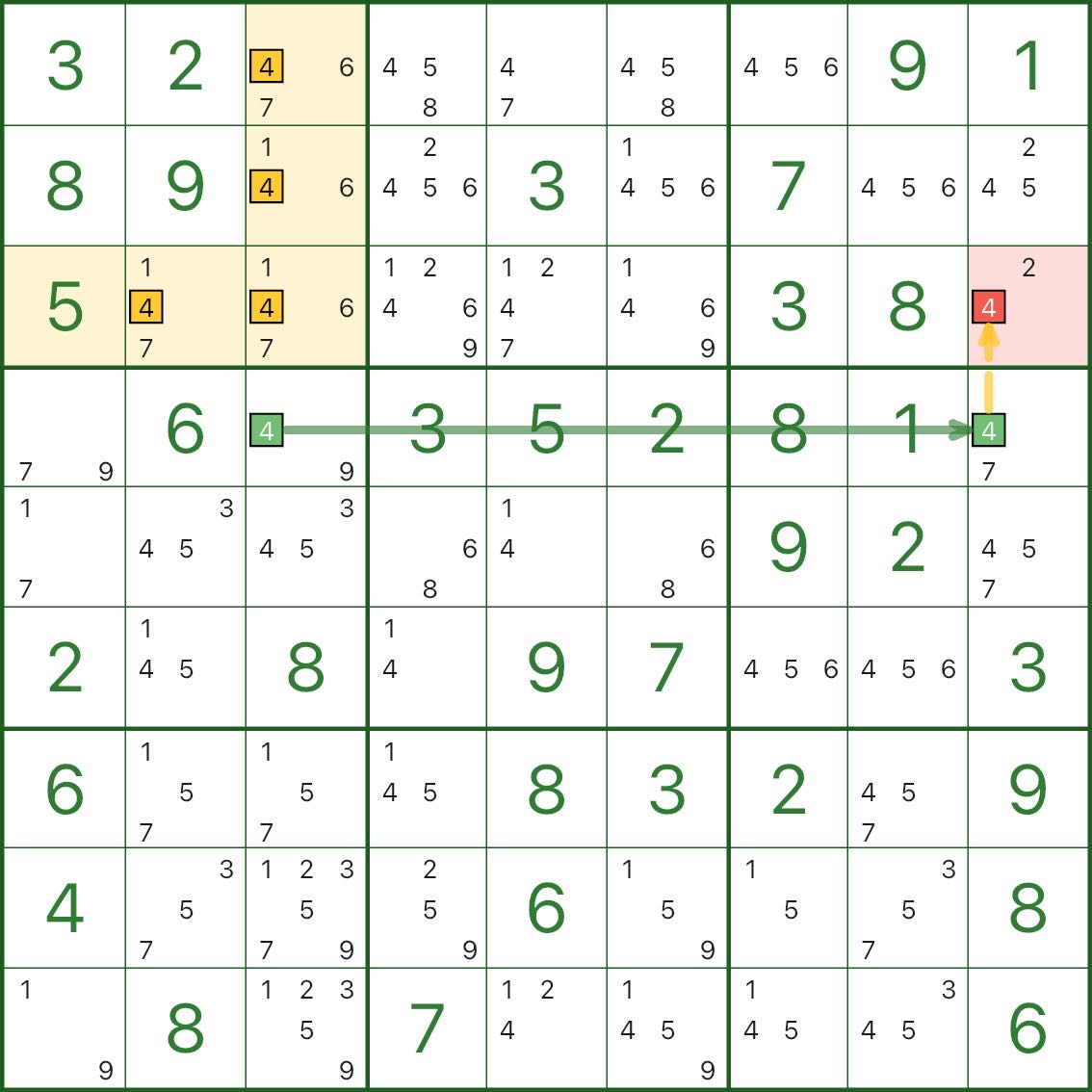
空の四角形を見つける方法

1 行のチェックリスト: d 個の候補が十字/L 字形を形成するボックスを見つけ、ボックスに d の場所がなくなるような短いチェーンを使用し、矛盾により赤い候補を削除します。

実際のパズルでは:

1. 数字 d を選択してください
2. ボックス内で、すべての d 候補が 1 行 + 1 列 (十字/L 字型) にあるかどうかを確認します。
3. 赤い候補が真であると仮定して d をそれらの行に強制するように、短いチェーンを探します。
4. この仮定により、ボックスに d が入る場所がない場合は、赤色の候補 d を削除します。