基本的なカラーリング

前提条件: Chain Basics

説明

基本的な色付けは、1 桁の 候補除外手法です。1 つの桁 d に焦点を当て、二重位置 (数字 d が 2 つの候補セルに現れる行/列/ボックス) からの強いリンクのみを使用します。

2 色 (青/黄色) を使用して、強いリンクに沿って候補を「色付け」します。
これら 2 つの色は、相互に排他的な 2 つの演繹ルートを表します。強いリンクでは、ちょうど一方の端が真であるため、色が交互になります。

1 つの色のチェーンでは、青と黄色を 2 つの反対の仮定として考えることができます。

• 青が真であると仮定します ⇒ 黄色は偽です
• 青は偽であると仮定します ⇒ 黄色は真です

したがって、同じ強いリンクでは、2 つの色のうち 1 つが真である必要があります。

基本的な色付けでは、通常、次の 2 種類の結論が得られます。

1. トラップ: 赤の候補には青の候補と黄色の候補が 1 人ずつ見える → 赤の候補は排除される可能性がある
2. 同色矛盾: 1 つの家に同じ色の 2 つの候補が出現 → その色全体を排除することは不可能である

---

トラップ

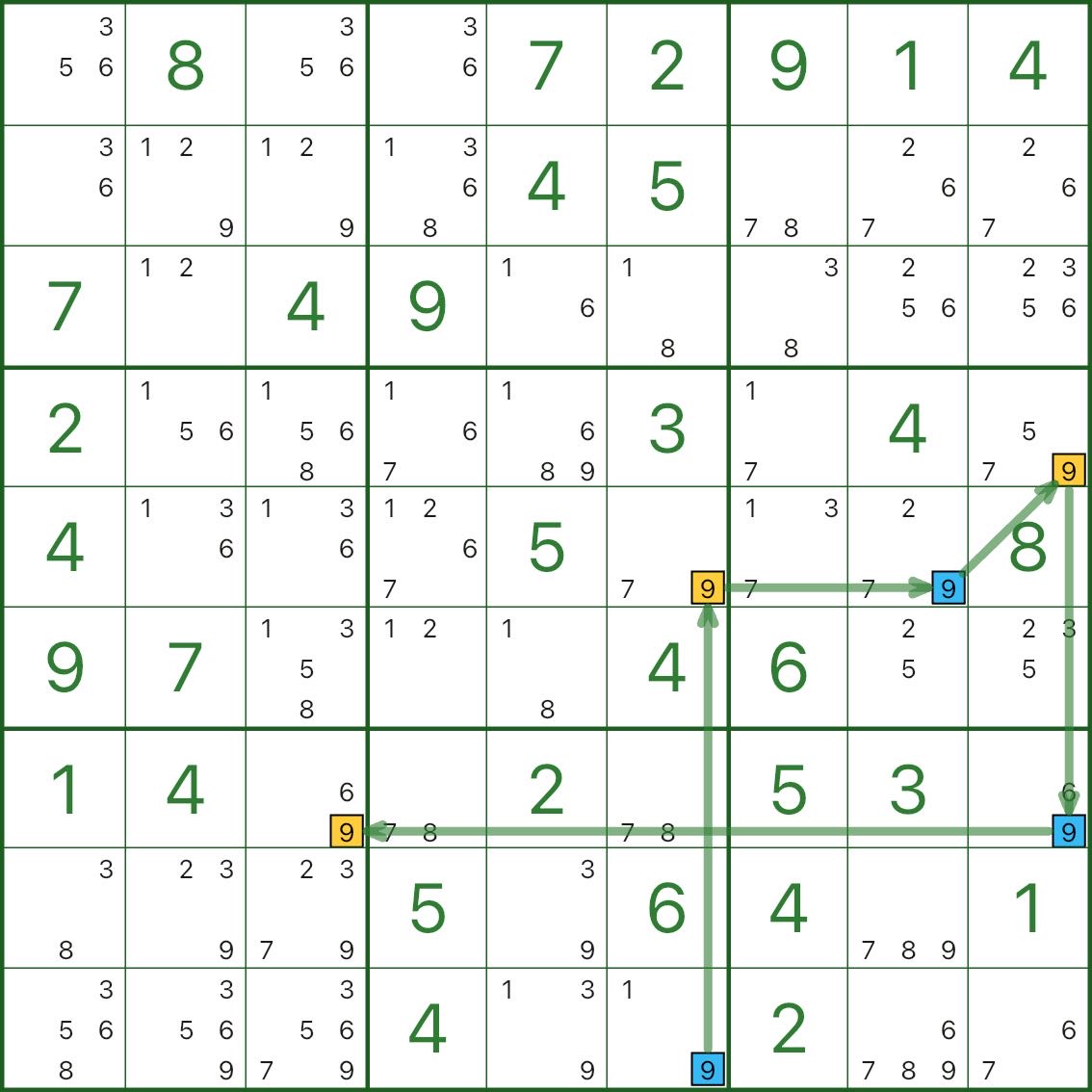
画像 1 では、ターゲットの桁は 9 です。 r9c6 から始まる強リンク鎖に色を付けます。もう 1 つのエンドポイントは r7c3 (青/黄) です。

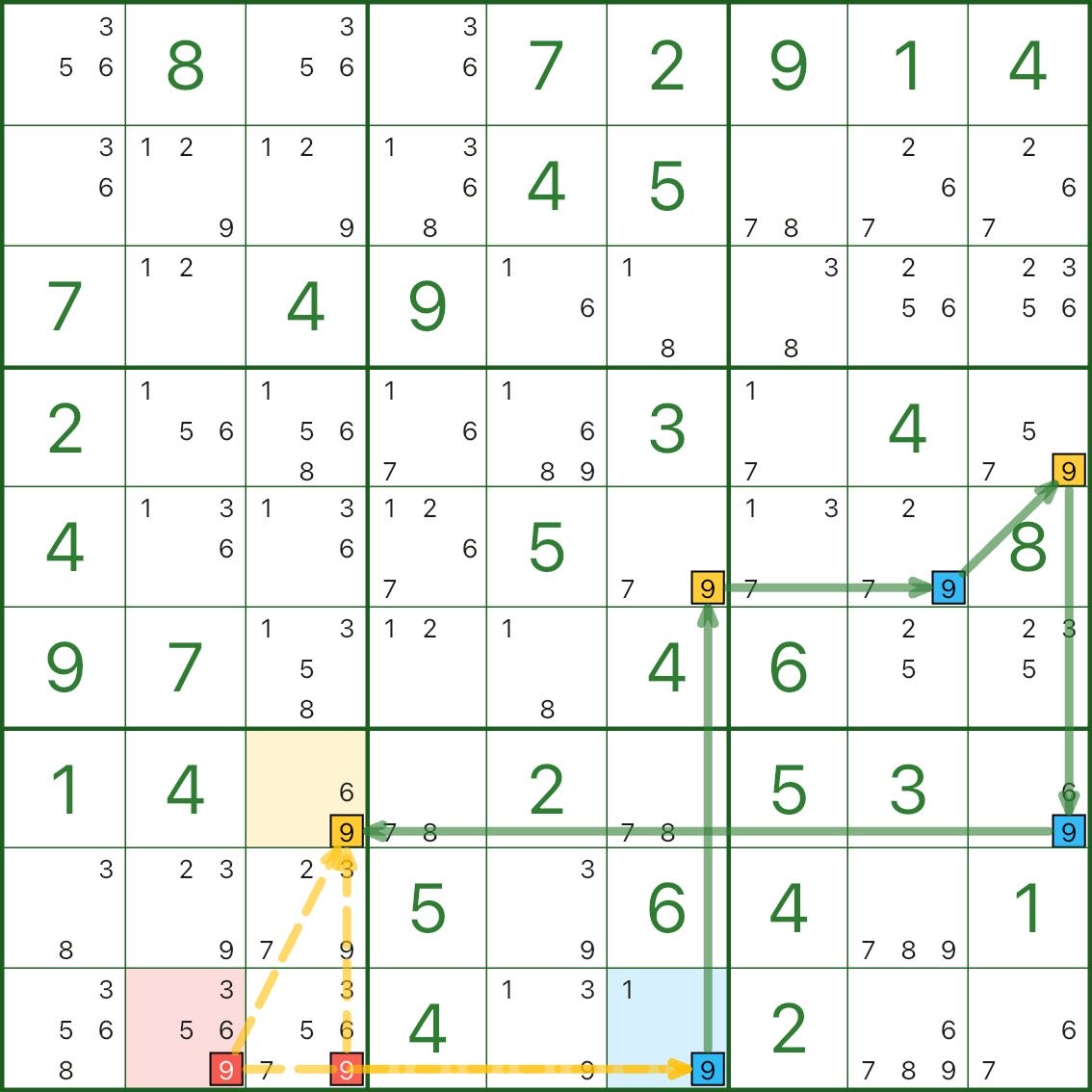
画像 2 では、赤色の候補は r9c2 の候補 9 と r9c3 の候補 9 です。
なぜ削除できるのでしょうか?重要なアイデアは次のとおりです。

• 青が 真 の場合、青のエンドポイント (r9c6 など) は 9 です。赤の候補にはそれが見えるため、青のエンドポイントと競合するため、9 にすることはできません。
• 青が 偽 の場合、同じ強いリンク上で黄色のエンドポイントが真である必要があります (たとえば、r7c3 は 9)。赤い候補にもそれが見えるので、依然として対立しており、9になることはできません。

いずれにせよ、赤い候補は9人になることはできないので、除外することができます。

---

同色の矛盾

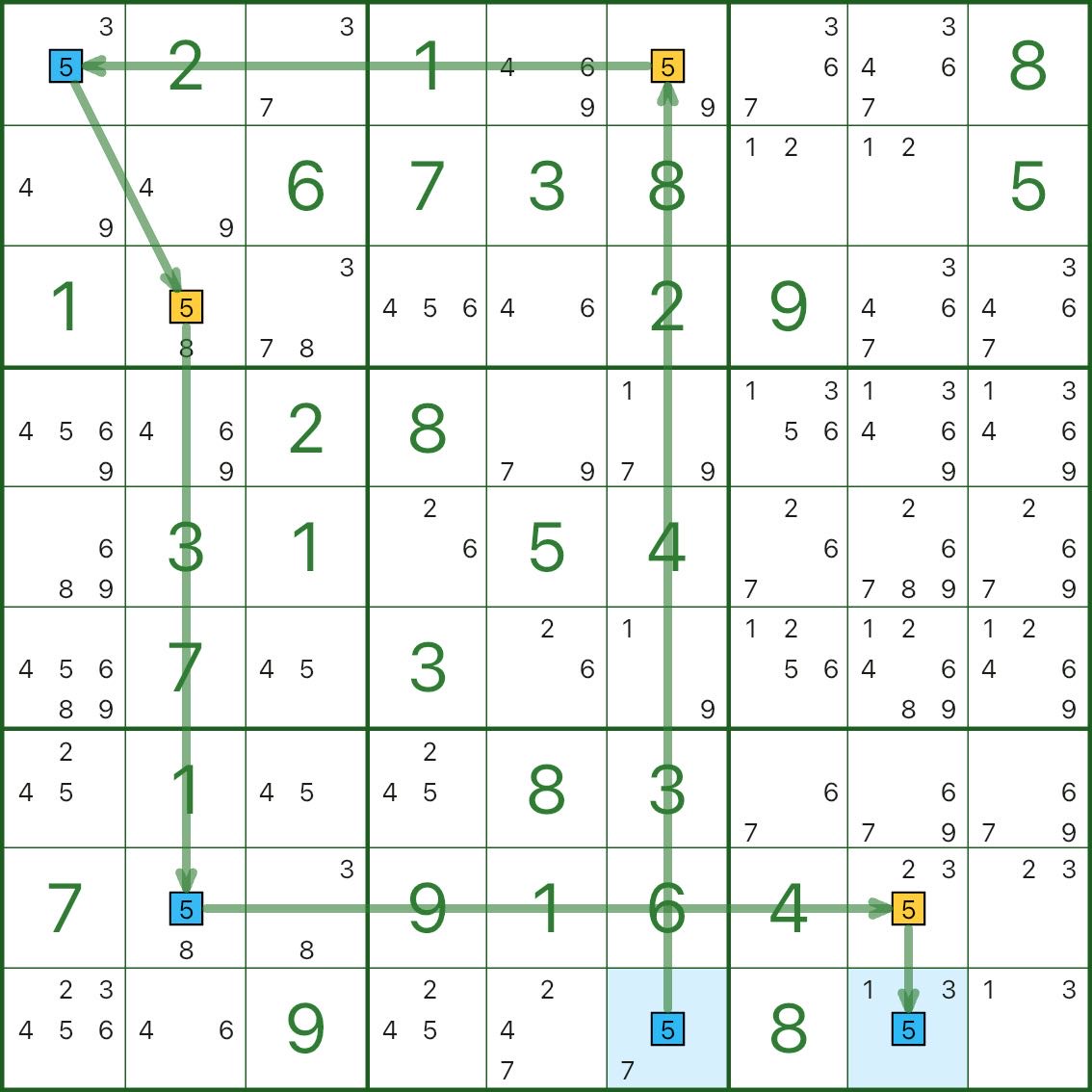
画像 3 では、ターゲットの桁は 5 です。 r9c6 から始まり、チェーンは最終的に r9c8 も青の 5 になります。
しかし、r9c6 と r9c8 は同じ行にあるため、両方とも 5 になることはできません。これは同じ色の矛盾です。

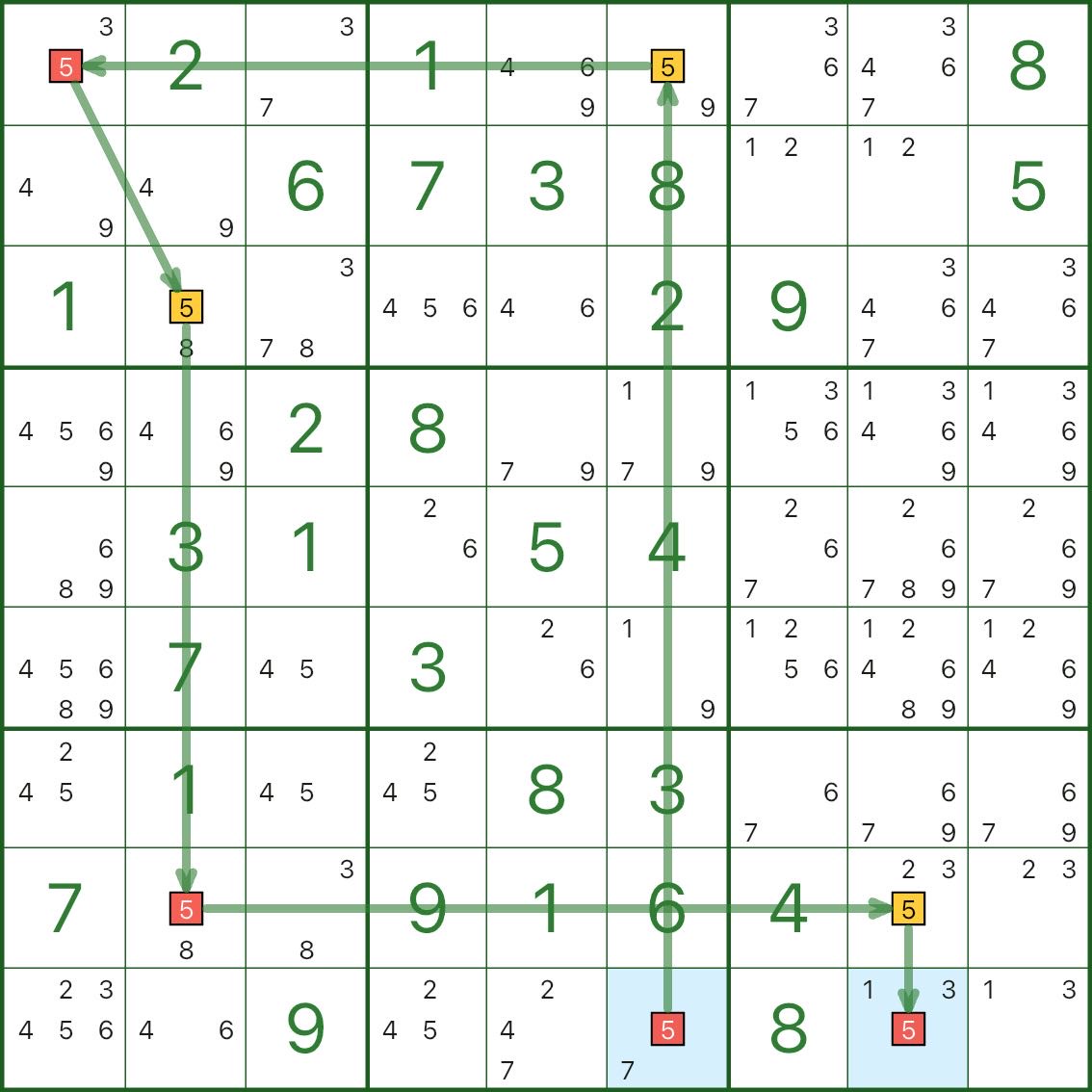
したがって、青いルートは不可能です。
青色の候補 5 はすべて除外できます (画像 4 を参照)。

---

基本的なカラーリングを見つける方法

1 行のチェックリスト: 二重位置の強いリンクを見つけて青/黄色に色付けし、トラップまたは同じ色の矛盾を探します。

実際のパズルでは:

1. 数字 d を選択してください
2. d の二重位置の強いリンクを見つけます (d の候補が 2 つだけあるユニット)
3. どこからでも始めて、強いリンクに沿って色を変えます
4. 以下を探します:
   • 青と黄色が 1 つずつ見える赤の候補 → トラップ除去
   • 1 つのユニット内の 2 つの同じ色の候補 → その色全体を削除