チェーンの基礎

強リンク / 弱リンク / 交互推論（AIC）

チェーンは、多くの上級数独テクニックの土台です。
本質はシンプルで、候補どうしの関係を 「もし A なら B」 の連鎖として追う推理です。

この章を理解すると、単数チェーン、Two-String Kite、Skyscraper、Medusa、AIC などのヒントが読みやすくなります。

本アプリではセル位置を r1c1 のように表します。
r = row（行）、c = column（列）

図では次の色分けを使います。

• 緑の実線: 強リンク
• 黄色の破線: 弱リンク
• 青/黄の候補背景: 交互の 2 状態を可視化
• 赤い候補: このステップで除外する候補

注意: チェーンは 双方向 です。矢印は読みやすさの補助です。

---

チェーンとは？

チェーンは、候補間の「真偽の伝播」をつないだ推理経路です。

A が成り立たないなら B が成り立つ
B が成り立つなら C は成り立たない
…

構成要素は次の 2 つです。

• ノード: セル内の候補（数字）
• リンク: 候補同士の関係（強リンク / 弱リンク）

チェーンのゴールは 2 パターンあります。

• 矛盾に到達: ある候補が偽だと証明できる → 除外
• 確定に到達: ある候補が真だと証明できる → 値を確定

この記事では、まず最も基本となる 単数チェーン（同じ数字 d だけを追うチェーン）を扱います。
（二値セルベースの関係や grouped link は後続記事で扱います）

---

強リンクと弱リンク

強リンク（共役ペア）

覚え方: どちらか一方は必ず真

同じ house（行 / 列 / ボックス）で、数字 d の候補が ちょうど 2 か所 のとき、その 2 候補は強リンクです。

重要な含意:

• A が偽なら B は真
• B が偽なら A は真

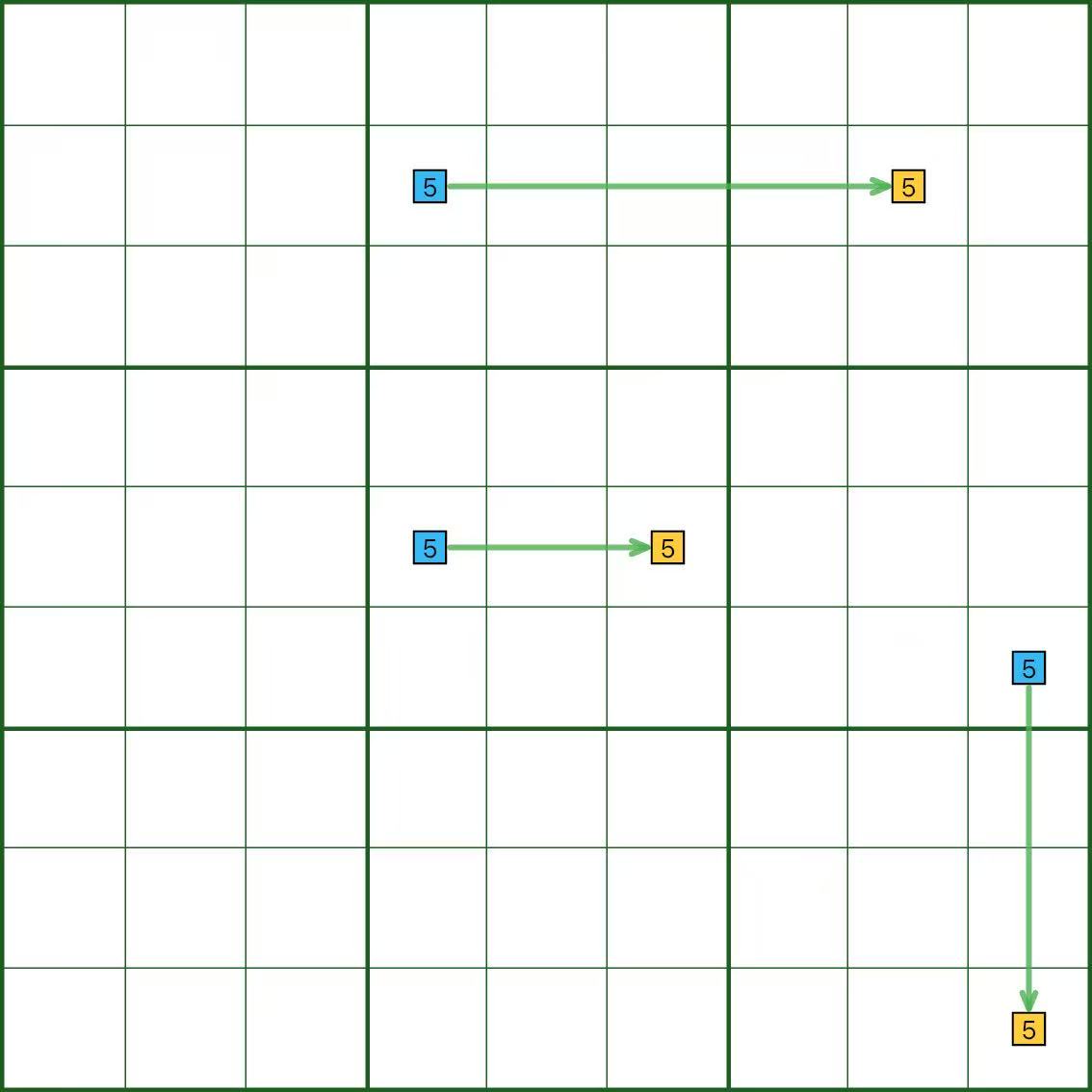
図では、数字 5 について行・列・ボックスの強リンクを示しています。

補足: 強リンクの 2 候補は同じ house 内にあるため、同時に真にはなれません。
つまり強リンクは「弱リンクの性質」も持ちます。

要約:

強リンク = 互いに同時真は不可 + 少なくとも一方は真

弱リンク

覚え方: 同時に真にはなれない

弱リンクが表すのは 1 つだけです。

2 候補は同時に真になれない

単数チェーンで最も典型なのは、同じ house 内の同じ数字 d の候補同士です。

含意:

• A が真なら B は偽

ただし逆は成り立ちません。

• A が偽でも B が真とは限らない（第三候補があり得る）

---

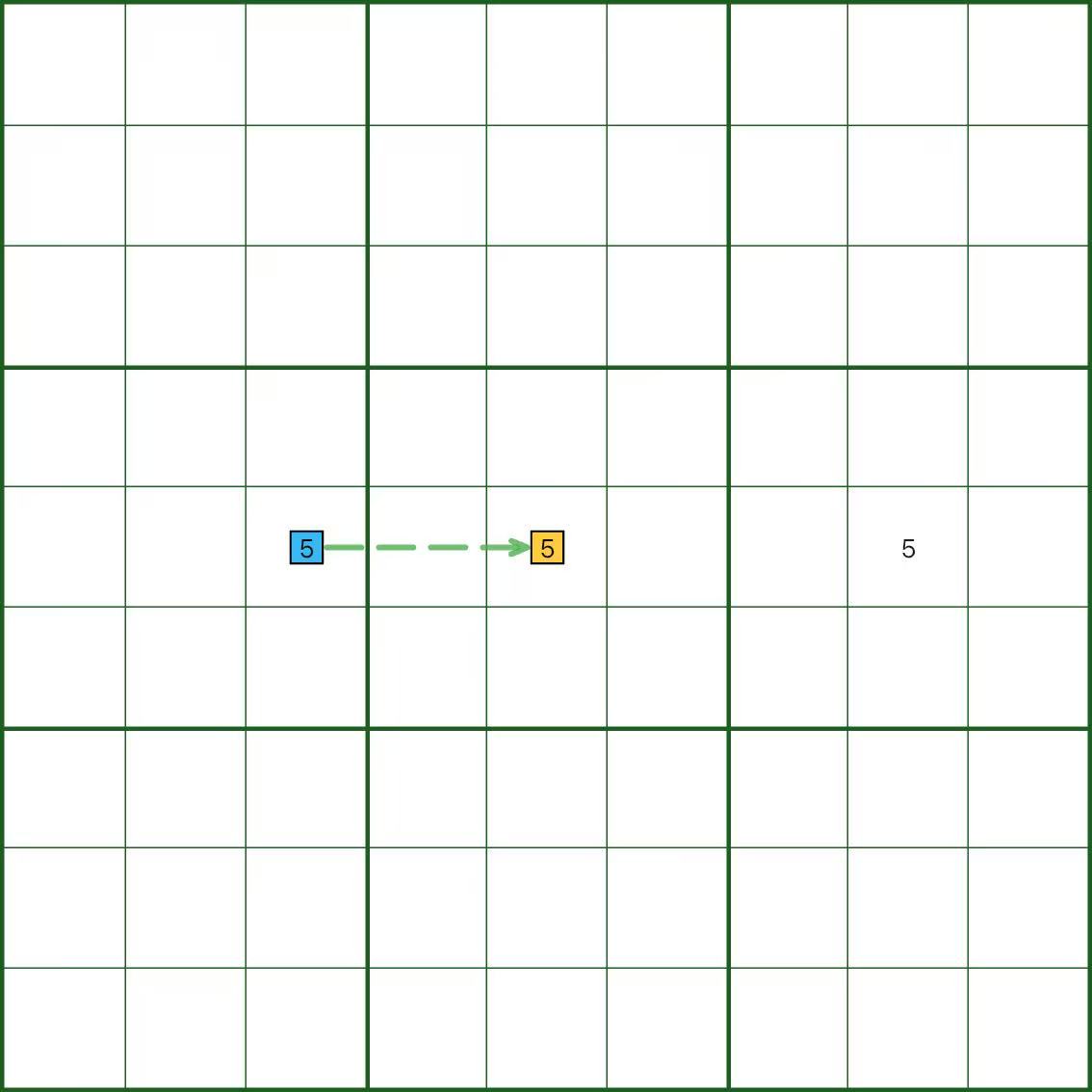
チェーンの伝播ルール

チェーンを読むときは次の 2 ルールを使います。

1. 真 →（弱リンク）→ 偽
2. 偽 →（強リンク）→ 真

そのため有効なチェーンは通常、次のように交互になります。

偽 —(強)→真—(弱)→偽—(強)→真—(弱)→偽…

なぜ交互が重要か:

• 弱リンクの両側を「偽→？」で進めることはできない
• 強弱を交互に使うと真偽が安定して伝播する

---

例

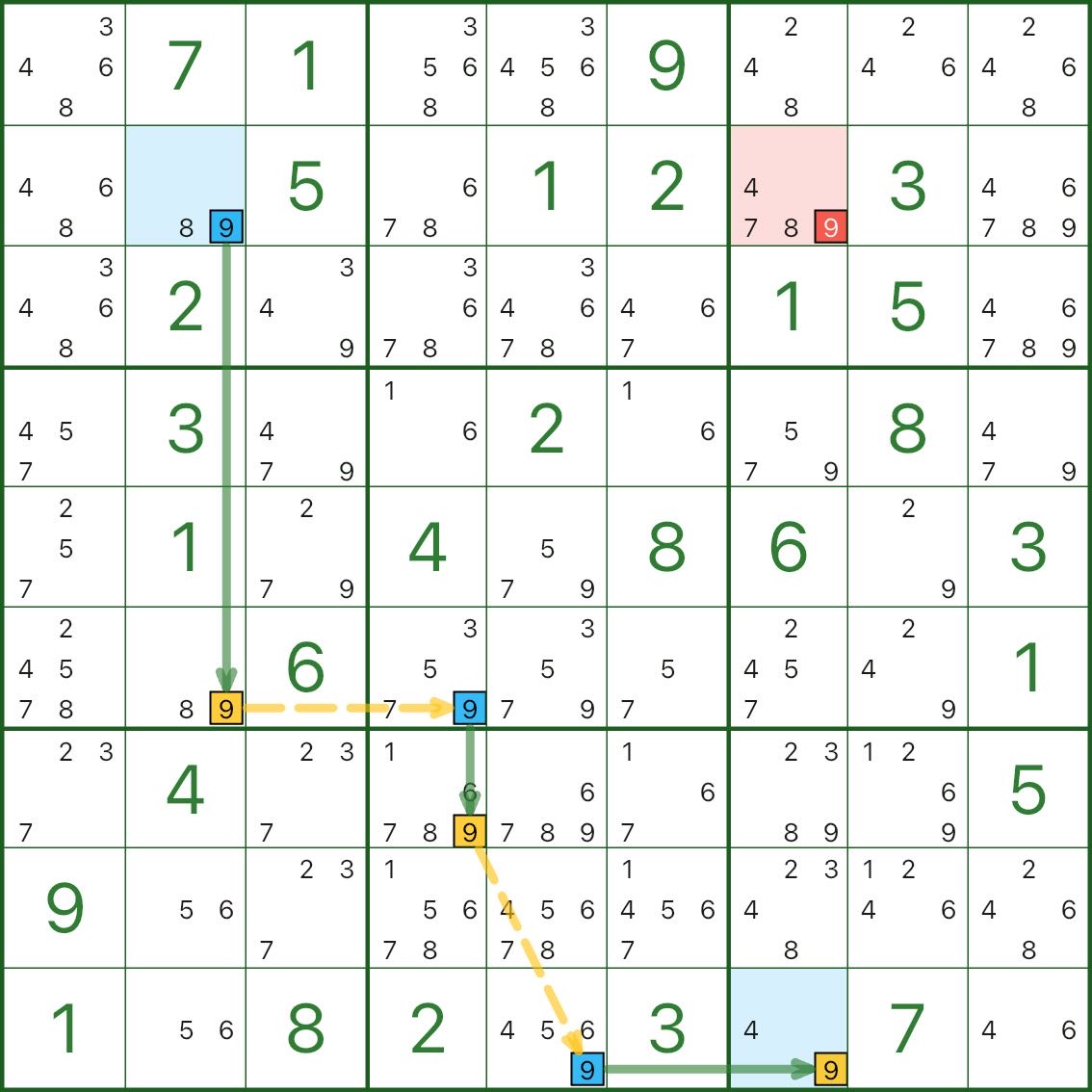
赤い候補は r2c7 の 9 です。

読み方:

1. ハイライト起点から、r2c2≠9 が入るとチェーンが伝播し、r9c7=9 が強制されます。
   （偽→真→偽→真→偽→真 の交互）

2. ここで反証を使います。赤候補 r2c7=9 を仮定すると:

   • 同じ行なので r2c2 は 9 になれない（r2c2(9) は偽）
   • その偽がチェーンで伝播して r9c7(9) が真になる
   • r2c7 と r9c7 は同じ列なので、同時に 9 は不可能 → 矛盾

したがって r2c7 の 9 は除外できます。

---

練習

次の 3 図はすべて単数チェーンです。

確認ポイント:

1. どこが強リンクか（なぜ「どちらか一方は真」なのか）
2. どこが弱リンクか（なぜ同時真が不可なのか）
3. 赤候補がなぜ矛盾に至るか

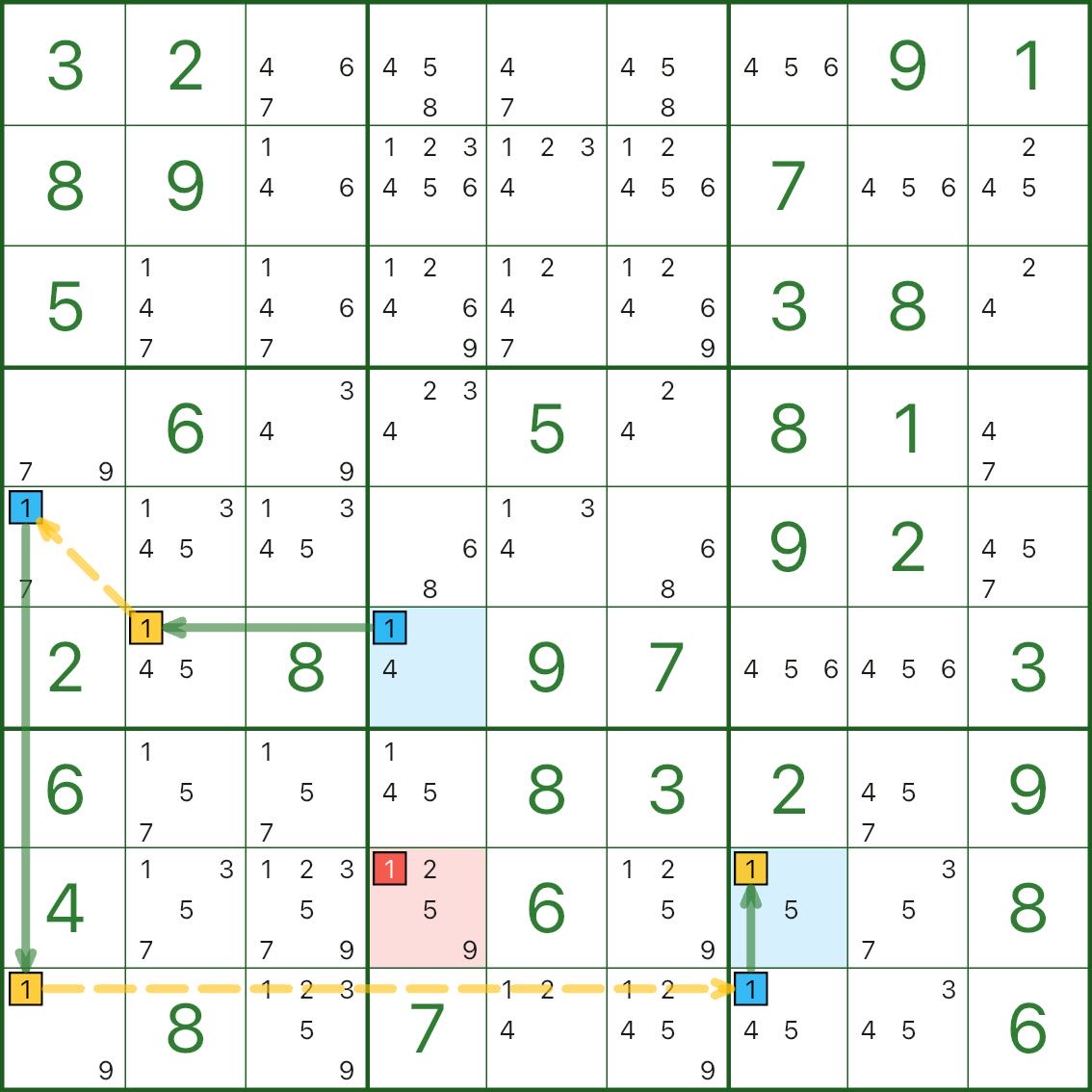
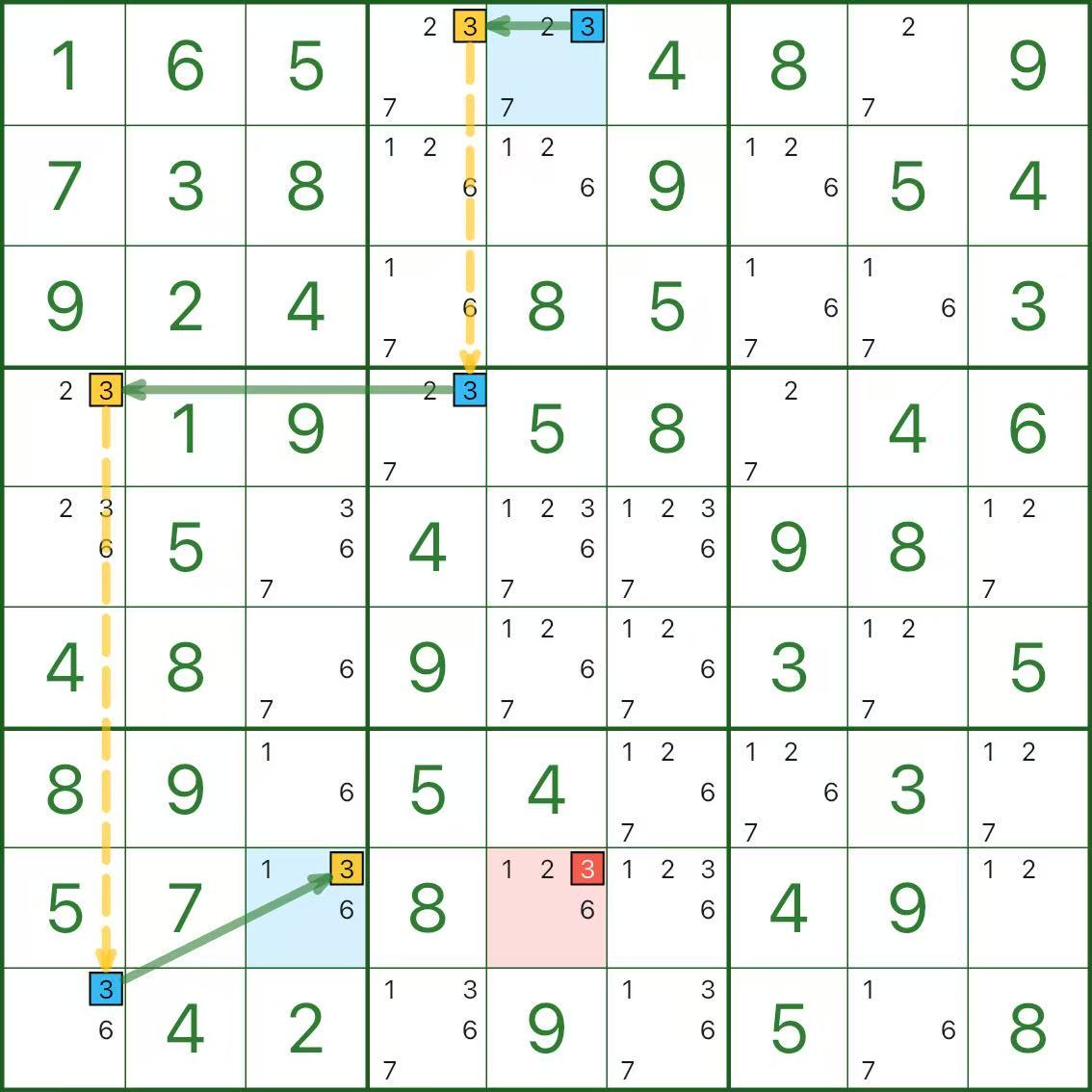
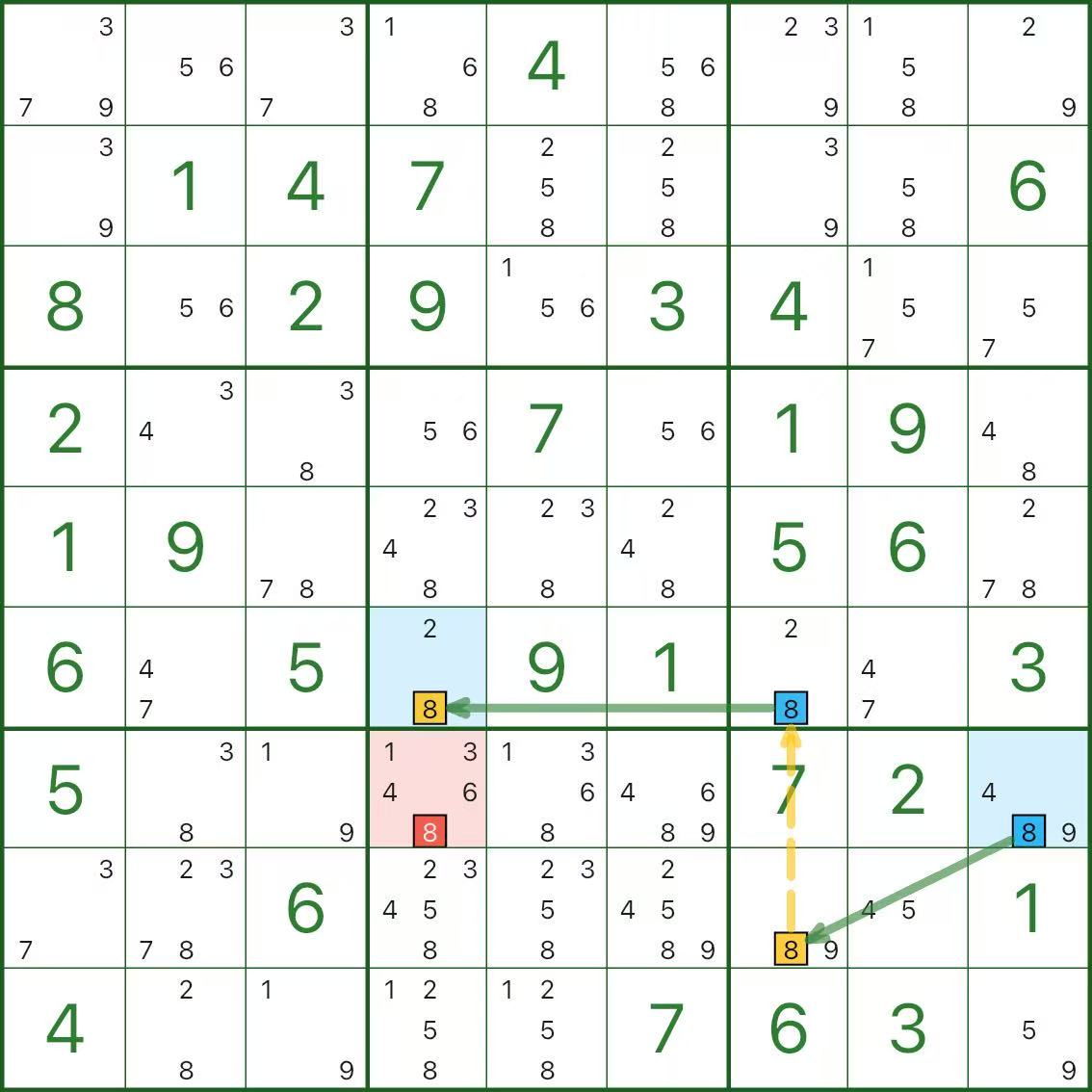
最初は難しく感じて普通です。
ここを理解すると、上級チェーン系テクニックの見通しが一気によくなります。