バグ+1

前提条件: BUG+1 は、正確に 1 つの解決策を持つパズルに依存しています。
まだ読んでいない場合は、ここから始めてください。
Uniqueness

---

1. 概要

BUG+1 は BUG + 1 の略です。Bivalue Universal Grave + 1 とも呼ばれるかもしれません。

名前は恐ろしく聞こえますが、非常に具体的なボードの状態を表しています。

• ほぼすべての未解決セルは bivalue (候補は 2 つだけ)
• 1 つの「例外セル」には 3 つの候補があります (これは「+1」です)

バグとは何ですか?

BUG = 二値ユニバーサル墓。

これが「墓場」と呼ばれるのは、グリッドが「行き詰まっている」と感じる可能性があるためです。候補はどこでもペアで登場し、独自性がなければ進歩が停滞することがよくあります。

グリッドがこれら 2 つの条件を満たす場合、非常に対称的な「バグ」構造になります。

1. すべての未解決のセルは 2 値です
2. 任意の数字 d について、すべてのハウス (行/列/ボックス) で、d の候補位置の数は 偶数
   • 最も一般的なのは 2
   • d がすでにその家に配置されている場合は、0 にすることができます (それでも偶数)

この対称性により、多くの場合、2 の有効な補完 (複数の解) が可能になります。

それで、BUG+1 とは何ですか?

BUG+1 は「ほぼバグですが、完全ではありません」:

• すべての未解決のセルは 2 値です
  候補が 3 つある 1 つのセルを除く

その余分な候補は均等な対称性を破ります。そしてそれこそが、一意性を利用して配置を強制できるのです。

したがって、例外セルには強制候補が 1 つあります。数字を直接配置できます。

---

2. ウォークスルー

ステップ 1: 「ほぼすべてが 2 値」状態を特定します (上の画像)

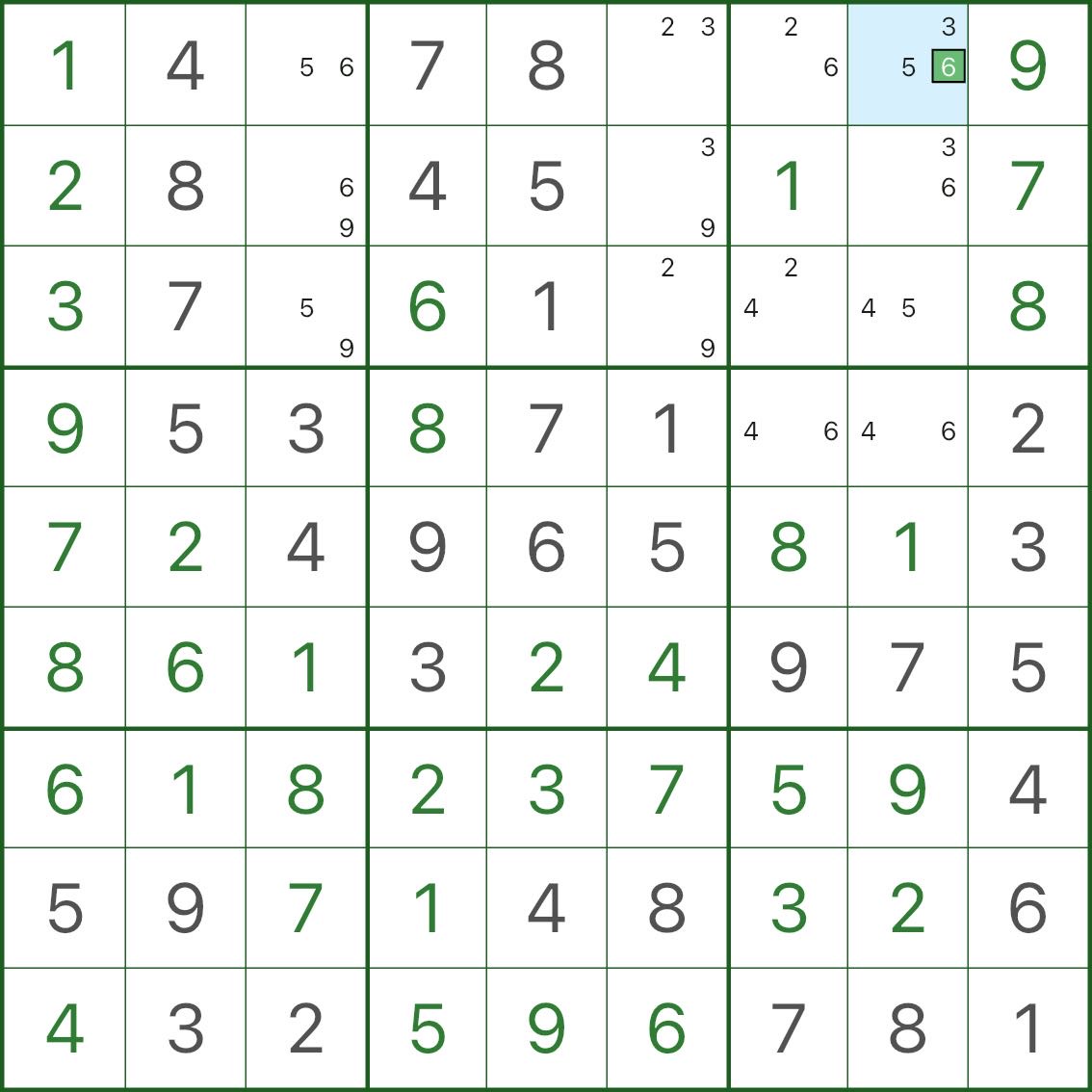
画像の場合:

• ほとんどの空のセルには 2 個の小さな候補のみが表示されます
• 1 つのセルは例外で、3 の候補 (「+1」) が表示されます。

ステップ 2: どの桁を入力する必要がありますか? （そしてなぜ？）

例外セル内の 3 つの候補だけに焦点を当て、奇数と偶数をチェックするという 1 つの単純な作業を実行します。

方法:

1. 例外セル内の 3 つの候補を確認します。
2. これらの各桁について、例外セルの 行/列/ボックス に候補として表示される回数を数えます。

通常、これらのハウスの 1 つに 1 つの数字が 3 回 (奇数) 出現していることがわかります。
その「奇数」の候補が、配置すべき数字です。

なぜ？矛盾を使用します。

この「奇数」の候補を配置せず、代わりに他の 2 つの「偶数」候補の 1 つを選択すると仮定します。

1. 例外セルが 2 値になります
2. ハウス間の候補分布が「均等な」対称性に戻ります (BUG 構造)
3. BUG 構造では、2 の有効な補完が許可されることがよくあります (複数の解決策)

しかし、パズルはユニークでなければならないため、その選択は不可能です。
したがって、「奇数」の候補は真である必要があります。それは、配置した数字です。

何もカウントしたくない場合は、ヒントによって強制候補が強調表示されます。

---

3. 例

下の画像は結果を示しています。例外セルに強制的に「+1」候補が配置されます。

---

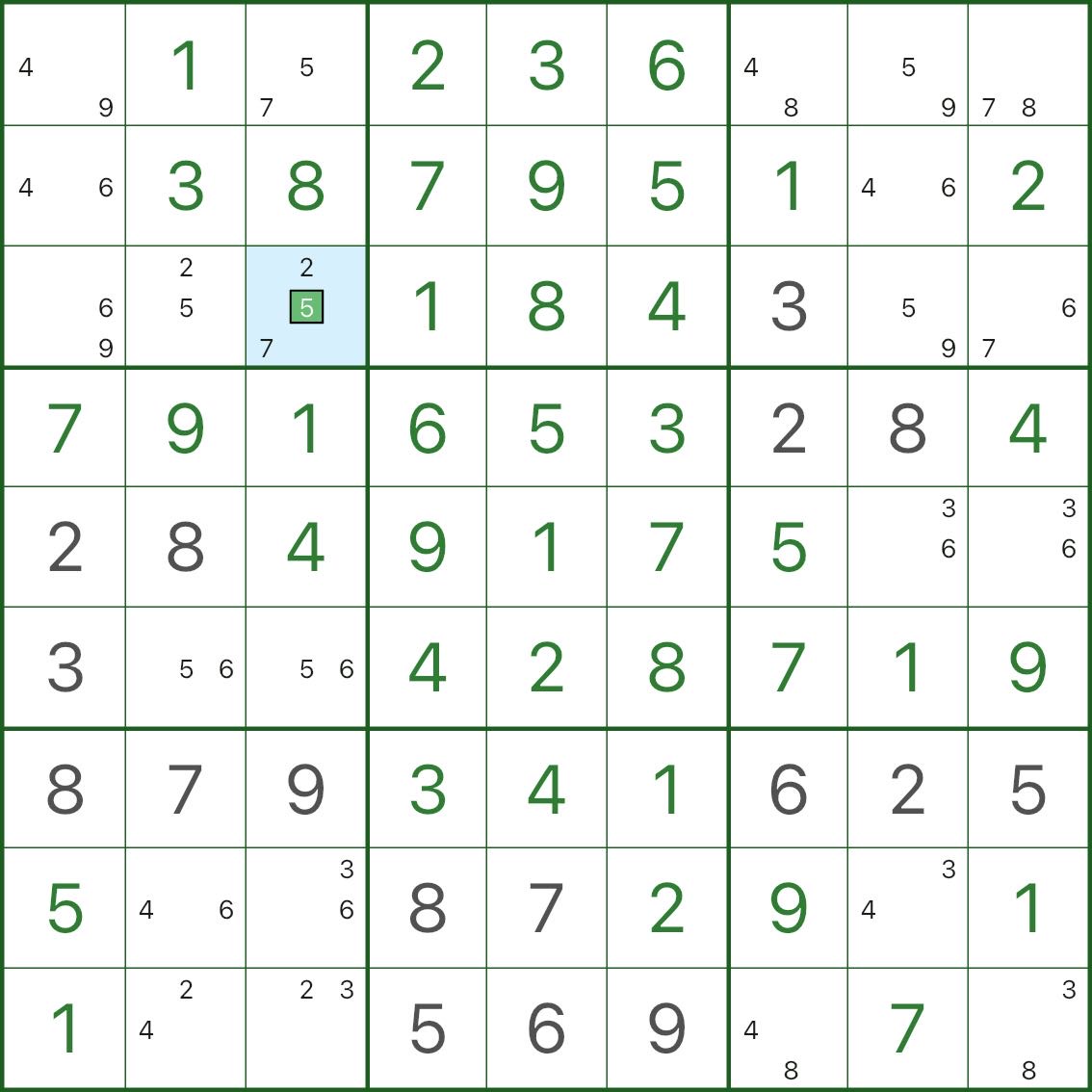
4. BUG+1 を見つける方法

このチェックリストを使用してください。

1. 候補のメモが完全で信頼できるものであることを確認します (必要に応じて完全な候補を生成します)。
2. 次のようなグリッドを探します。
   • すべての未解決のセルは 2 値です
   • ちょうど 1 つのセルに 3 つの候補があります
3. そのセルの行/列/ボックスで、これら 3 つの数字の出現候補を数えます。奇数 の数字 (通常は 3) が強制数字です。
4. ヒントは例外セルを強調表示し、どの候補が強制されるかを示します。

注: BUG+1 は 一意性ベース テクニックです。パズルの解決策が 1 つであることが保証されている場合にのみ適用されます。