ボックスの削除

ボックス消去は、非常に一般的な「候補消去」手法です。次のように覚えることができます。

ボックスと線の交点で数字が「ロック」されている場合、反対側にはその数字を含めることはできません。

r1c1 を使用してセルの位置を記述します: r = 行、c = 列。

ヒント: 以下の画像では、緑色のセルは「ロックされた位置」を示し、赤色の候補はこの手順で削除できる候補です。

---

例 1: 列は数字を 1 つのボックスにロックします (そのボックス内の赤い候補を削除します)

まず、下の画像を見てください。強調表示されている 列 4 と 2 つの緑色のセル r8c4 および r9c4 に注目してください。
列 4 では、数字 6 がこれら 2 つの緑色のセルにのみ表示されていることがわかります。

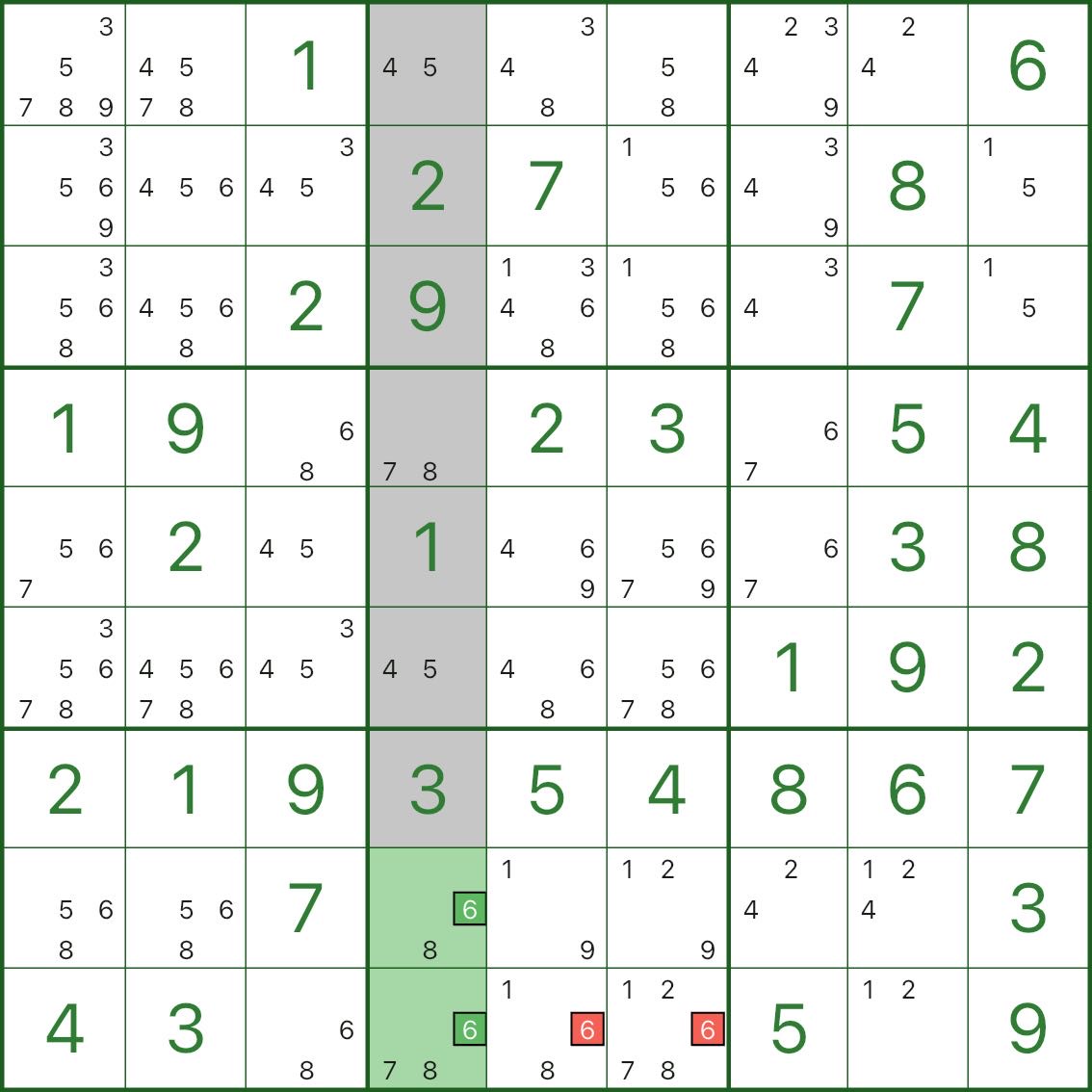
これは、列 4 の 6 はボックス 8 に配置する必要があります (r8c4 と r9c4 は両方ともボックス 8 にあるため) を意味します。

ここで、ボックス 8 内の赤い 6 候補を見てください。これらは削除できます。
矛盾による簡単な証明:

• ボックス 8 の赤い位置の 1 つが実際には 6 であると仮定します。
• その場合、r8c4 と r9c4 (同じボックス内) を 6 にすることはできません。
• しかし、その場合、列 4 には数字 6 を入れる場所が残らないことになります — 矛盾
  ⇒ ボックス 8 の赤 6 の候補は不可能なので、削除できます。

---

例 2: ボックスは数字を 1 つの行にロックします (その行の赤い候補を削除します)

まず、下の画像を見てください。強調表示された ボックス 2 と 2 つの緑色のセル r1c4 および r1c5 に注目してください。
ボックス 2 では、数字 9 が 2 つの緑色のセルにのみ表示されていることがわかります。

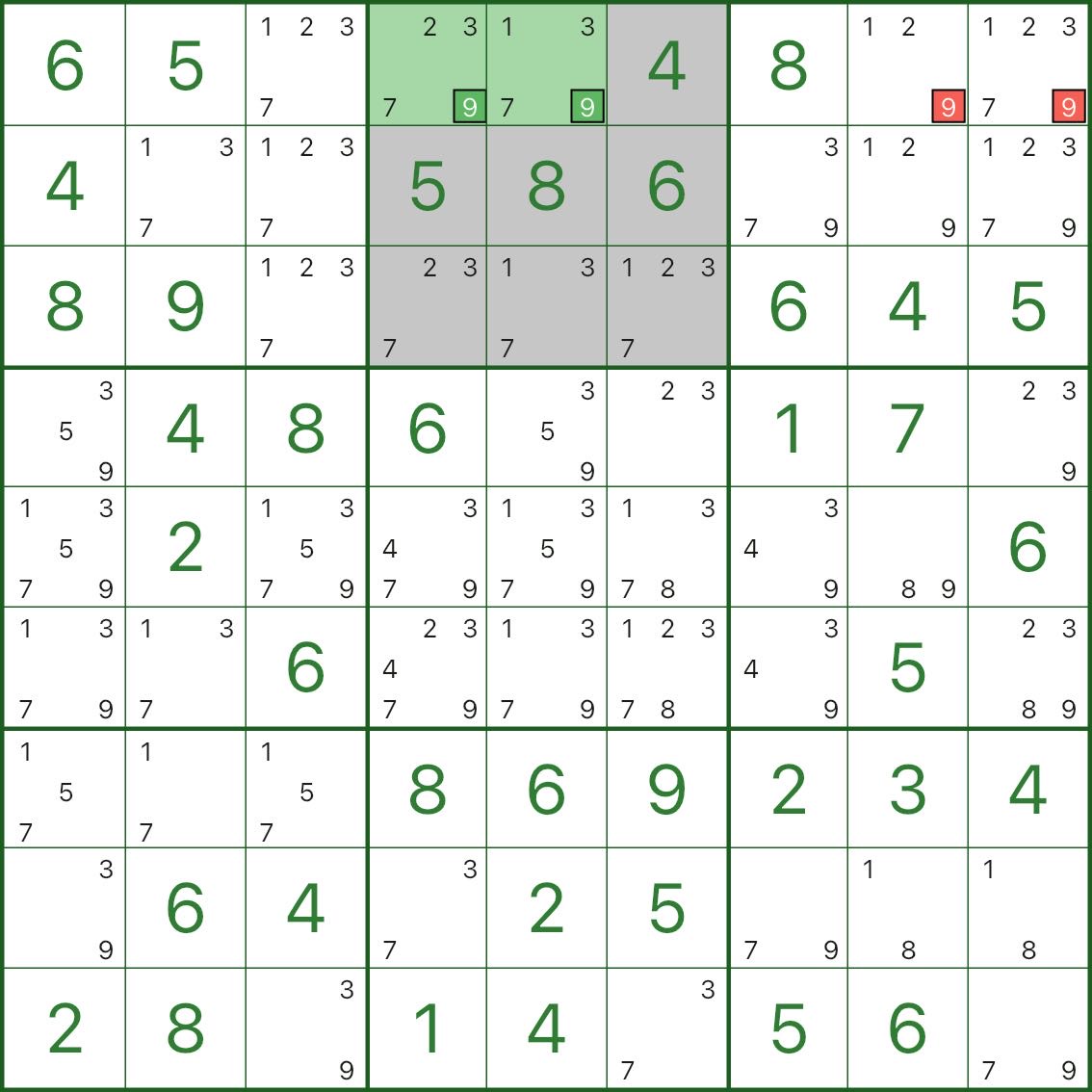
したがって、ボックス 2 の 9 は r1c4 または r1c5 でなければなりません。
そして、両方とも行 1 にあるため、行 1 の他の場所にある赤い 9 候補は削除できます。

• 行 1 の他のセルが 9 であると仮定します。
• r1c4 と r1c5 (同じ行) を 9 にすることはできません
• しかし、その場合、ボックス 2 には数字 9 を置く場所がありません — 矛盾します
  ⇒ 1行目の赤9の候補は不可能なので削除可能

---

概要

余分な名前を覚える必要はありません。次の 2 つの「方向」を覚えておいてください。

• 行/列からボックスへ: 行内の数字のすべての候補が 1 つのボックス内に収まる場合、その数字をボックスの残りの部分から削除します。
• ボックスから行/列へ: ボックス内の数字のすべての候補が 1 つの行/列内に収まる場合、行の残りの部分からその数字を削除します。