直接除外

直接除外は、最も信頼できる種類の数独推論です。
数字を選択し、行/列/ボックス内でその数字が入力できる唯一の場所を見つけます。

説明できる範囲で:

「他の場所はすべて競合するでしょう」

そうすれば確実な動きを手に入れることができます。

このガイドでは、r2c5 を使用してセルを参照します。
r = 行、c = 列。

---

例 1: 列の除外 (列 5 に 8 を配置)

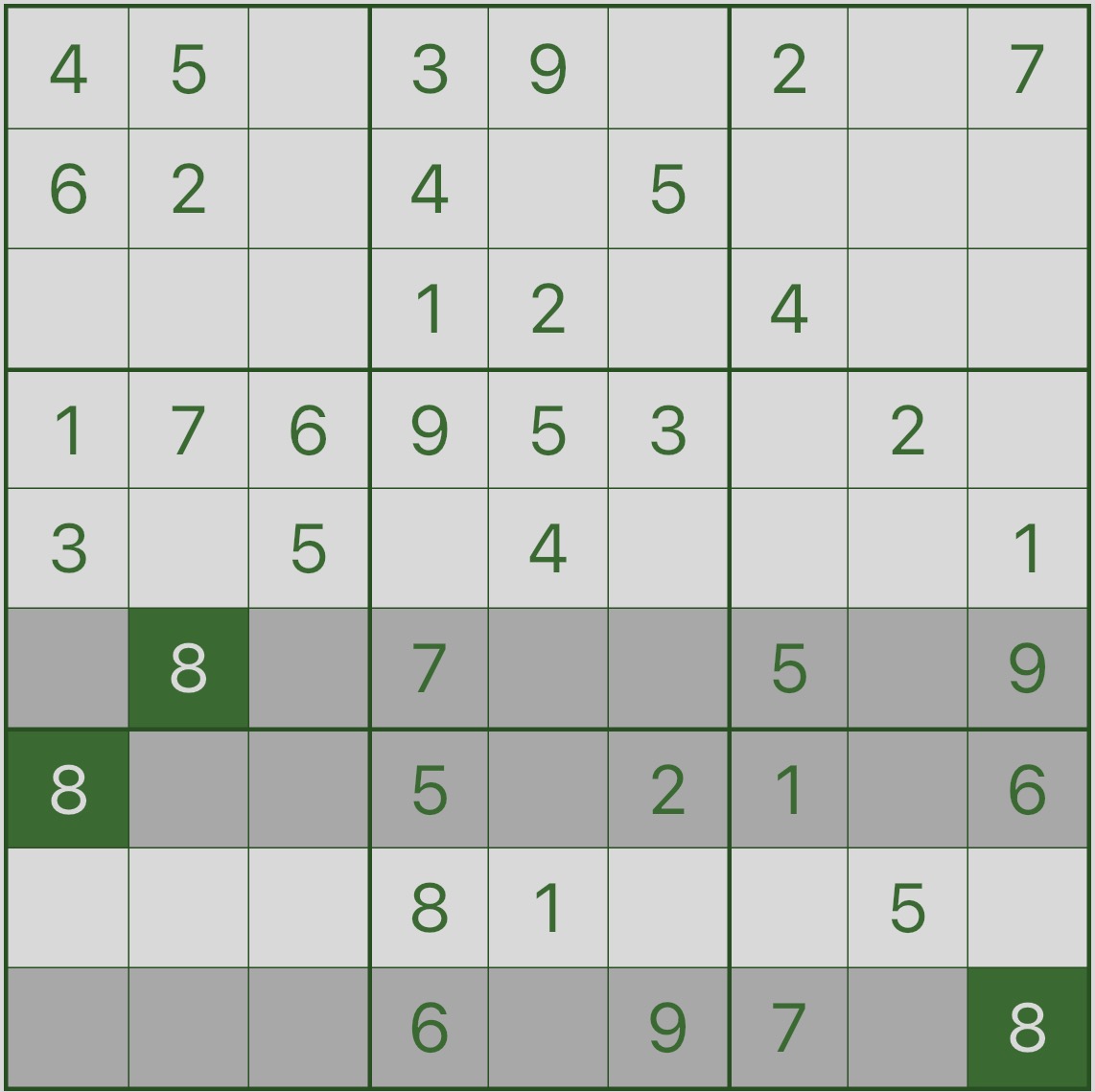
画像 1 を見て、強調表示された領域と強調表示された 8 に注目してください。
強調表示された行にはすでに 8 が含まれていることがわかります。

ここで画像 2 を見てください。列 5 のみに注目します。
この列には空のセルがいくつかありますが、その行にはすでに 8 が含まれているため、8 になることはできません。

• r6c5 はすでに 8 を含む行にあります → r6c5 を 8 にすることはできません
• r7c5 はすでに 8 を含む行にあります → r7c5 を 8 にすることはできません
• r9c5 はすでに 8 を含む行にあります → r9c5 を 8 にすることはできません

これにより、列 5 の 8 の有効なスポットとして r2c5 のみが残ります。
したがって、r2c5 = 8 と置くことができます。

---

例 2: ボックスの除外 (ボックス 1 に 1 を配置)

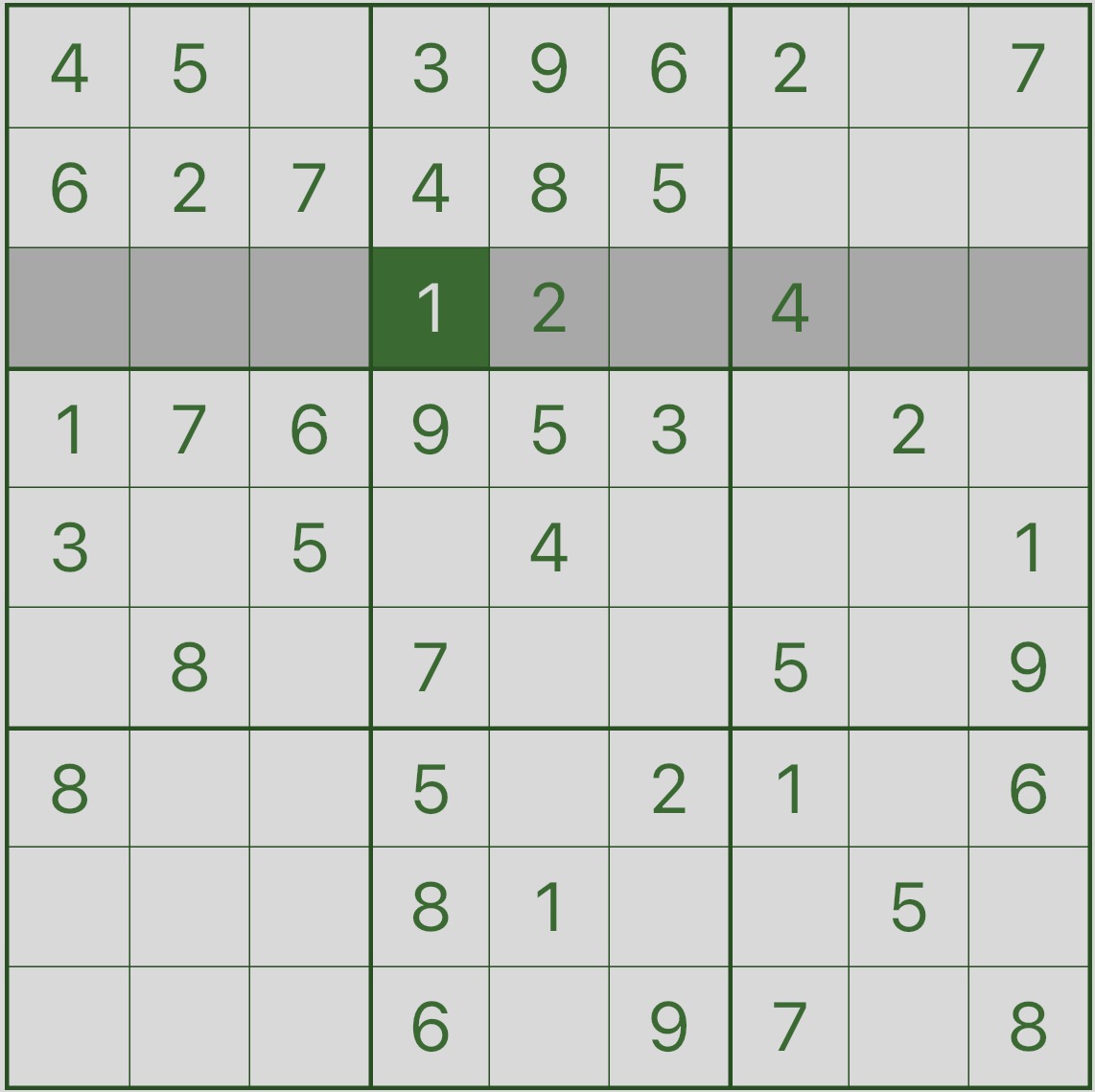
画像 3 を見て、強調表示されている 1 に注目してください。
これにより、行 3 にはすでに 1 が含まれていることがわかります。

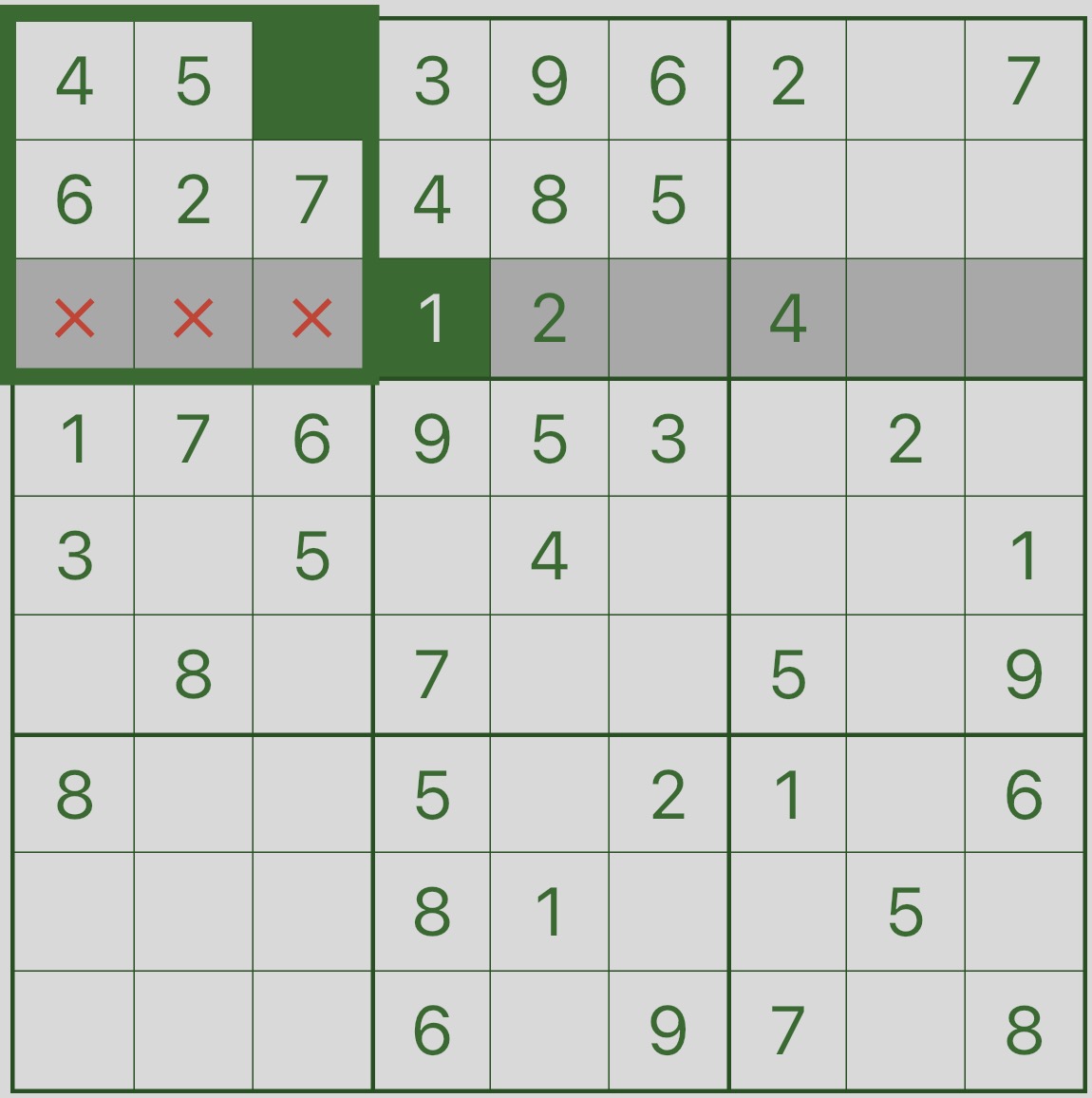
次に、画像 4 を見て、ボックス 1 (左上の 3×3 ボックス) に注目してください。
このボックスの下部 3 つのセル (r3c1、r3c2、r3c3) はすべて行 3 にあり、行 3 にはすでに 1 が入っているため、どれも 1 になることはできません。

したがって、このボックスに 1 が入る唯一の場所は r1c3 です。
したがって: r1c3 = 1。

---

テイクアウト

直接の除外は次のように考えてください。

「数字を選択し、すべての矛盾を除外します。最後に残った場所が答えです。」