AIC (スタンダードチェーン)

前提条件: Chain basics

---

1. 概要

AIC (Alternating Inference Chain) は、「最も一般的な」種類のチェーンです。

• X-Chain (行/列/ボックス内の 1 桁の強いリンク) と XY-Chain (または 2 値セル内) の構成要素を混合できます。
• チェーンが強い/弱いを交互に繰り返す限り、推論は伝播します。

最も一般的な使用法は消去です。
AIC が 2 つのエンドポイントが 両方とも偽であることはできないことを暗示している場合、両方のエンドポイントを 偽 にする候補はすべて真であることができないため、除外できます。

---

2. ウォークスルー

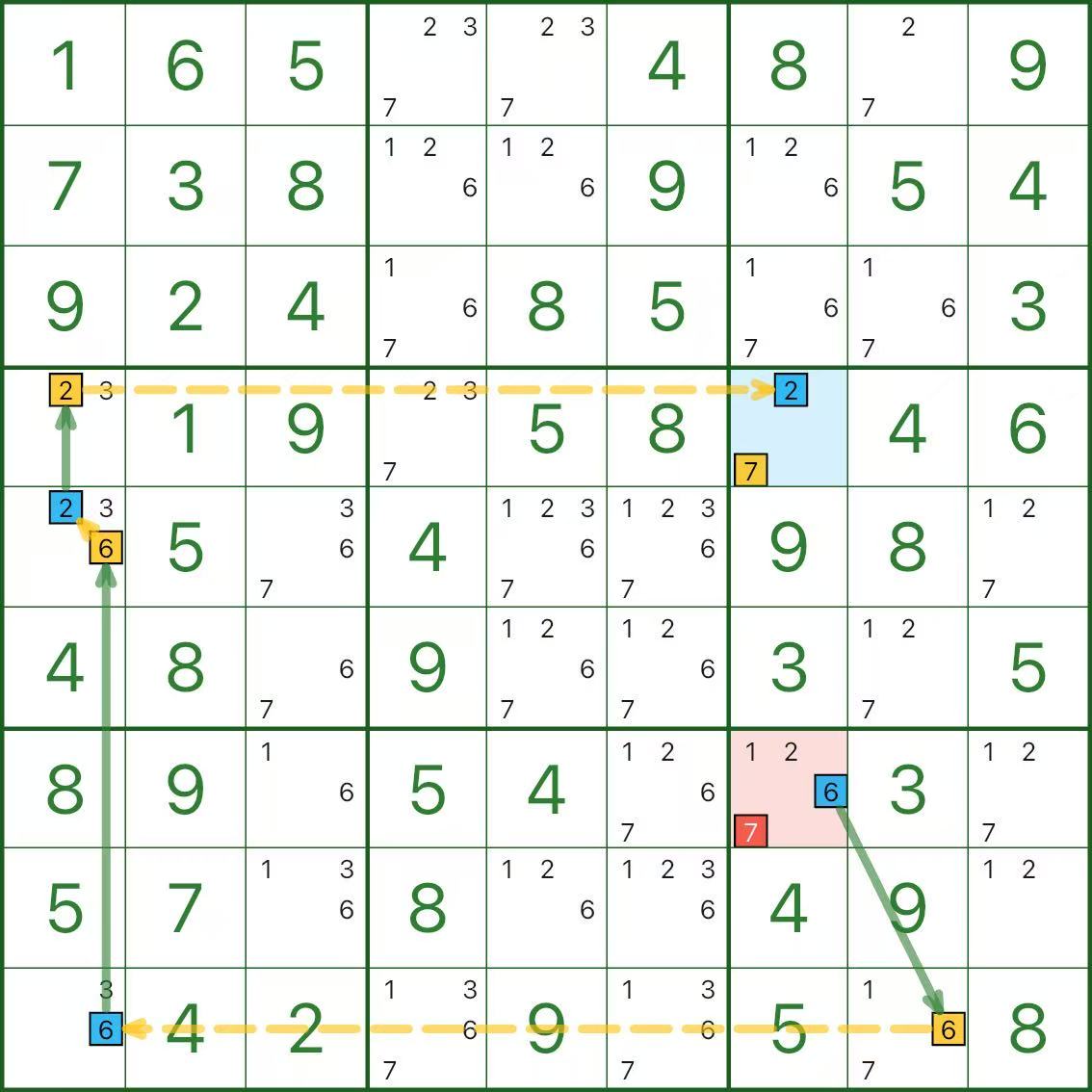
画像の場合:

• 2 つのエンドポイントは r7c7 の候補 6 と r4c7 の候補 7 (青)
• 除外は r7c7 の候補 7 (赤)
• r7c7 はエンドポイントであり、除去セルでもあるため、赤い背景で強調表示します。

なぜ r7c7の7 を削除できるのでしょうか?短い矛盾で十分です。

1. 重要な事実: 強い/弱い交互のチェーンでは、一方のエンドポイントが偽の場合、推論が伝播し、最終的にはもう一方のエンドポイントを真に強制します。
   したがって、2 つのエンドポイントを 両方とも偽にすることはできません (少なくとも 1 つは真である必要があります)。

2. 次に、赤色の候補 r7c7 = 7 が真であると仮定します。

   • 同じセル ⇒ r7c7 の候補 6 は 偽
   • 同じ列 ⇒ r4c7 の候補 7 は 偽

3. これにより両方のエンドポイントが偽になり、ステップ 1 と矛盾します。

したがって、r7c7 の候補 7 は除外できるという仮定は不可能です。

---

3. 例

さらに 2 つの AIC の例を次に示します。まずパターンを見つけてみてください。

• 青色のエンドポイント
• 強いリンクと弱いリンクを交互に繰り返す
• 両方のエンドポイントと競合する赤色の候補

---

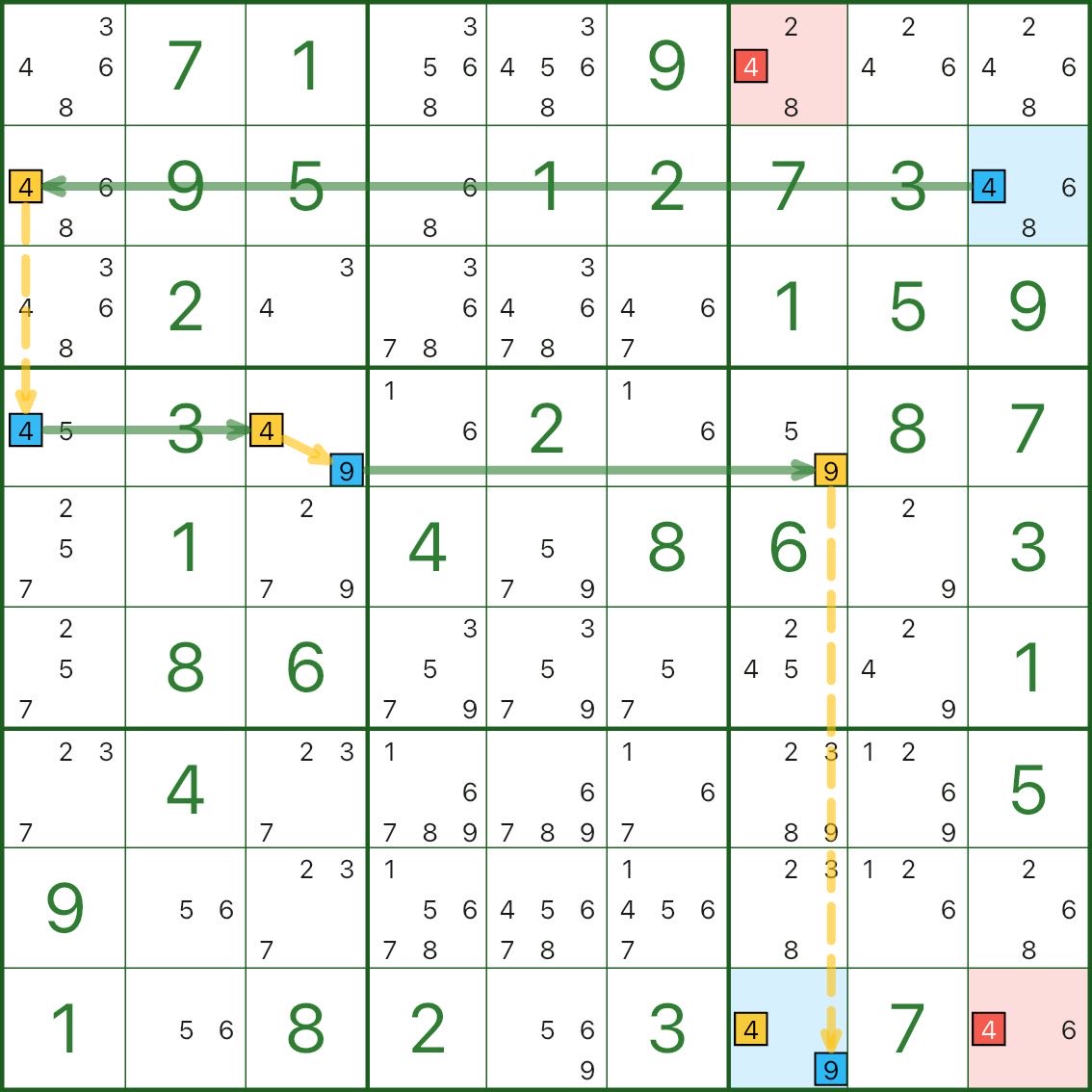
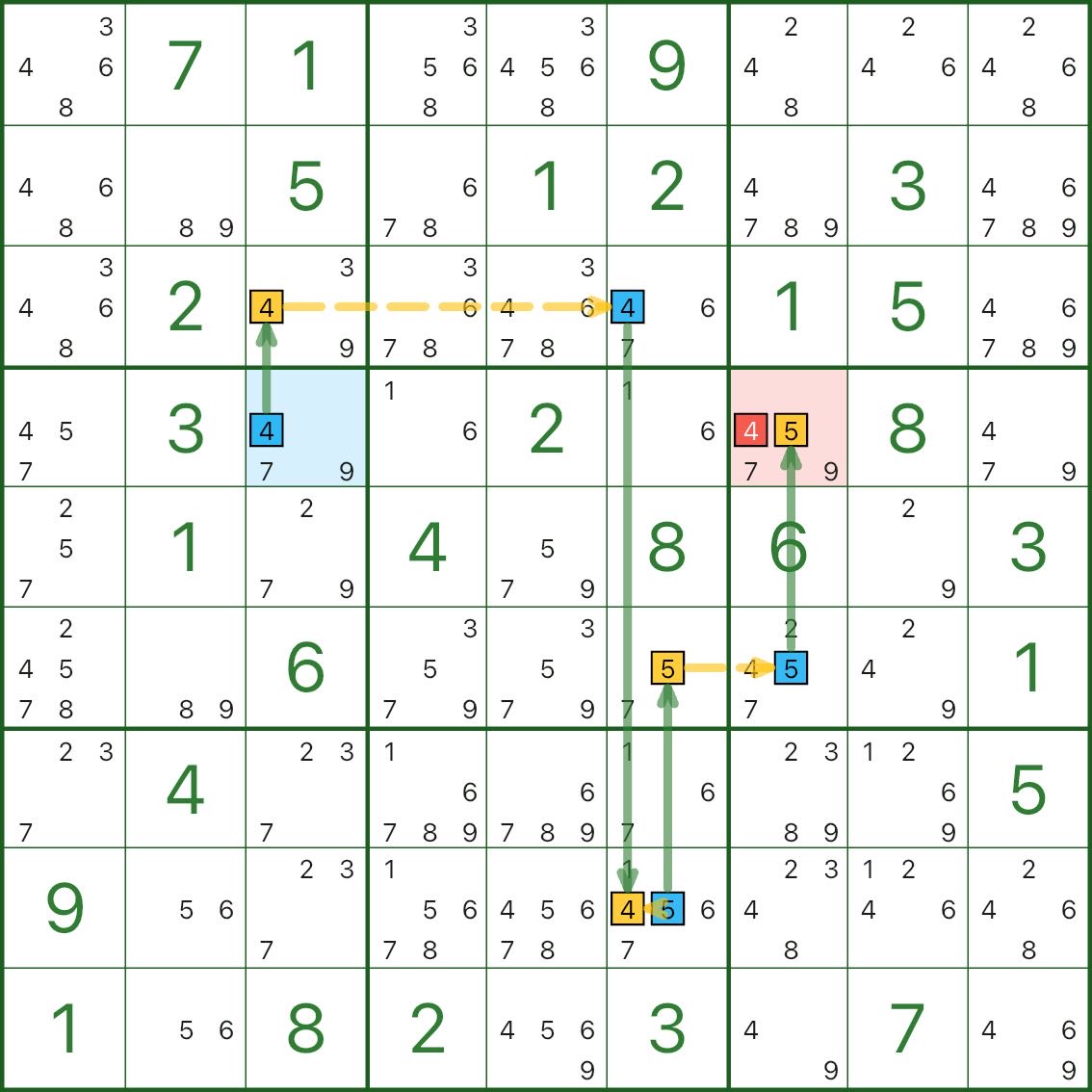
4. AIC を特定する方法

一文で表すと: 強リンク セグメントと二重値セグメントを交互のチェーンに接続し、両方のエンドポイントを強制的に偽にする候補を探します。

実践的なチェックリスト:

1. 強いリンクのソースを検索します (緑色の実線):
   • 数字の行/列/ボックス内にちょうど 2 つの候補があります (共役ペア)
   • または、二値セルはセル内に「X または Y のいずれか」の強いリンクを与えます
2. それらを弱いリンク (黄色の破線) で接続します。
   • 同じ桁の競合 (同じ行/列/ボックス)
   • 同じセル内の異なる数字
3. 強弱交互パターンを維持する
4. 赤の除外を探します: 両方のエンドポイントと競合する候補