XY-Aile

Description

XY-Wing (également connu sous le nom de Y-Wing) est une courte chaîne d'élimination des candidats composée d'un pivot et de deux ailes.

Sa forme ressemble à ceci :

• Pivot (bleu) : exactement deux candidats x, y
• Ailes (jaunes) : {x, z} et {y, z}

Conclusion : toute cellule qui peut voir les deux ailes ne peut pas contenir z, donc le candidat z peut y être éliminé.

---

Explication

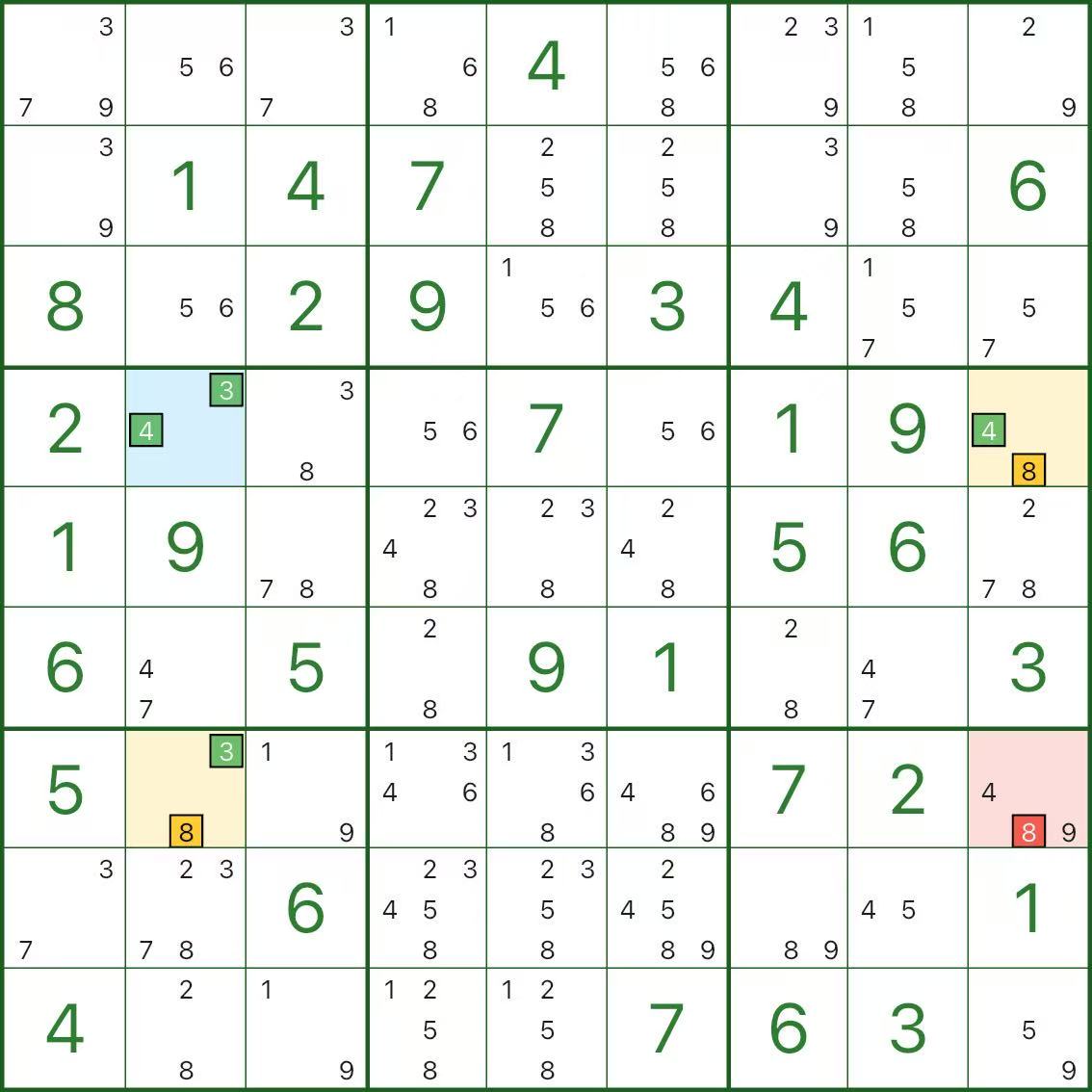
Dans l'image ci-dessus, nous souhaitons éliminer le candidat 8 en r7c9 (rouge).
Le pivot bleu est r4c2, avec les candidats 3 et 4.
Les deux ailes jaunes sont :

• r4c9 : candidats 4 et 8
• r7c2 : candidats 3 et 8

Pourquoi pouvons-nous supprimer 8 de r7c9 ? Une courte contradiction suffit :

• Supposons r7c9 = 8 (le candidat rouge est vrai)
• r7c9 peut voir les deux ailes, donc 8 est éliminé des deux ailes :
  • r4c9 doit être 4
  • r7c2 doit être 3
• Maintenant le pivot r4c2 est bloqué :
  • r4c9 = 4 ⇒ r4c2 ne peut pas être 4 (même ligne)
  • r7c2 = 3 ⇒ r4c2 ne peut pas valoir 3 (même colonne)
  • r4c2 n'avait que {3,4} ⇒ aucune valeur ne correspond (contradiction)

L'hypothèse est donc impossible : r7c9 ne peut pas être 8, et le candidat 8 peut être éliminé.

---

Exemples

Ces images montrent plus de motifs XY-Wing. Essayez de repérer la même structure : pivot (bleu) / deux ailes (jaune) / élimination (rouge).

---

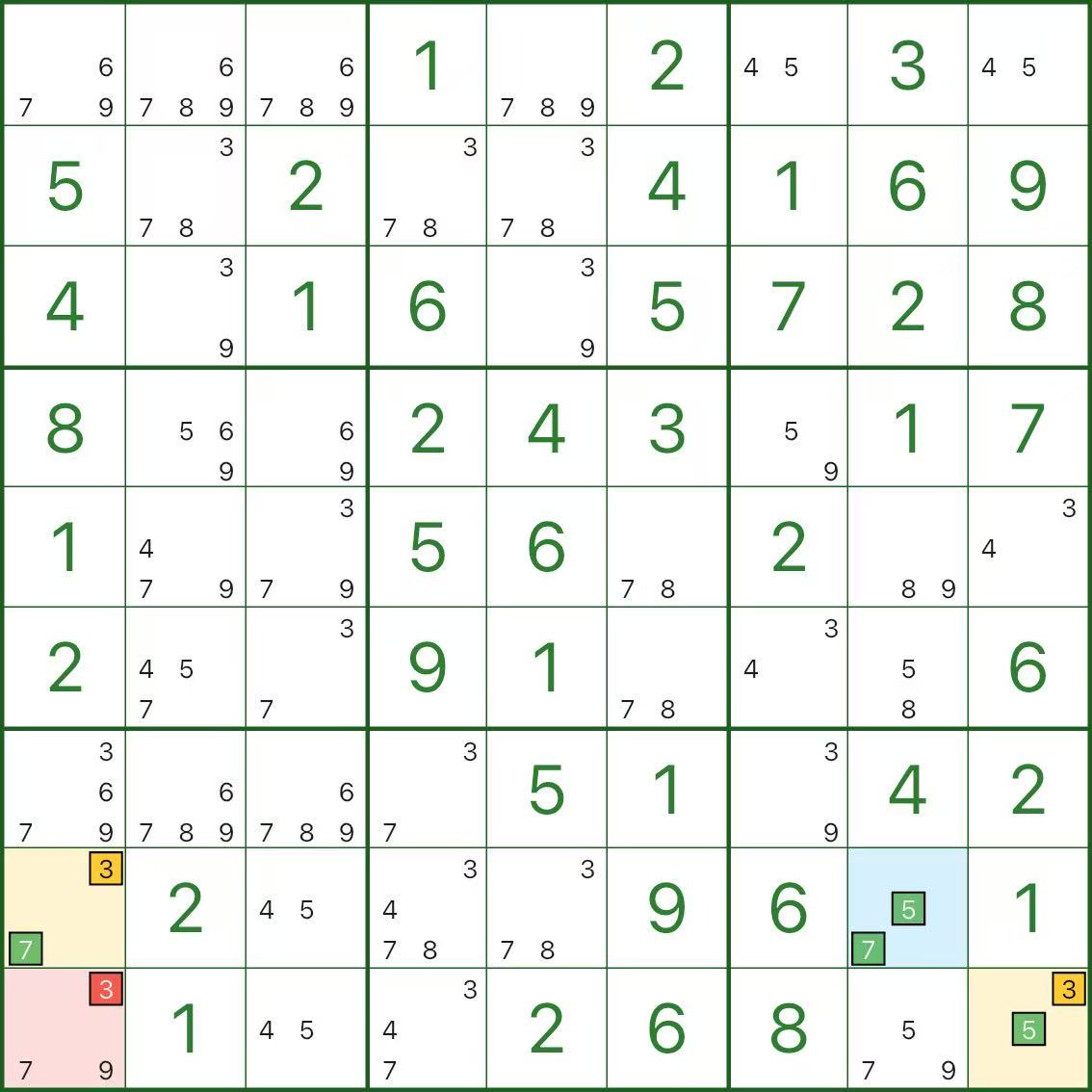
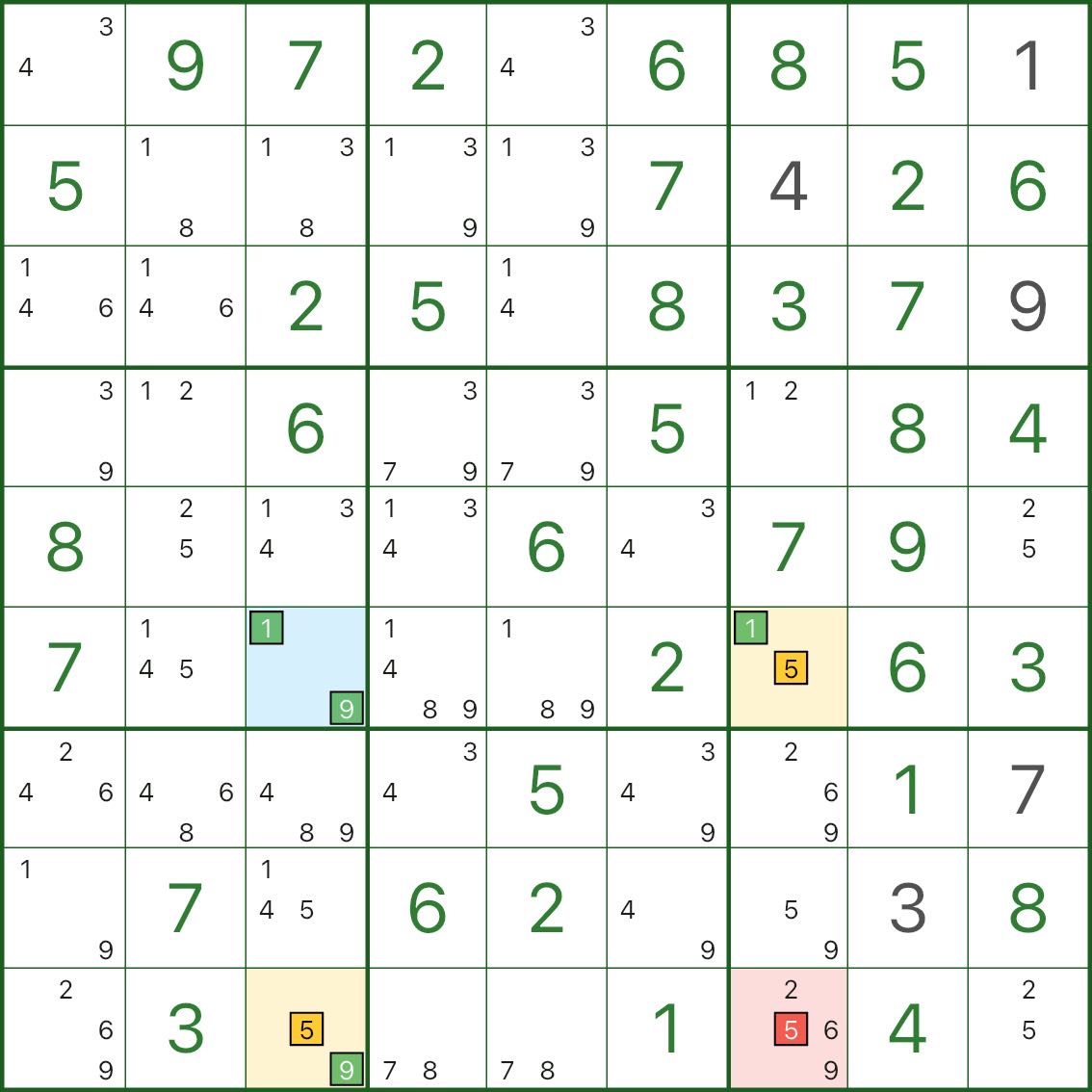
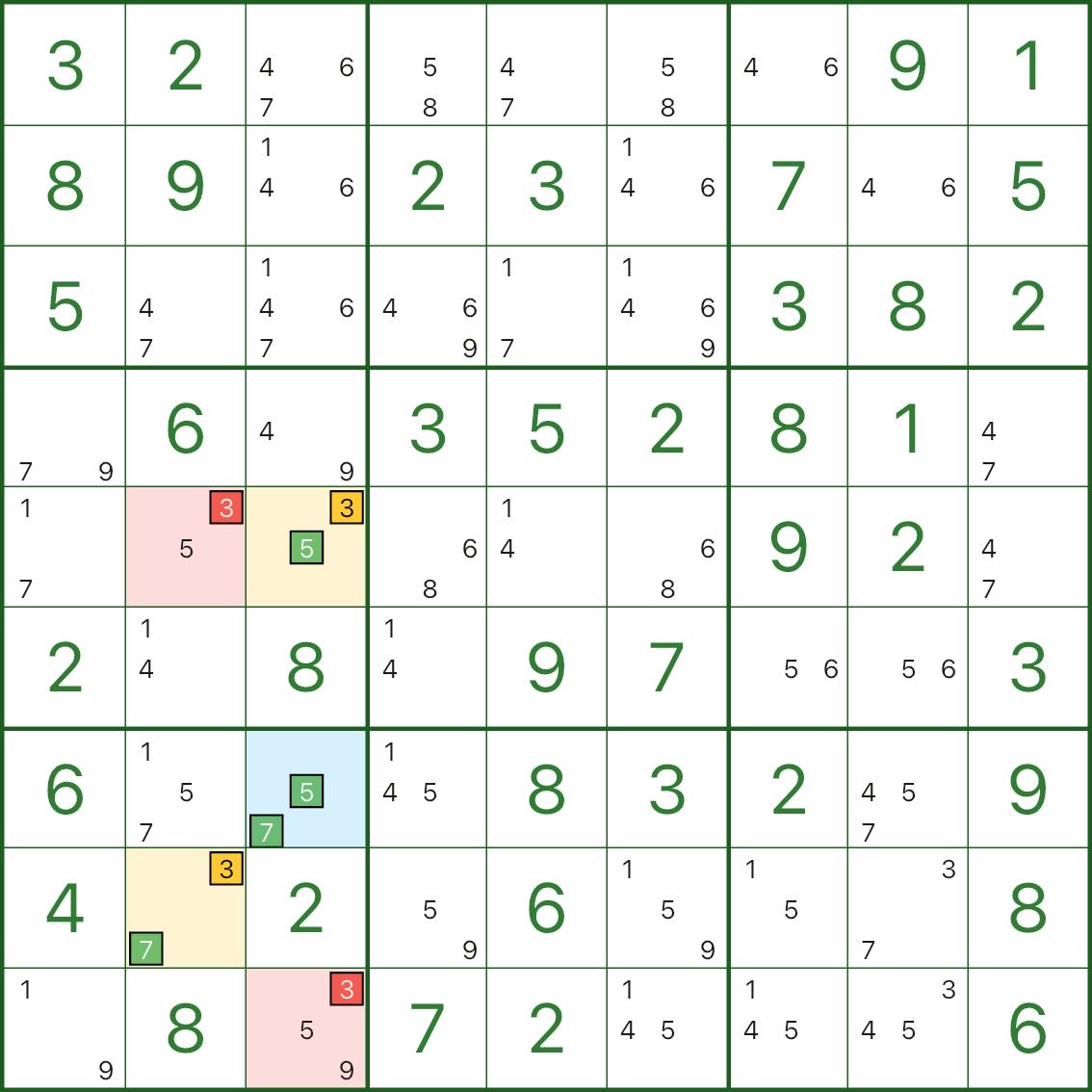
Comment trouver XY-Wing

Liste de contrôle en une ligne : trouver un pivot à deux candidats {x,y}, trouver deux ailes à deux candidats {x,z} et {y,z}, puis éliminer z de toute cellule qui voit les deux ailes.

Dans un vrai casse-tête :

1. Trouvez une cellule avec exactement deux candidats comme pivot (bleu)
2. Trouvez deux cellules capables de voir le pivot, chacune avec exactement deux candidats, en forme de {x,z} et {y,z} (jaune)
3. Toute cellule qui peut voir les deux ailes est un point d'élimination typique : supprimez le candidat z ici (rouge)