Chaîne X

Prérequis : Chain basics

---

1. Aperçu

X-Chain est une technique de chaîne qui se concentre sur un chiffre d.

Pensez-y comme : connectez les positions candidates du même chiffre d en utilisant des liens forts et des liens faibles, pour former un chemin de raisonnement « si… alors… ».

Son utilisation la plus courante est l’élimination :

• les deux points finaux sont le même chiffre d
• si un candidat d peut voir les deux points de terminaison
  ⇒ que le candidat d peut souvent être éliminé

---

2. Procédure pas à pas

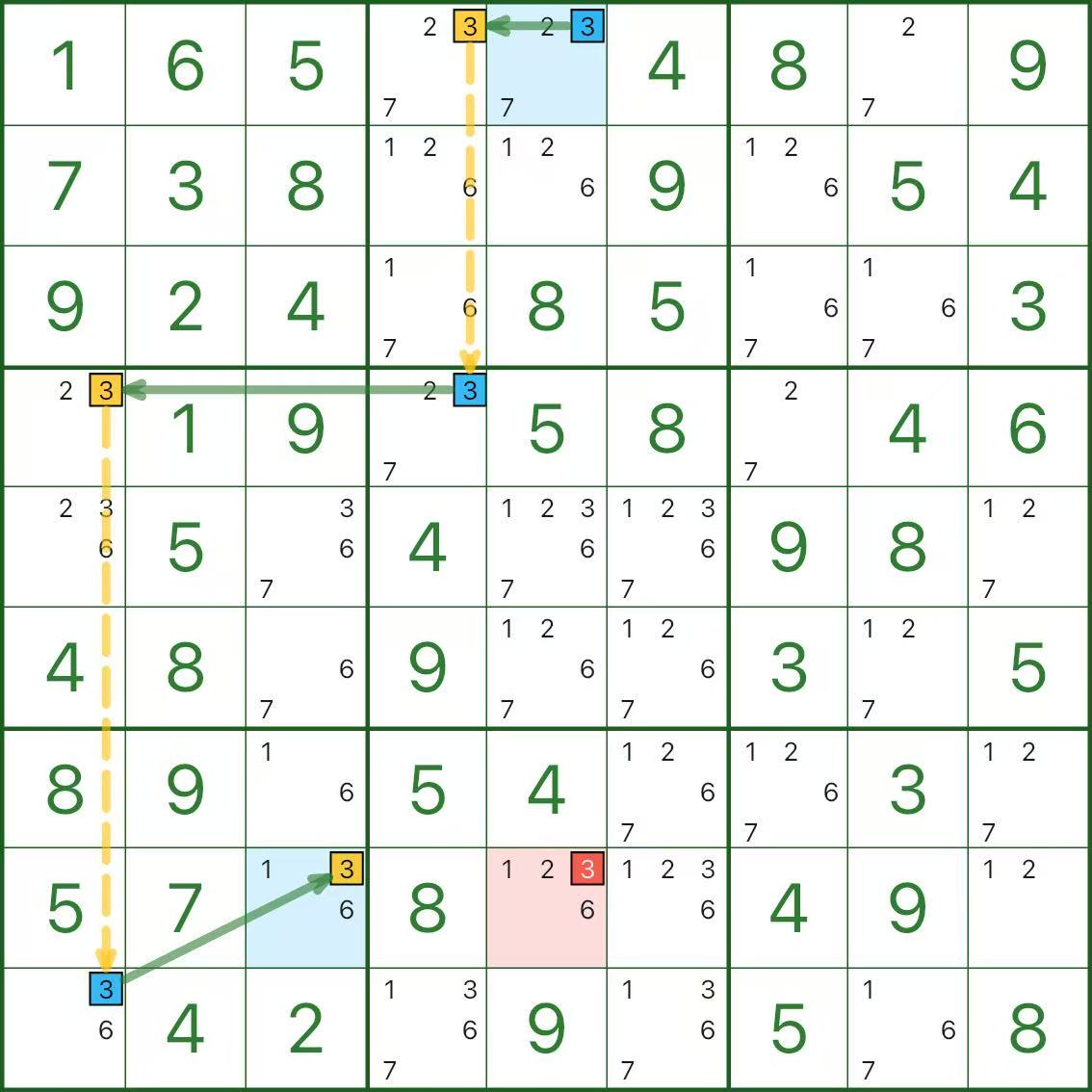
Dans l'image, on parle uniquement du chiffre candidat 3.

À partir du point final bleu r1c5, la chaîne alterne des maillons forts/faibles et atteint finalement l'autre point final bleu r8c3.
Le candidat rouge 3 dans r8c5 est ce que nous voulons éliminer.

Pourquoi pouvons-nous supprimer 3 dans r8c5 ? Une courte contradiction suffit :

1. Supposons que le candidat rouge r8c5 = 3 soit vrai
2. Puis dans la même colonne, r1c5 ne peut pas valoir 3 (le début devient « faux »)
3. Parce que la chaîne alterne maillons forts/faibles :
   • « faux » passe par un lien fort pour forcer « vrai »
   • "vrai" passe par un maillon faible pour forcer "faux"
     pas à pas, la chaîne finit par forcer r8c3 = 3 (la fin devient « vraie »)
4. Mais r8c3 et r8c5 sont sur la même rangée : ils ne peuvent pas être tous les deux 3 — contradiction

L'hypothèse est donc impossible : 3 dans r8c5 peut être éliminé.

---

3. Exemples

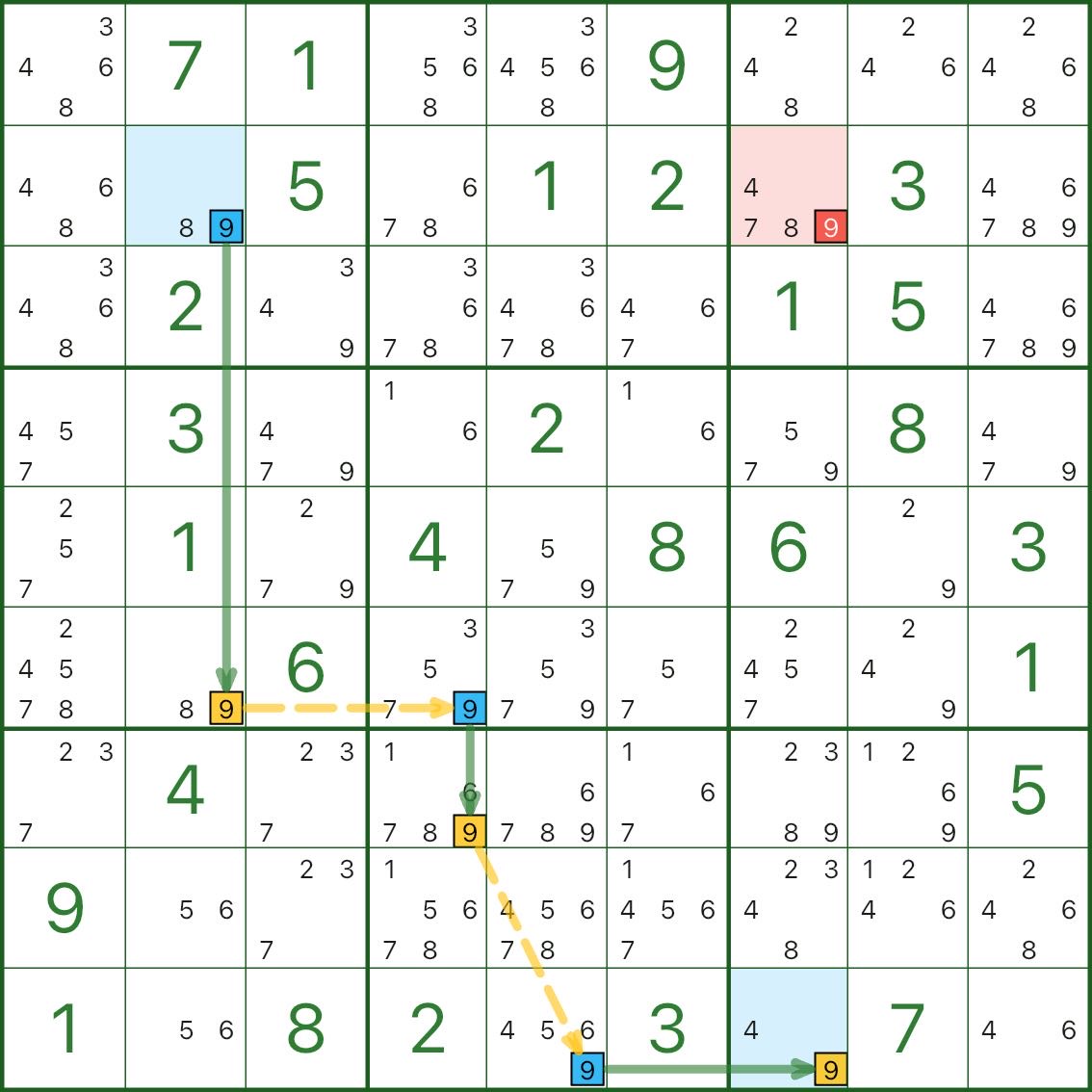
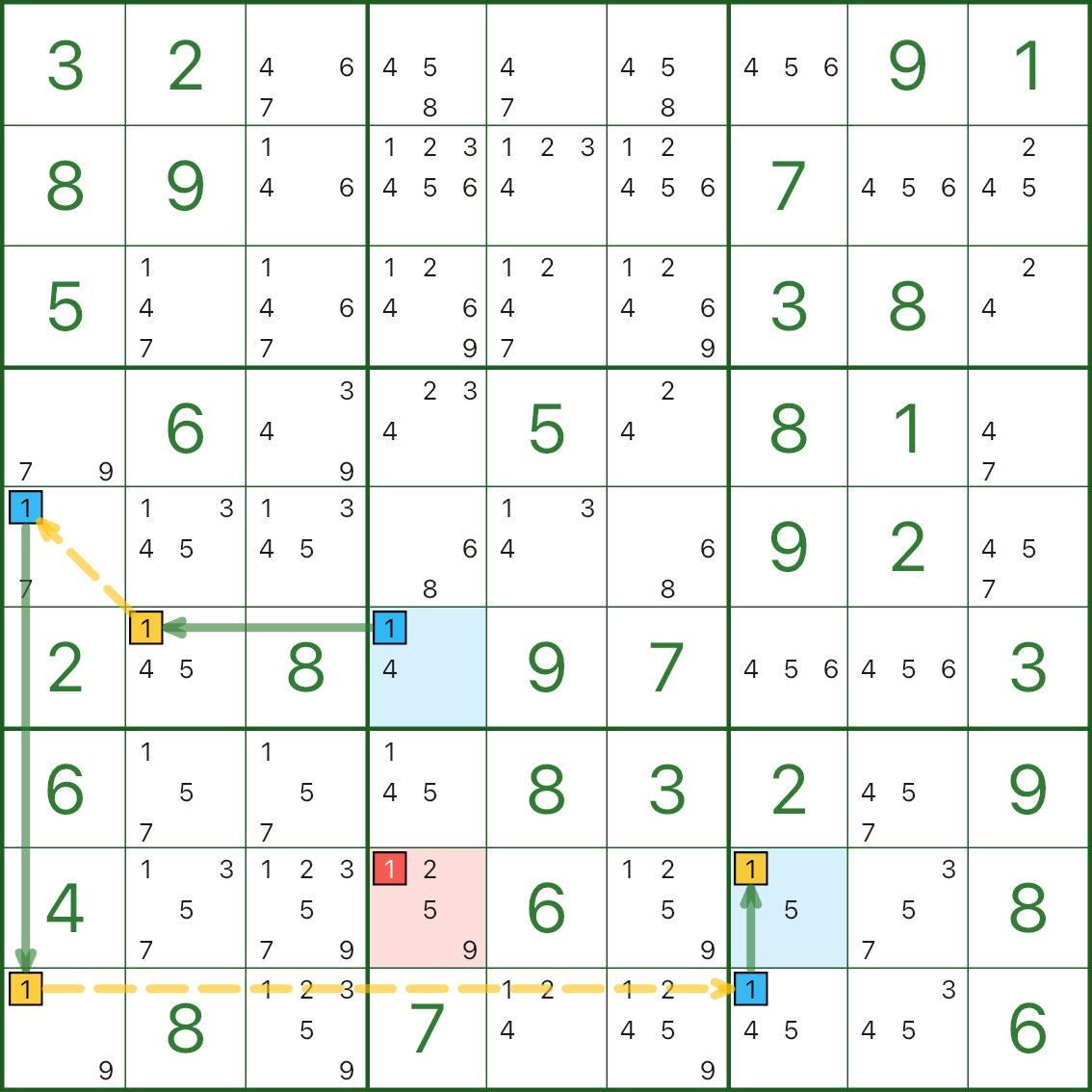
Voici deux autres exemples de X-Chain. Vous n’avez pas besoin de vérifier chaque étape au début – entraînez votre « œil de modèle » :

• se concentrer sur un chiffre d
• trouver une chaîne alternée forte/faible reliant deux extrémités
• trouver un candidat rouge d qui peut voir les deux points de terminaison

---

4. Comment repérer X-Chain

En une phrase : choisissez un chiffre d, construisez une chaîne alternée en utilisant des paires conjuguées (liens forts), puis éliminez d de toute cellule pouvant voir les deux extrémités.

Liste de contrôle pratique :

1. Choisissez un chiffre d (par exemple 3)
2. Dans les lignes/colonnes/cases, recherchez les endroits où d a exactement deux postes candidats (c'est un lien fort)
3. Relier ces segments en utilisant des relations de type « pouvoir se voir » (maillons faibles) pour former une chaîne alternée
4. Trouvez un candidat d qui peut voir les deux points de terminaison — c'est une élimination typique