Rectangle unique (UR)

Prérequis : UR s'appuie sur le fait que le puzzle a exactement une solution.
Si vous ne l'avez pas encore lu, commencez ici :
Uniqueness

---

1. Aperçu

Unique Rectangle (UR) est une famille de techniques qui utilisent la propriété single-solution pour éliminer des candidats (et parfois placer un numéro).

Il se concentre sur une « forme dangereuse » :

• quatre cellules forment un rectangle 2×2 (deux lignes × deux colonnes, s'étendant exactement sur deux cases)
• les quatre coins contiennent les deux mêmes candidats principaux (par exemple, 1 et 7)

Si nous laissons ces quatre cellules avec uniquement cette paire, le rectangle peut souvent être rempli de deux manières différentes (en échangeant les deux chiffres), ce qui briserait l'unicité.
Ainsi, sous l'hypothèse d'unicité, nous pouvons conclure : certains candidats doivent être supprimés, ou une cellule doit prendre une valeur spécifique.

---

2. Procédure pas à pas (5 types)

Les 5 images ci-dessous correspondent aux 5 types d'UR courants (les astuces dans l'application les qualifient de type I à V).

Guide des couleurs :

• Cellules bleues : le rectangle UR (la structure de base)
• Notes jaunes : candidats sur lesquels nous nous concentrons dans le raisonnement
• Marques rouges : candidats à éliminer / ou une cellule paramétrable

Type I : toit simple → une valeur forcée

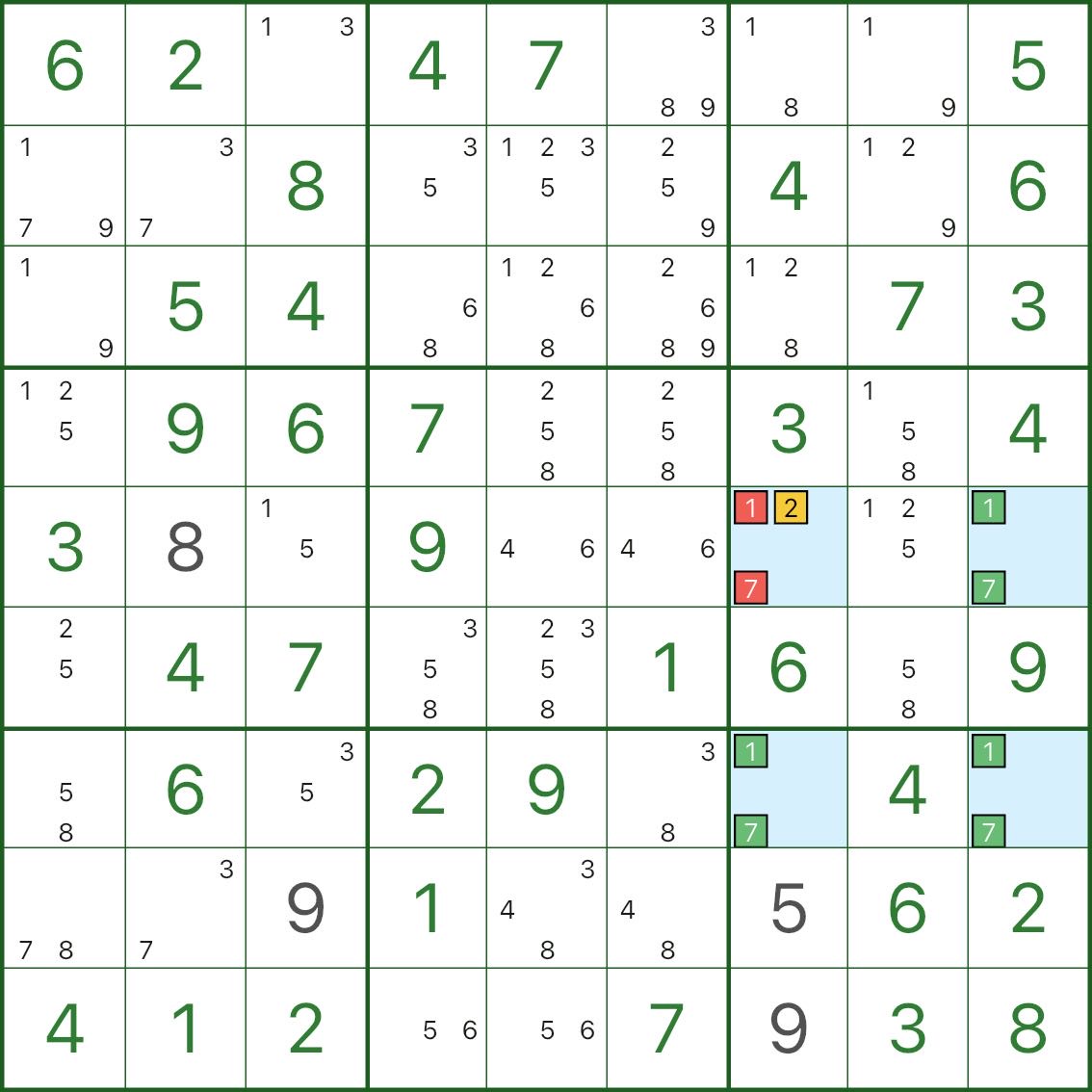
Regardez les quatre cellules bleues : elles forment un rectangle et contiennent toutes les candidats 1 et 7.
La cellule r5c7 a également un candidat supplémentaire 2.

Si 2 n'est pas vrai dans r5c7, alors r5c7 n'aurait que 1 et 7.
Cela rendrait les quatre coins « {1,7} uniquement », permettant deux remplissages échangeables (rompant l'unicité).

Donc sous unicité :

• r5c7 ne peut pas garder les candidats 1 et 7
• donc r5c7 doit être 2

---

Type II : deux toits → éliminer c qui voit les deux toits

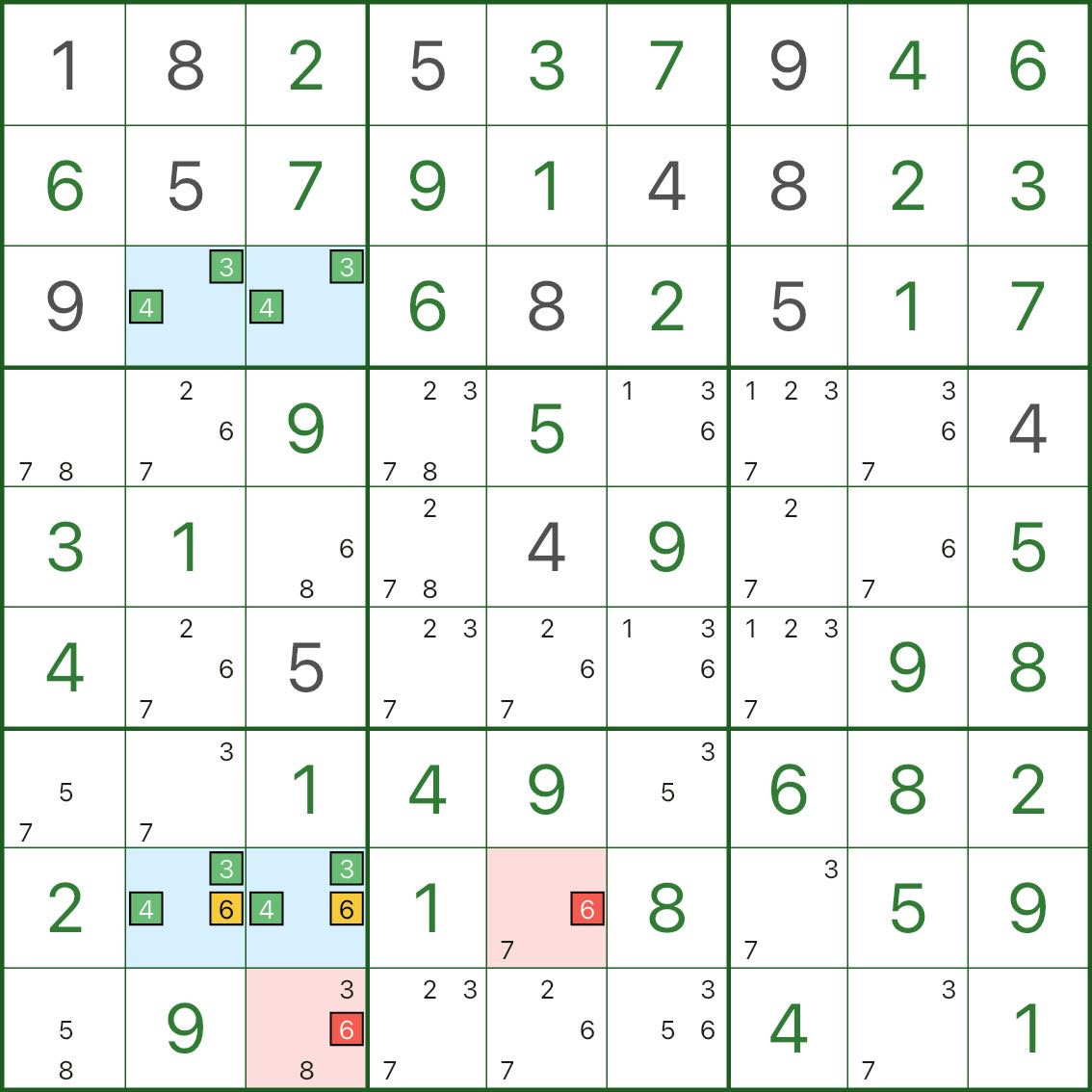
Ici, le rectangle bleu est basé sur les candidats principaux 3 et 4.
Deux cellules bleues r8c2 et r8c3 contiennent également le candidat 6 (il s'agit donc de {3,4,6}).

Considérons maintenant un candidat rouge 6 (par exemple dans r8c5 ou r9c3) qui peut voir les deux cellules de toit :

• si ce 6 rouge était vrai, les deux toits seraient forcés pas 6
• les toits s'effondreraient jusqu'à {3,4} seulement
• le rectangle redevient un motif {3,4} mortel (rompant l'unicité)

Ces candidats rouges 6 ne peuvent donc pas être vrais et peuvent être éliminés.

---

Type III : traiter les toitures comme un « package » et former un sous-ensemble

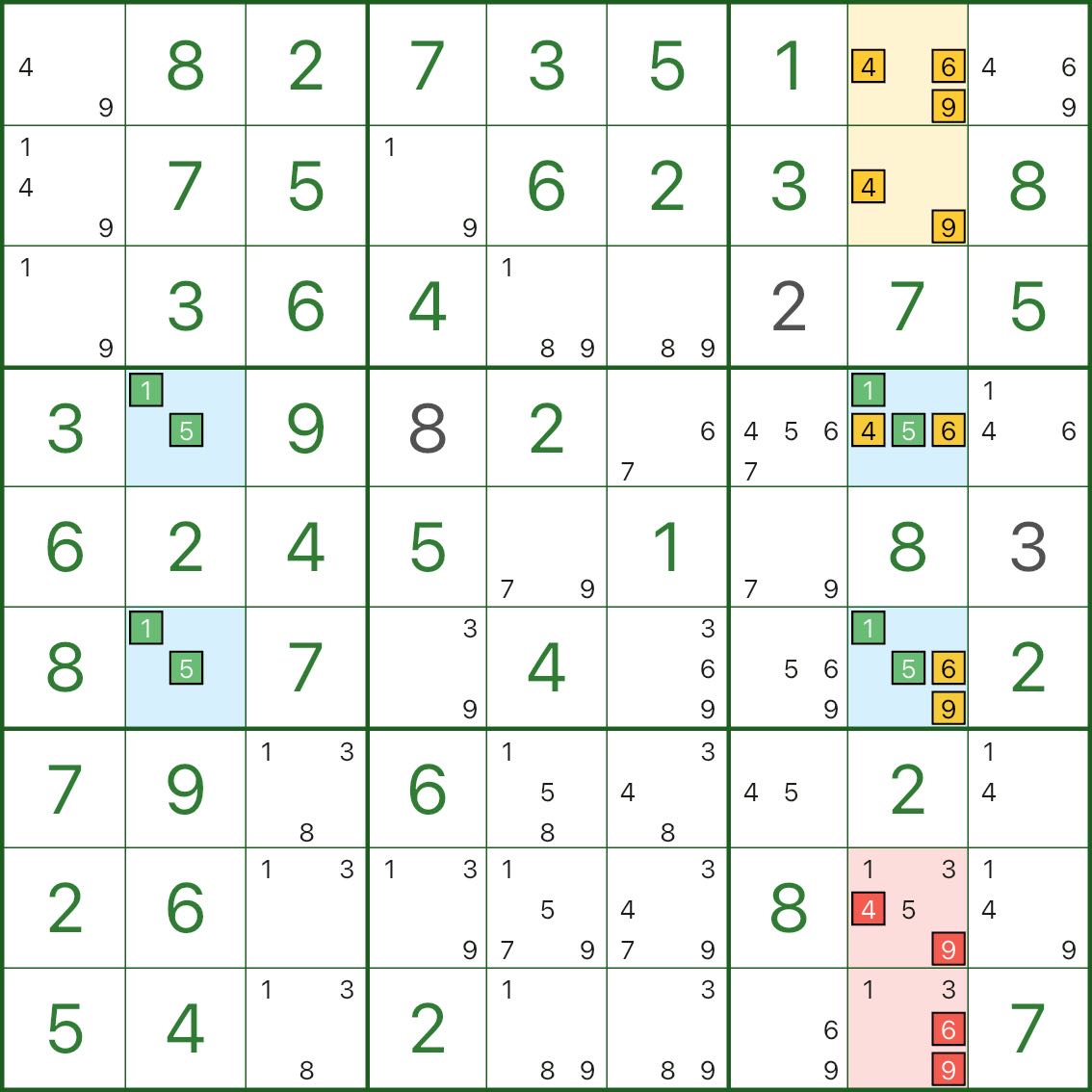
Celui-ci se concentre sur la colonne 8 :

• deux cellules bleues dans la colonne 8 contiennent toutes deux les candidats principaux 1 et 5
• ils partagent également des chiffres supplémentaires 4, 6, 9 (chacun vaut donc {1,5,4,6,9})

L’unicité impose une contrainte importante :

• parmi ces deux cellules bleues, au moins une doit prendre un chiffre de {4,6,9}
• sinon les deux ne s'appuieraient que sur {1,5}, transformant le rectangle en un motif mortel

Nous pouvons donc traiter « les chiffres supplémentaires {4,6,9} des deux cellules bleues » comme un package.
Avec les cellules jaunes r1c8 et r2c8, cela verrouille efficacement les chiffres 4, 6, 9 dans un petit sous-ensemble de la colonne 8.

Par conséquent, tous les autres candidats 4/6/9 de la colonne 8 (marqués en rouge) peuvent être éliminés.

---

Type IV : une paire conjuguée force un chiffre → élimine l'autre

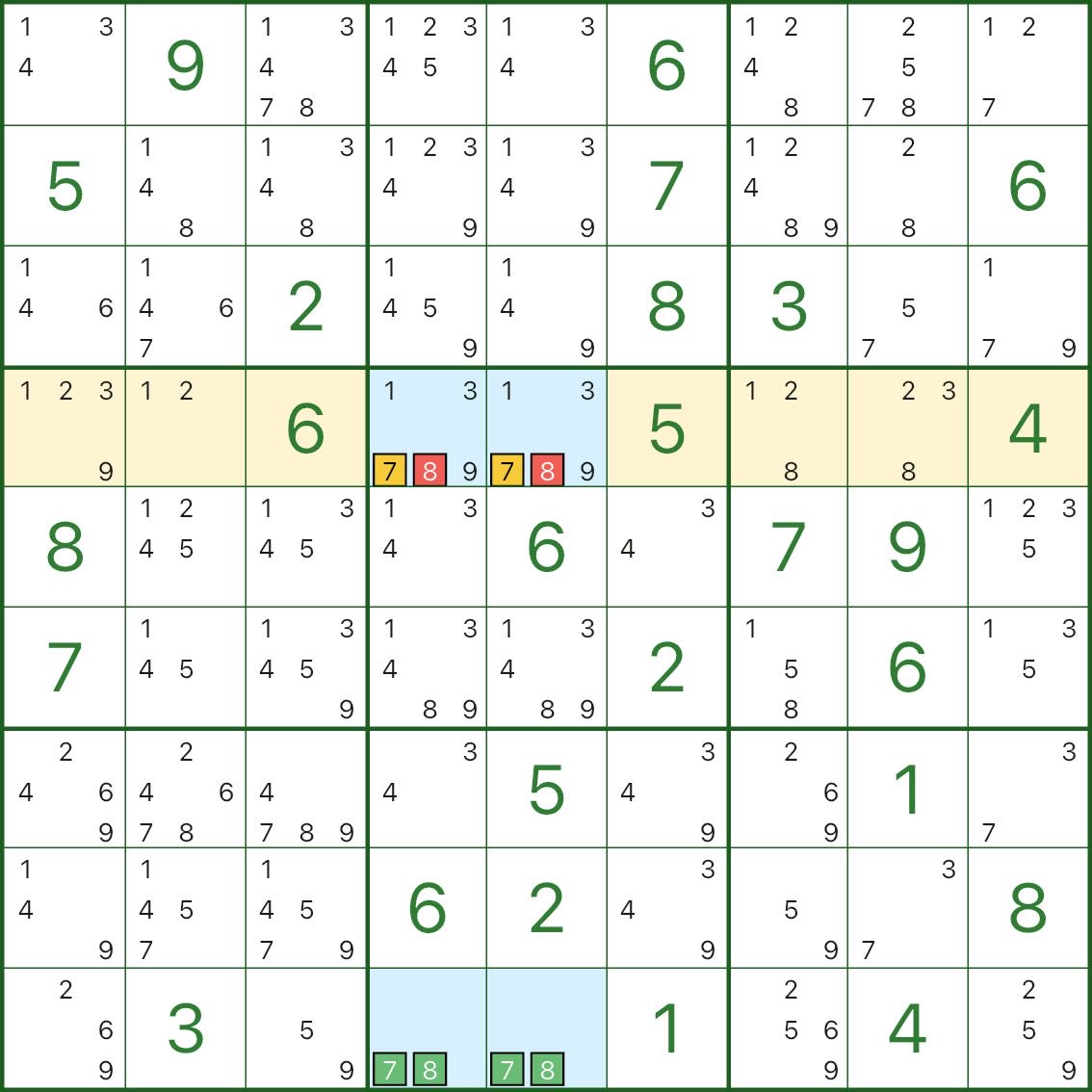
Le rectangle bleu est à nouveau construit sur une paire de cœurs (ici 7 et 8).Dans la ligne 4, le candidat 7 apparaît uniquement dans les deux cellules bleues r4c4 et r4c5.
Cela signifie :

• l'un des r4c4 / r4c5 doit être 7

Avec cette contrainte, garder le candidat 8 dans ces mêmes cellules bleues permettrait toujours au rectangle de s'effondrer en une structure mortelle (rompant l'unicité).

Nous pouvons donc éliminer 8 de r4c4 et r4c5.

---

Type V : toits multiples (2 ou 3) → éliminer c qui voit toutes les cellules du toit

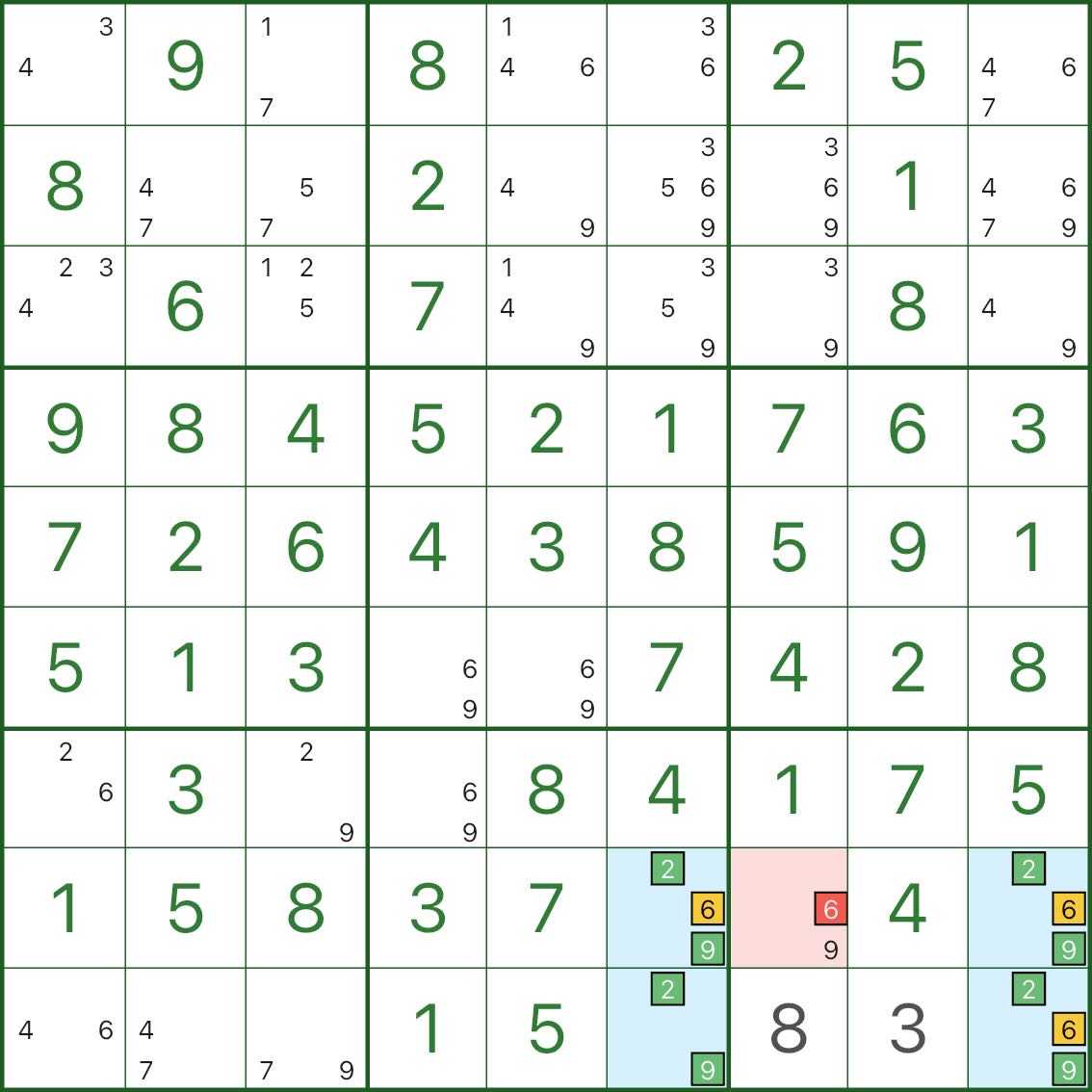
Le type V n’est pas strictement « trois toits ». L'idée clé est la suivante :

• il y a 2 ou 3 cellules de toit dans le rectangle, et elles partagent toutes le même candidat supplémentaire c
• s'il n'y a que 2 cellules de toit, elles ne partagent généralement pas la même ligne/colonne/boîte (si c'est le cas, c'est plus proche du type II)
• si le candidat c d'une cellule peut voir toutes ces cellules du toit, alors ce c ne peut pas être vrai et peut être éliminé

Dans cette image, le rectangle bleu comporte principalement les chiffres 2, 6, 9 :

• trois coins bleus sont {2,6,9}
• le coin bleu restant est {2,9} (manque 6)

Regardez maintenant la cellule rouge r8c7 : elle a le candidat 6 et elle peut voir toutes les {2,6,9} cellules du toit dans ce modèle.

Si r8c7 = 6 :

• les trois cellules du toit seraient forcées non-6
• ils s'effondreraient en {2,9} seulement
• le rectangle devient un motif {2,9} mortel (rompant l'unicité)

Ainsi le candidat 6 dans r8c7 ne peut pas être vrai et peut être éliminé.

---

3. Exemples

Les images 1 à 5 de cet article sont déjà des exemples pour les types I à V.
Lorsque vous vous entraînez, essayez d’abord de repérer le rectangle bleu, puis faites correspondre les marques jaunes/rouges au raisonnement ci-dessus.

---

4. Comment repérer un rectangle unique

Dans les vrais puzzles, vous pouvez rechercher dans cet ordre :

1. Recherchez quatre cellules vides qui forment un rectangle 2 × 2 (deux lignes × deux colonnes) et s'étendent sur exactement deux cases
2. Vérifiez si les quatre coins partagent les deux mêmes candidats principaux (la « paire mortelle »)
3. Classez ensuite selon l'apparence des candidats supplémentaires :
   • un seul coin a des candidats supplémentaires → Type I (souvent une valeur forcée)
   • deux coins partagent le même chiffre supplémentaire c → Type II
   • les chiffres supplémentaires des toits peuvent former un sous-ensemble dans une ligne/colonne/boîte → Type III
   • dans une maison, un chiffre central n'apparaît que dans deux cellules rectangulaires → Type IV
   • deux ou trois coins partagent le même chiffre supplémentaire c (pour 2 toits, ils ne partagent généralement pas une maison) → Type V

C'est UR en une phrase : ne laissez jamais le rectangle s'effondrer en un motif mortel, sinon l'unicité serait brisée.