Paires et sous-ensembles

Paires et sous-ensembles nus/cachés

Les paires et les sous-ensembles font partie des techniques d’« élimination de candidats » les plus utiles. Ils portent des noms différents, mais ils font tous la même chose :

Dans une maison (une ligne/colonne/boîte), un petit ensemble de cellules et un petit ensemble de chiffres « se réservent les emplacements » les uns pour les autres — afin que ces chiffres ne puissent pas apparaître ailleurs dans cette maison.

Vous n’avez pas besoin de mémoriser le jargon. Une règle simple :

• Naked : partez de ce que montrent les cellules (ces cellules contiennent uniquement ces chiffres)
• Caché : commencez à partir de l'endroit où un chiffre peut aller (ces chiffres ne peuvent aller que dans ces cellules)

---

1. Paire nue

Dans la même maison, si deux cellules contiennent toutes deux seulement les deux mêmes candidats (par exemple {a,b}), vous avez une paire nue.

Cela signifie :

• Une cellule doit être a, l'autre doit être b (ordre inconnu)
• Ainsi, les candidats a et b peuvent être supprimés de toutes les autres cellules vides de cette maison

Tout d'abord, regardez l'image ci-dessous : concentrez-vous sur la case 3 en surbrillance et les deux cellules vertes r2c9 et r3c9.
Vous remarquerez qu'ils ne peuvent être que {1,5}.

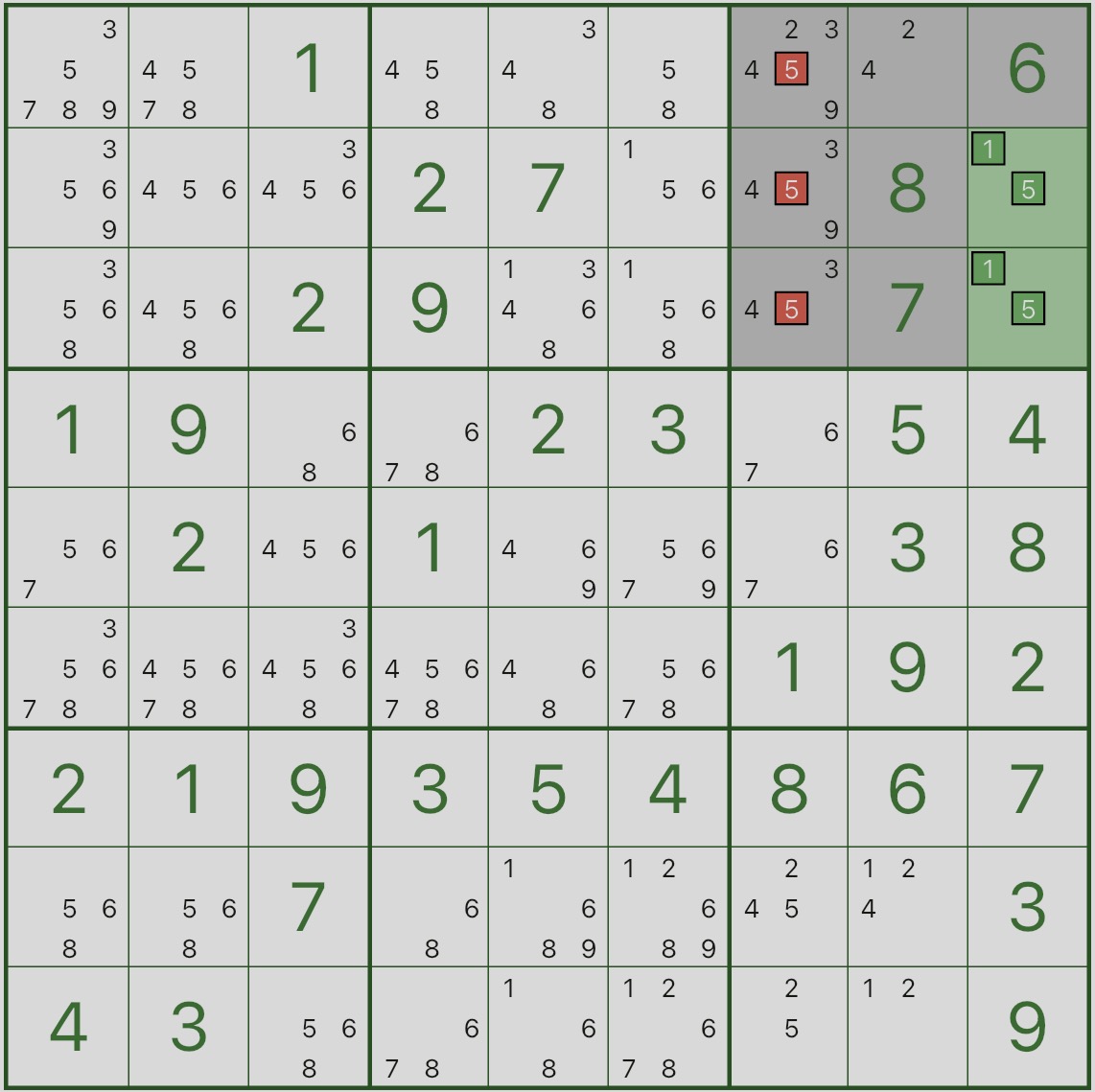
Cela signifie : dans la case 3, les chiffres 1 et 5 sont « réservés » pour r2c9 et r3c9.

Regardez maintenant les candidats rouges : le candidat 5 dans r1c7, r2c7, r3c7 peut être supprimé.

Une preuve rapide par contradiction :

• Supposons que r1c7 vaut 5 (la même logique s'applique à r2c7 et r3c7)
• Alors la case 3 contient déjà un 5, donc r2c9 et r3c9 ne peuvent pas être 5 et sont forcés d'être 1
• Mais r2c9 et r3c9 partagent la même colonne (colonne 9), donc ils ne peuvent pas tous les deux être 1 — contradiction
  ⇒ ces candidats rouges 5 sont impossibles et peuvent être supprimés

---

2. Paire cachée

Dans la même maison, si le candidat a apparaît dans exactement deux cellules et que le candidat b apparaît également dans les mêmes deux cellules, vous avez une paire cachée.

Ces deux cellules peuvent afficher des candidats supplémentaires, mais a et b y sont déjà verrouillés, vous pouvez donc :

• Supprimez tous les candidats sauf a et b de ces deux cellules

Tout d’abord, regardez l’image ci-dessous : concentrez-vous sur la colonne 4 en surbrillance.
Recherchez où les candidats 4 et 5 apparaissent dans cette colonne : vous verrez qu'ils apparaissent uniquement dans r1c4 et r6c4.

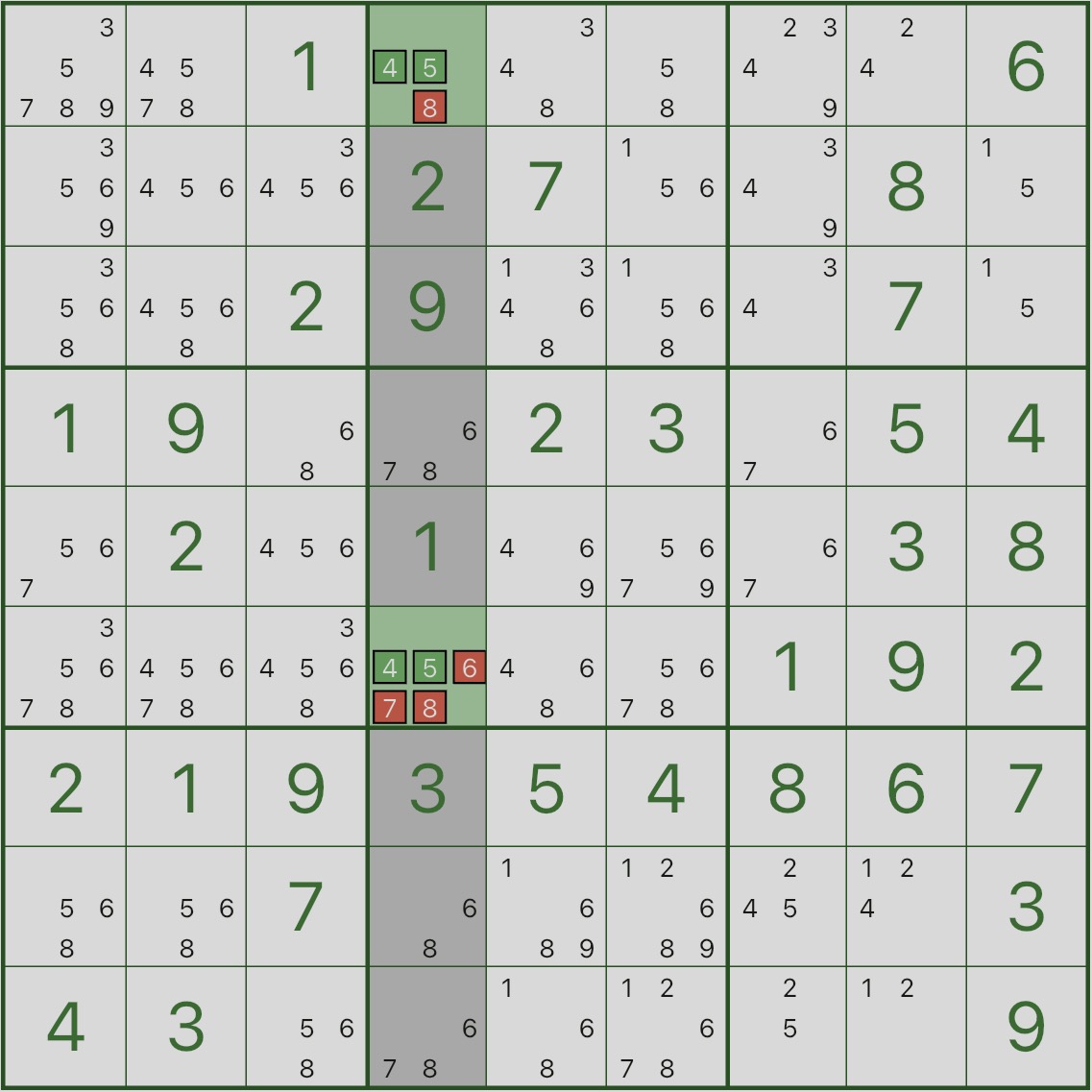
Cela signifie : dans la colonne 4, les chiffres 4 et 5 doivent être placés entre r1c4 et r6c4.

Pourquoi pouvons-nous supprimer d’autres candidats de r1c4 et r6c4 ?

• Supposons que r1c4 prenne un chiffre qui n'est pas 4 ou 5
• Ensuite, 4 et 5 devraient entrer dans r6c4 uniquement
• Une seule cellule ne peut pas contenir à la fois 4 et 5 — contradiction
  ⇒ r1c4 et r6c4 doivent être {4,5}, donc les autres candidats dans ces cellules peuvent être supprimés

---

3. Sous-ensemble nu (Triple / Quad)

C’est l’idée du « couple nu », généralisée :

Si N cellules dans une maison ne contiennent collectivement que N chiffres (par exemple, trois cellules ne contiennent que {a,b,c}), vous avez un triple nu. La même idée s'applique aux quads.

Ces chiffres doivent être placés dans ces N cellules, donc :

• Supprimez ces chiffres (par exemple a, b, c) de toutes les autres cellules vides de cette maison

Tout d'abord, regardez l'image ci-dessous : concentrez-vous sur la ligne 8 en surbrillance et les trois cellules r8c1, r8c2, r8c4.
Vous remarquerez que ces trois cellules ne contiennent collectivement que {5,6,8}.

Cela signifie : dans la ligne 8, les chiffres 5, 6, 8 doivent être placés entre r8c1, r8c2, r8c4.

C’est pourquoi les candidats rouges 5, 6, 8 dans le reste de la rangée 8 peuvent être supprimés.

Une simple vision contradictoire :

• Si une autre cellule de la ligne 8 "prend" un des {5,6,8}
• Ensuite, ces trois cellules devraient être remplies en utilisant seulement deux chiffres pour trois cellules
• Ça ne peut pas marcher — contradiction

---

4. Sous-ensemble caché (Triple / Quad)

C’est l’idée de « paire cachée », généralisée :

Si les N chiffres d'une maison n'apparaissent que dans les mêmes N cellules (même si ces cellules contiennent des candidats supplémentaires), vous avez un triple/quad caché.

Ces N chiffres sont verrouillés sur ces N cellules, donc :

• Supprimez tous les candidats sauf ces N chiffres de ces cellules

Tout d’abord, regardez l’image ci-dessous : concentrez-vous sur la colonne 5 en surbrillance.
Vous remarquerez que les chiffres 4,7,8 apparaissent uniquement dans r1c5, r8c5, r9c5.

Cela signifie : dans la colonne 5, les chiffres 4, 7, 8 doivent être placés entre r1c5, r8c5, r9c5.

Par conséquent, dans ces trois cellules, nous pouvons supprimer tout autre candidat autre que 4, 7 ou 8.

Pourquoi est-ce sûr ?

• Si l'une de ces cellules prenait un chiffre différent
• Alors 4, 7 et 8 auraient moins de trois emplacements à insérer — contradiction

---

5. Astuces pour les repérer plus rapidement

• Gardez les candidats raisonnablement complets (vous en aurez besoin pour des énigmes plus difficiles)
• Recherchez d'abord les modèles nus : commencez par des cellules avec très peu de candidats (2, 3 ou 4)
• Recherchez ensuite des motifs cachés : dans une maison, vérifiez si un chiffre est limité à 2, 3 ou 4 points
• Après les éliminations, faites une pause et regardez à nouveau : les candidats simplifiés révèlent souvent l'étape suivante