Cerf-volant

Prérequis : Chain Basics

Description

Le cerf-volant est une technique d'élimination des candidats à un chiffre : concentrez-vous sur un chiffre d.

Vous trouvez deux candidats pour d dans une ligne et deux candidats pour d dans une colonne, avec une paire « à égalité » en étant dans la même case.
Ensuite, tout candidat d qui peut voir les deux points finaux peut être éliminé.

---

Explication

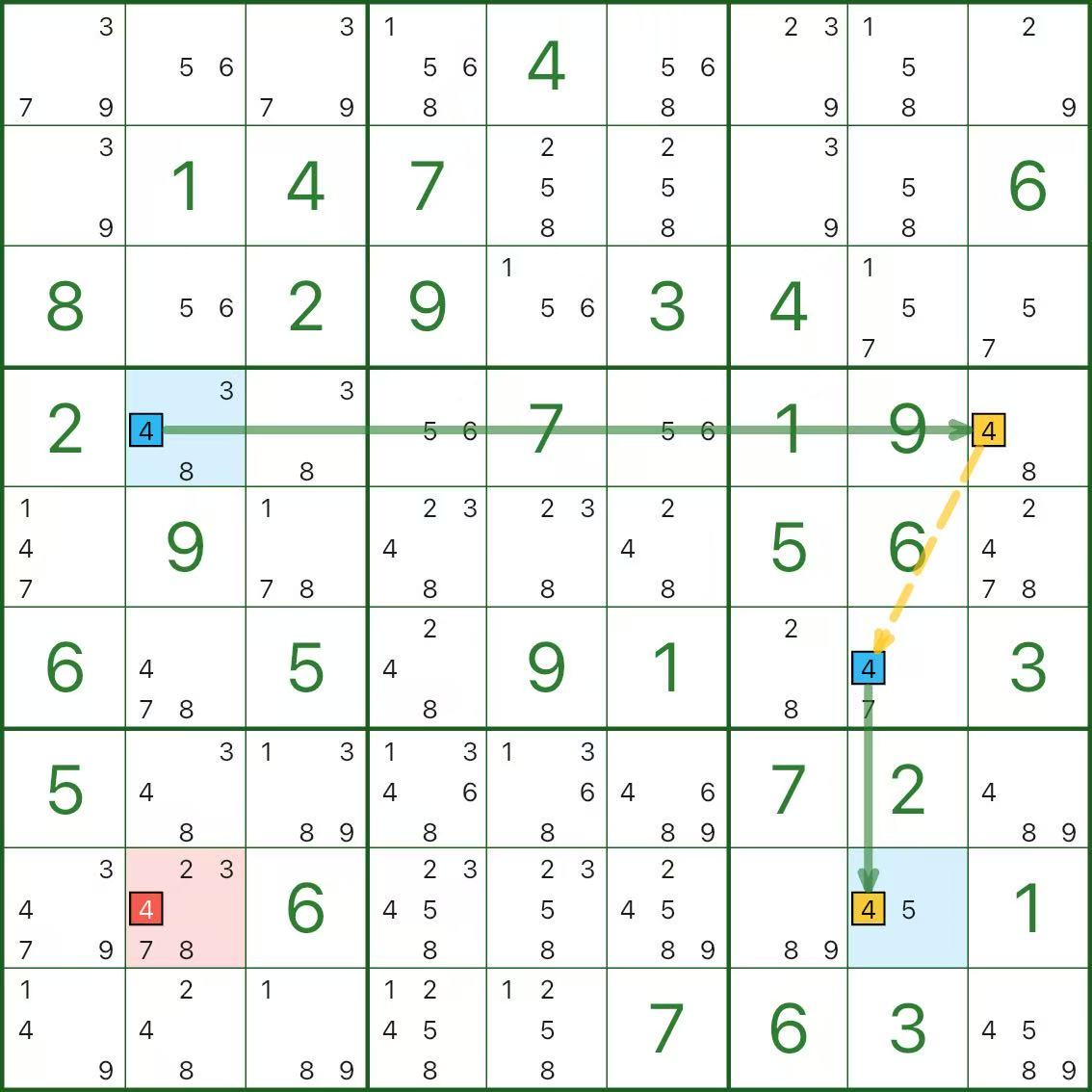
Dans l'image ci-dessus, le chiffre cible est 4.
La chaîne est r4c2 → r4c9 → r6c8 → r8c8. Le candidat rouge est le chiffre 4 dans r8c2 et les deux points finaux (r4c2, r8c8) sont surlignés en bleu.

Pourquoi peut-on l'éliminer ? Une courte contradiction suffit :

• Supposons r8c2 = 4 (le candidat rouge est vrai)
• r8c2 peut voir les deux points de terminaison, donc r4c2 ≠ 4 et r8c8 ≠ 4
• Deux liens forts sont obligés de « remplir » 4 : sur la ligne 4, r4c9 = 4 ; sur la colonne 8, r6c8 = 4
• Mais r4c9 et r6c8 sont dans la même case, donc ils ne peuvent pas être tous les deux 4 → contradiction

Par conséquent, r8c2 ne peut pas être 4 et le candidat rouge 4 peut être éliminé.

---

Exemples

Les deux images suivantes sont d'autres exemples de cerfs-volants. Utilisez-les comme références :

---

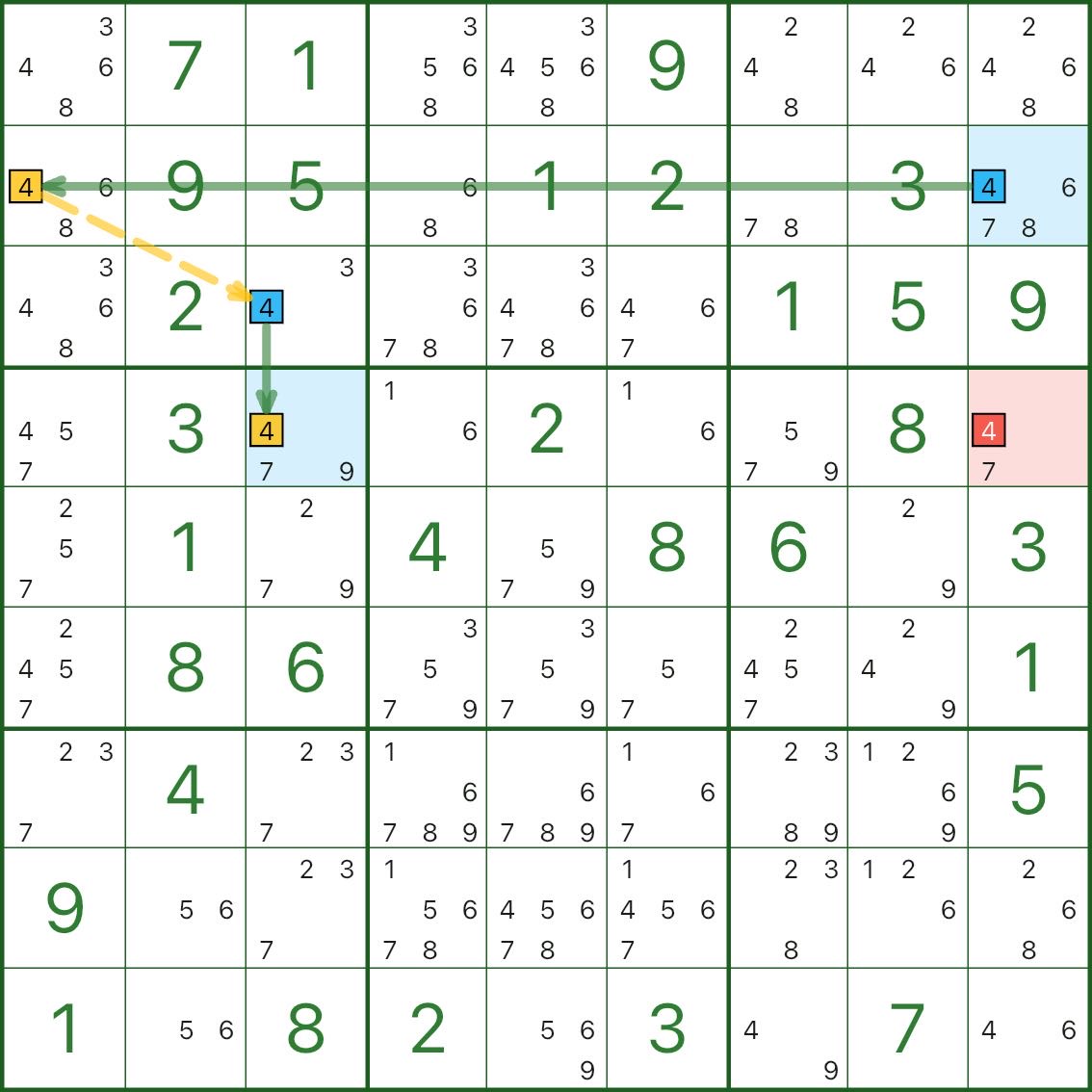
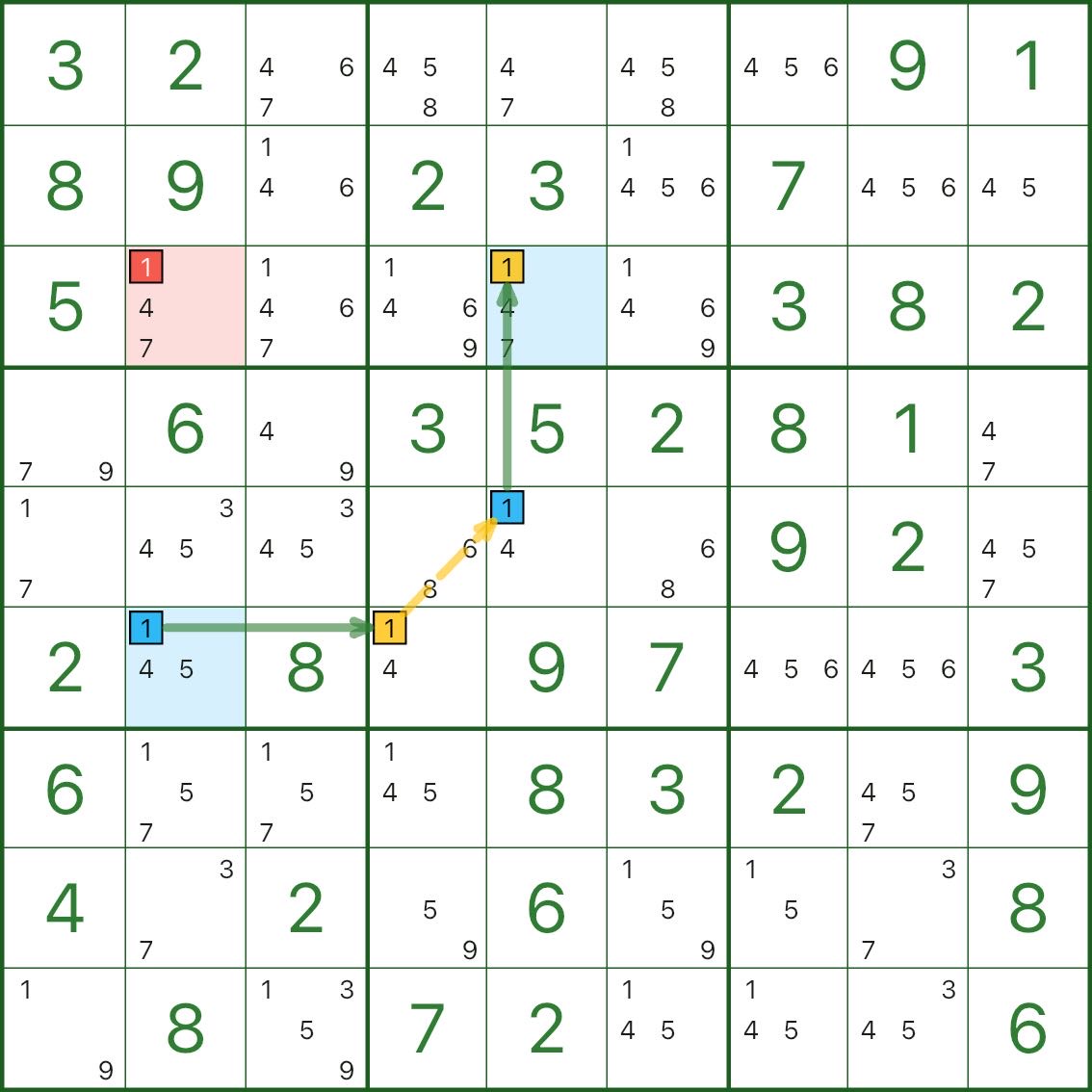
Comment trouver un cerf-volant

Liste de contrôle en une ligne : deux dans une rangée + deux dans une colonne + une égalité de boîte → éliminer l'endroit où les deux points finaux sont vus.

Dans un vrai casse-tête :

1. Choisissez un chiffre d
2. Recherchez une ligne (ou une colonne) où d apparaît dans exactement 2 cellules candidates (un lien fort)
3. Trouvez une colonne (ou une ligne) perpendiculaire où d apparaît également dans exactement 2 cellules candidates (un autre lien fort)
4. Vérifiez qu'un candidat de chaque paire se trouve dans la même case (le « nœud »)
5. Les deux candidats restants sont les points finaux : éliminez d de toute cellule pouvant voir les deux points finaux