Rectangle vide

> Prérequis : [Chain Basics](learning://chains)

Advanced

Rectangle vide

Prérequis : Chain Basics

Description

Le rectangle vide est une technique d'élimination des candidats à un chiffre : concentrez-vous sur un chiffre d.

À l'intérieur d'une boîte, le chiffre d peut former une distribution spéciale en forme de croix/en L — ce qui signifie que tous les candidats d dans cette boîte se trouvent sur une ligne et une colonne.
Si une chaîne courte force d sur ces lignes, vous pouvez parfois arriver à une contradiction très claire : la boîte se retrouve sans place pour d, donc l'hypothèse initiale doit être fausse.

Explication

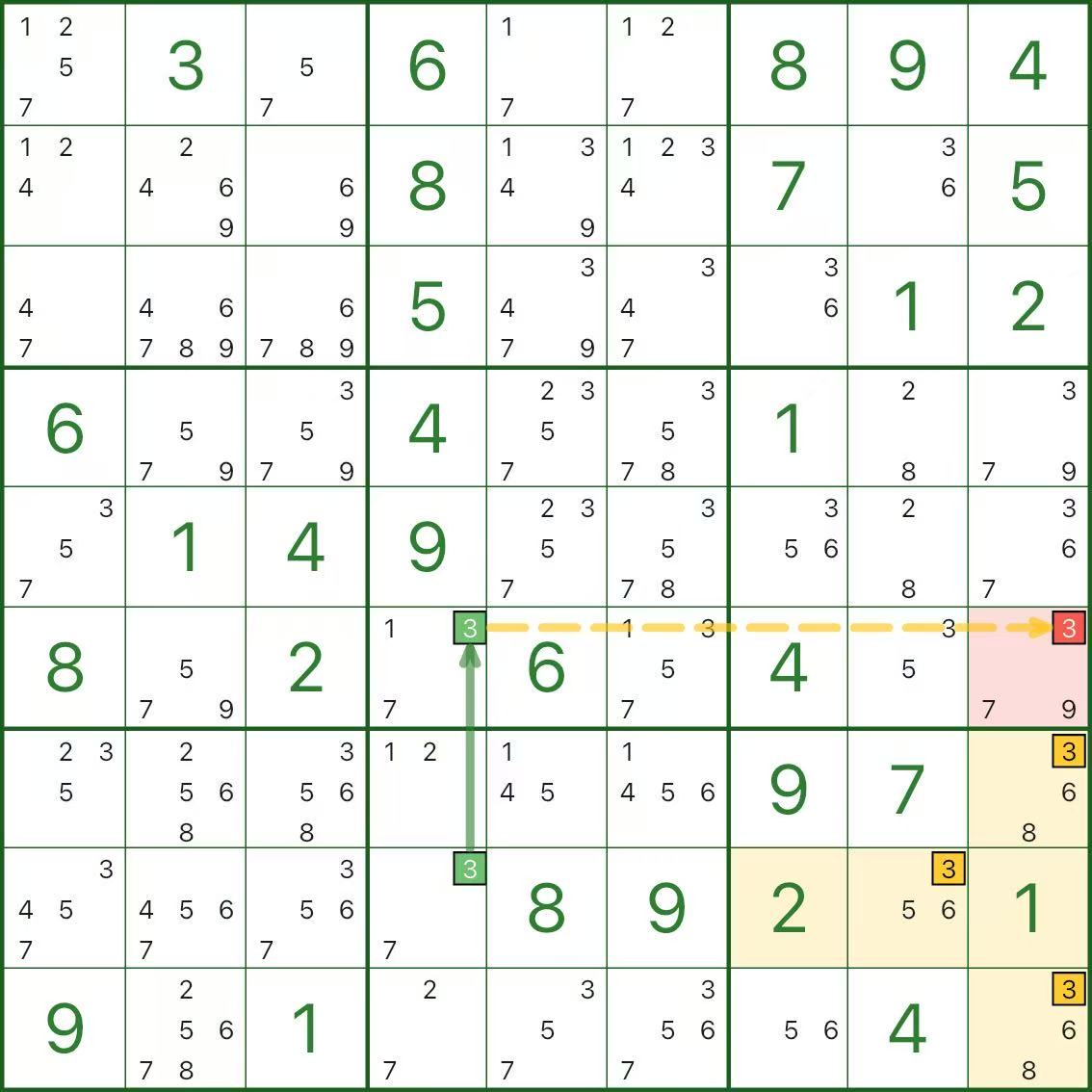
Empty Rectangle walkthrough example

Dans l'image ci-dessus, nous souhaitons éliminer le candidat 3 en r6c9 (rouge).

Voici la courte contradiction :

Supposons r6c9 = 3 (le candidat rouge est vrai)
Une ligne ne peut pas contenir deux 3, donc r6c4 ≠ 3
Dans la colonne 4, le chiffre 3 n'a que deux cellules possibles : r6c4 ou r8c4
Puisque r6c4 n'est pas 3, r8c4 doit être 3
Regardez maintenant la case 9 (la case rectangulaire vide) :
avec r6c9 = 3 (même colonne) et r8c4 = 3 (même ligne), les 3 positions restantes dans la case 9 sont éliminées, donc la case 9 n'a pas de place pour le chiffre 3 (contradiction)

L'hypothèse est donc impossible : r6c9 ne peut pas être 3, et le candidat 3 peut être éliminé.

Exemples

Ces images montrent davantage de motifs de rectangles vides. Utilisez-les comme références pour « boîte croix/forme L + chaîne courte + élimination (rouge) » :

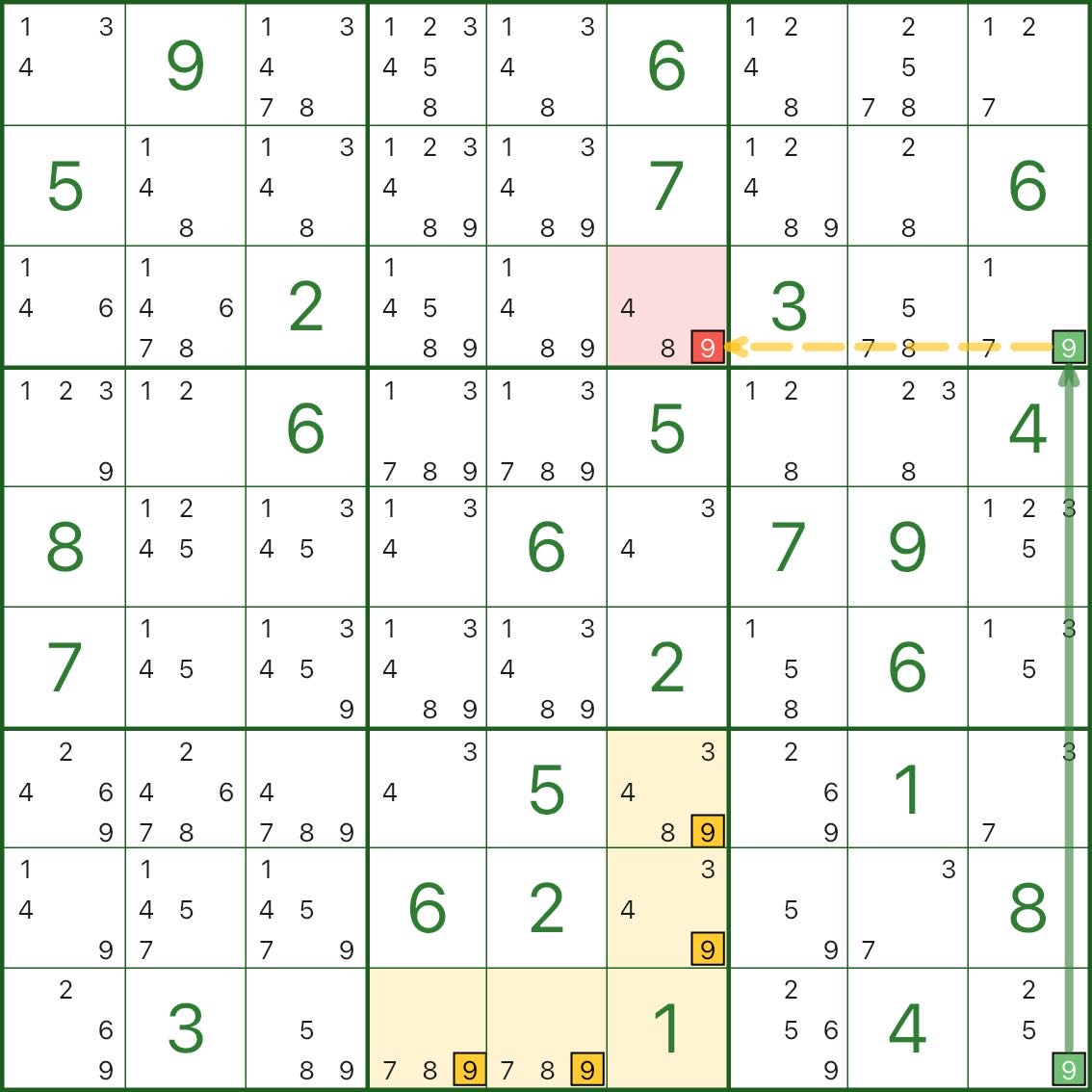
Empty Rectangle example A

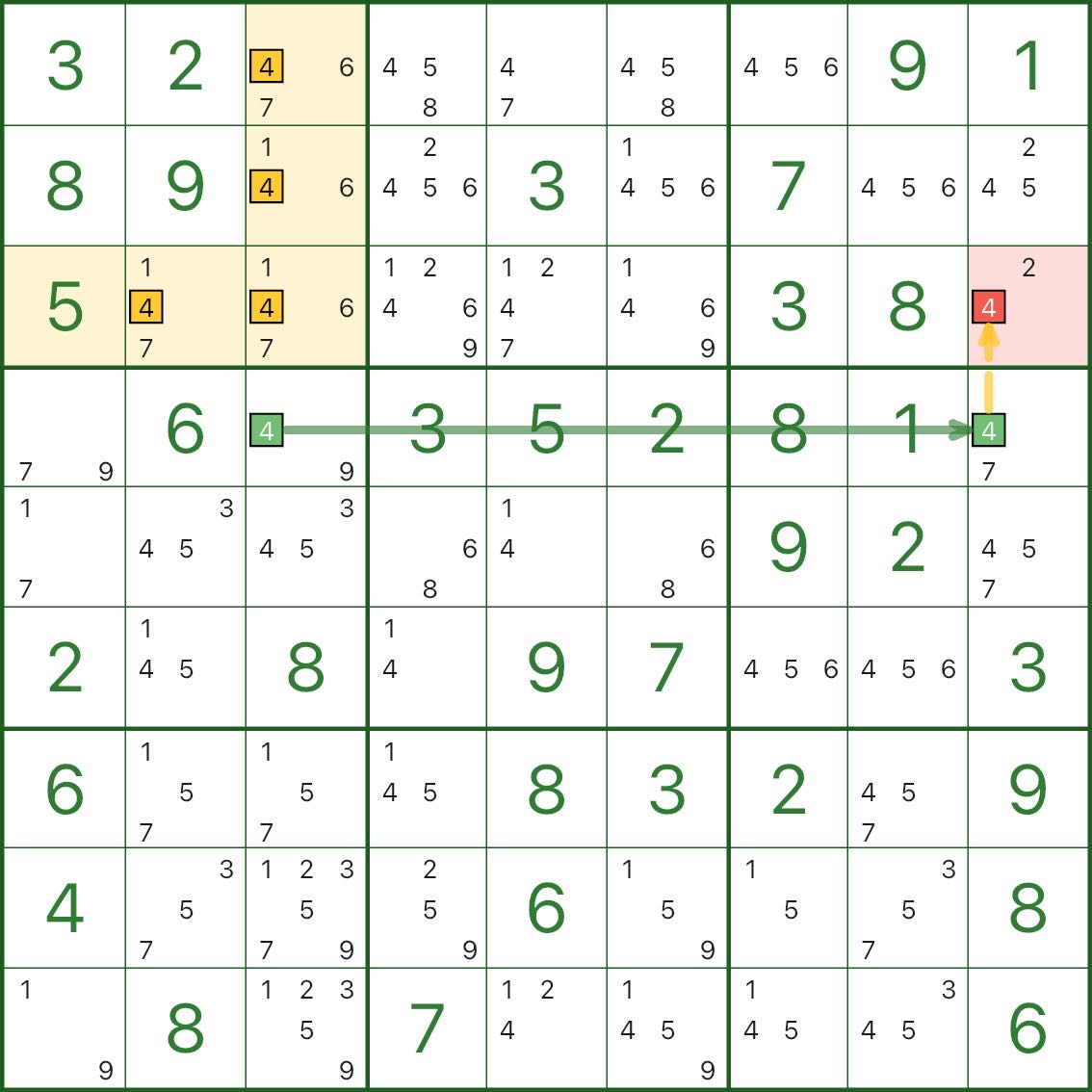
Empty Rectangle example B

Comment trouver un rectangle vide

Liste de contrôle en une ligne : trouver une boîte où d candidats forment une forme de croix/L, puis utiliser une chaîne courte qui ferait manquer de place à la boîte pour d, et éliminerait le candidat rouge par contradiction.

Dans un vrai casse-tête :

Choisissez un chiffre d
Dans une case, vérifiez si tous les d candidats se trouvent sur une ligne + une colonne (forme en croix/L)
Recherchez une chaîne courte afin que, en supposant qu'un candidat rouge soit vrai, force d sur ces lignes
Si cette hypothèse laisse la case sans pas de place pour d, éliminez le candidat rouge d