Grue

Prérequis : Chain Basics

Description

Crane est une courte technique d'élimination des candidats à un chiffre : concentrez-vous sur un chiffre d.

Il ressemble beaucoup à un cerf-volant, mais avec une différence essentielle :

• Kite : la « connexion box » est un lien faible
• Crane : un des liens forts est à l'intérieur d'une boîte (un lien fort de boîte)

---

Explication

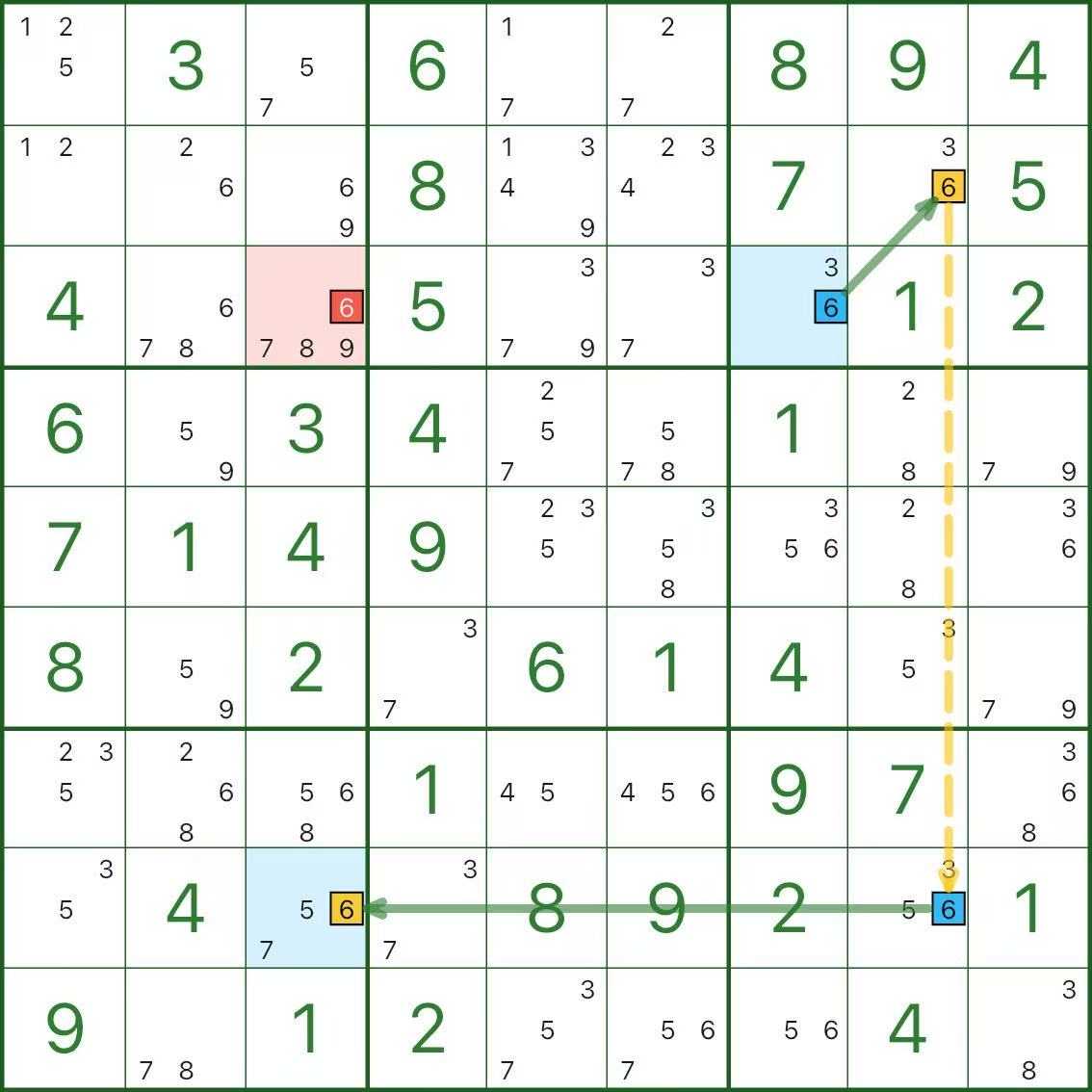
Dans l'image ci-dessus, le chiffre cible est 6.
La chaîne est r3c7 → r2c8 → r8c8 → r8c3. Le candidat rouge est le chiffre 6 dans r3c3 et les deux points finaux sont surlignés en bleu.

Pourquoi peut-on l'éliminer ? Une courte contradiction suffit :

• Supposons r3c3 = 6 (le candidat rouge est vrai)
• Puis au rang 3, r3c7 ≠ 6
• Dans cette case, le chiffre 6 a exactement deux candidats (r3c7 et r2c8), donc si r3c7 n'est pas 6, r2c8 doit être 6 (lien fort de la case)
• Si r2c8 vaut 6, alors dans la même colonne, r8c8 ≠ 6 (maillon faible)
• Sur la ligne 8, le chiffre 6 a exactement deux candidats (r8c8 et r8c3), donc si r8c8 n'est pas 6, r8c3 doit être 6 (lien fort de la ligne)
• Mais r8c3 et r3c3 sont dans la même colonne, donc ils ne peuvent pas être tous les deux 6 → contradiction

Par conséquent, r3c3 ne peut pas être 6 et le candidat rouge peut être éliminé.

---

Exemples

Les deux images suivantes sont d'autres exemples de grues. Utilisez-les comme références :

---

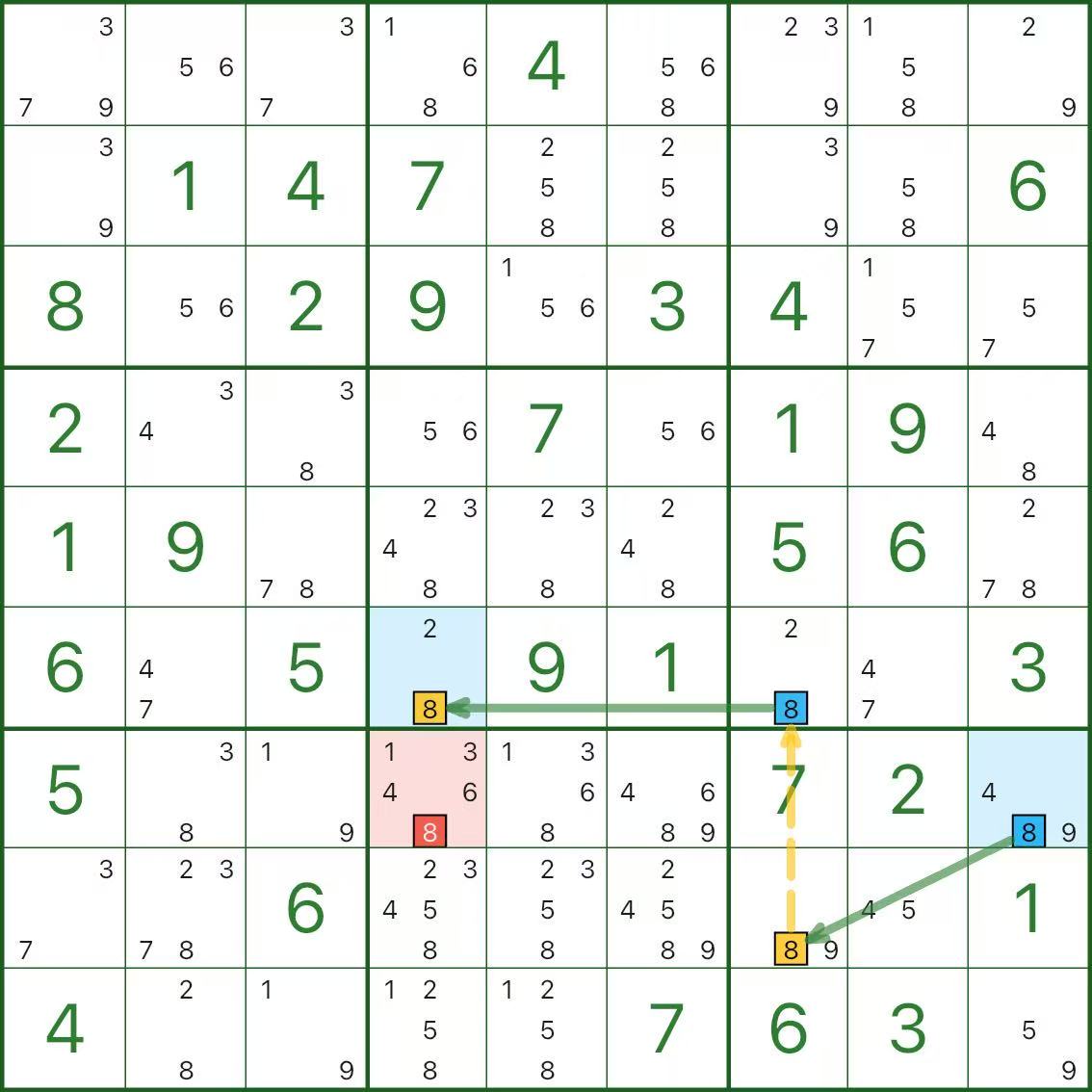
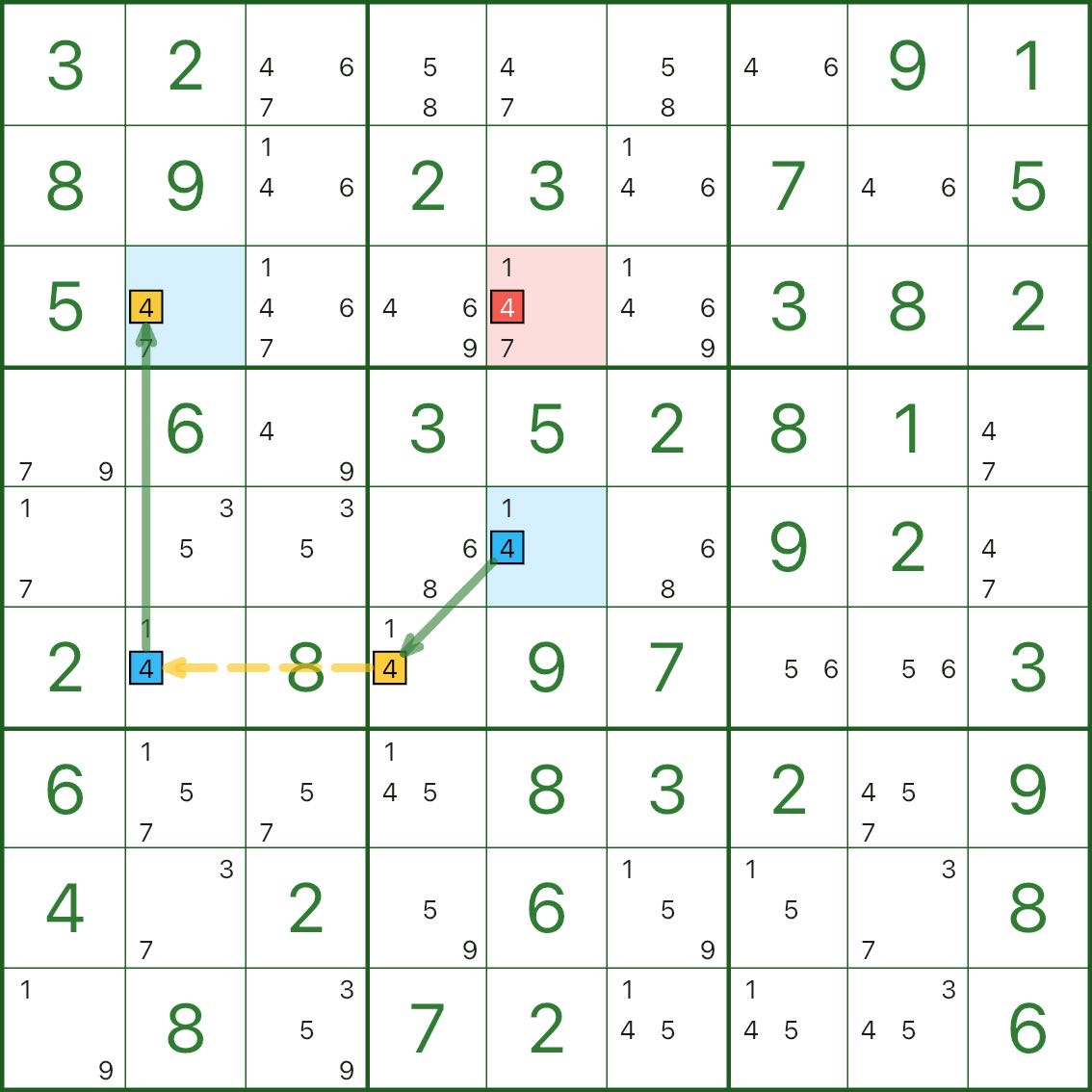
Comment trouver une grue

Liste de contrôle en une ligne : lien fort de boîte + lien fort de ligne/colonne, reliés par un seul maillon faible en forme de L → éliminez l'endroit où les deux points de terminaison sont vus.

Dans un vrai casse-tête :

1. Choisissez un chiffre d
2. Trouvez une case où d apparaît dans exactement 2 cellules candidates (lien fort de la case)
3. Recherchez une ligne ou colonne où d apparaît également dans exactement 2 cellules candidates (lien fort ligne/colonne)
4. Vérifiez si vous pouvez les relier avec un seul maillon faible (même ligne ou même colonne) pour former un L
5. Les deux points finaux restants sont les points finaux : éliminez d de toute cellule qui peut voir les deux points finaux