Coloration de base

Prérequis : Chain Basics

Description

La coloration de base est une technique d'élimination de candidats à un chiffre : concentrez-vous sur un chiffre d et utilisez uniquement des liens forts provenant de bilocations (une ligne/colonne/boîte où le chiffre d apparaît dans exactement deux cellules candidates).

Vous « colorez » les candidats selon des liens forts en utilisant deux couleurs (bleu/jaune).
Ces deux couleurs représentent deux voies de déduction mutuellement exclusives : sur un lien fort, exactement une extrémité est vraie, donc la couleur alterne.

Dans une chaîne colorée, vous pouvez considérer le bleu/jaune comme deux hypothèses opposées :

• Supposons que le bleu est vrai ⇒ le jaune est faux
• Supposons que le bleu est faux ⇒ le jaune est vrai

Donc dans le même lien fort, une des deux couleurs doit être vraie.

La coloration de base conduit généralement à deux types de conclusions :

1. Piège : un candidat rouge peut voir un candidat bleu et un candidat jaune → le candidat rouge peut être éliminé
2. Contradiction de même couleur : deux candidats de la même couleur apparaissent dans une maison → cette couleur entière est impossible et peut être éliminée

---

Piège

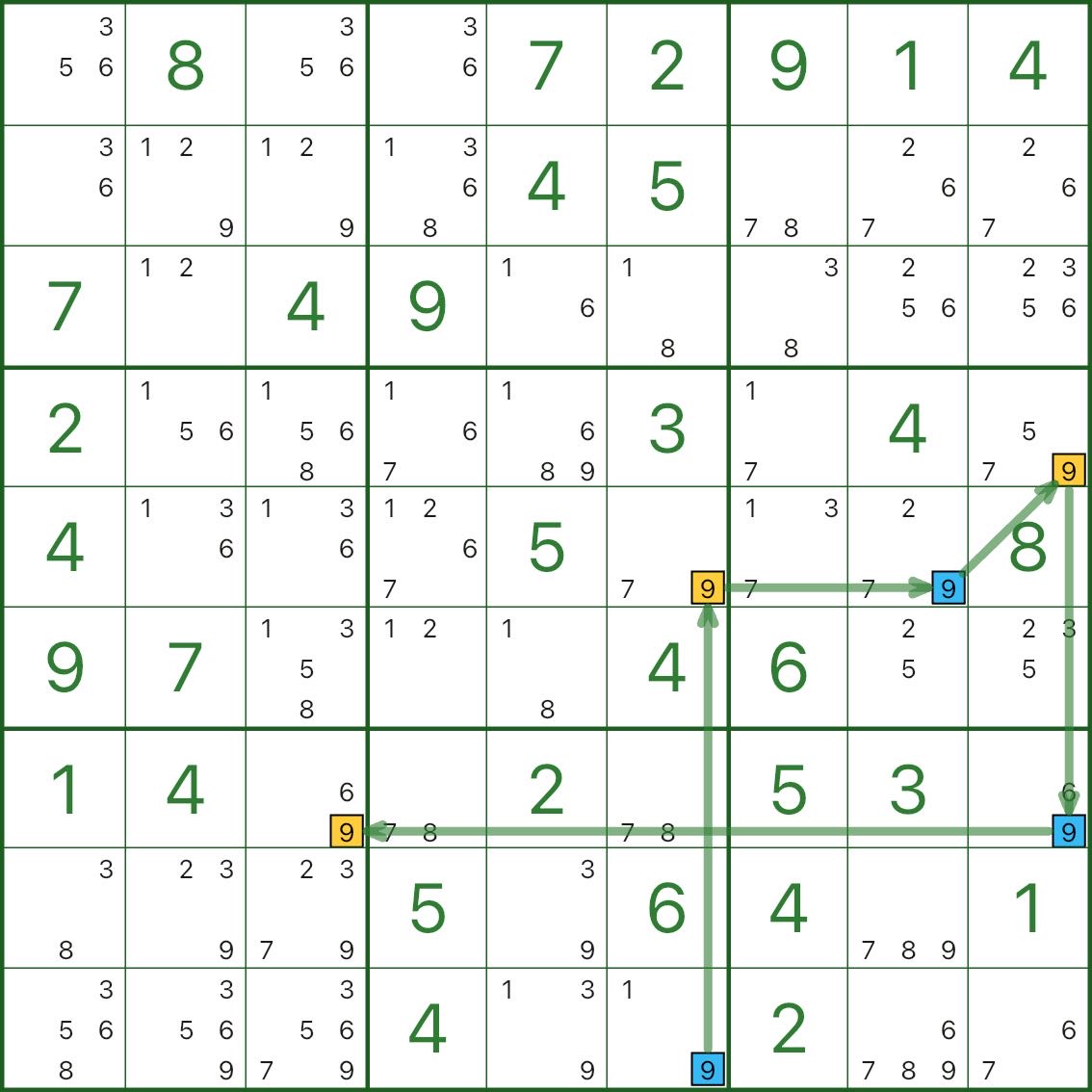
Dans l'image 1, le chiffre cible est 9. Nous colorons une chaîne à maillons forts à partir de r9c6 ; l'autre point de terminaison est r7c3 (bleu/jaune).

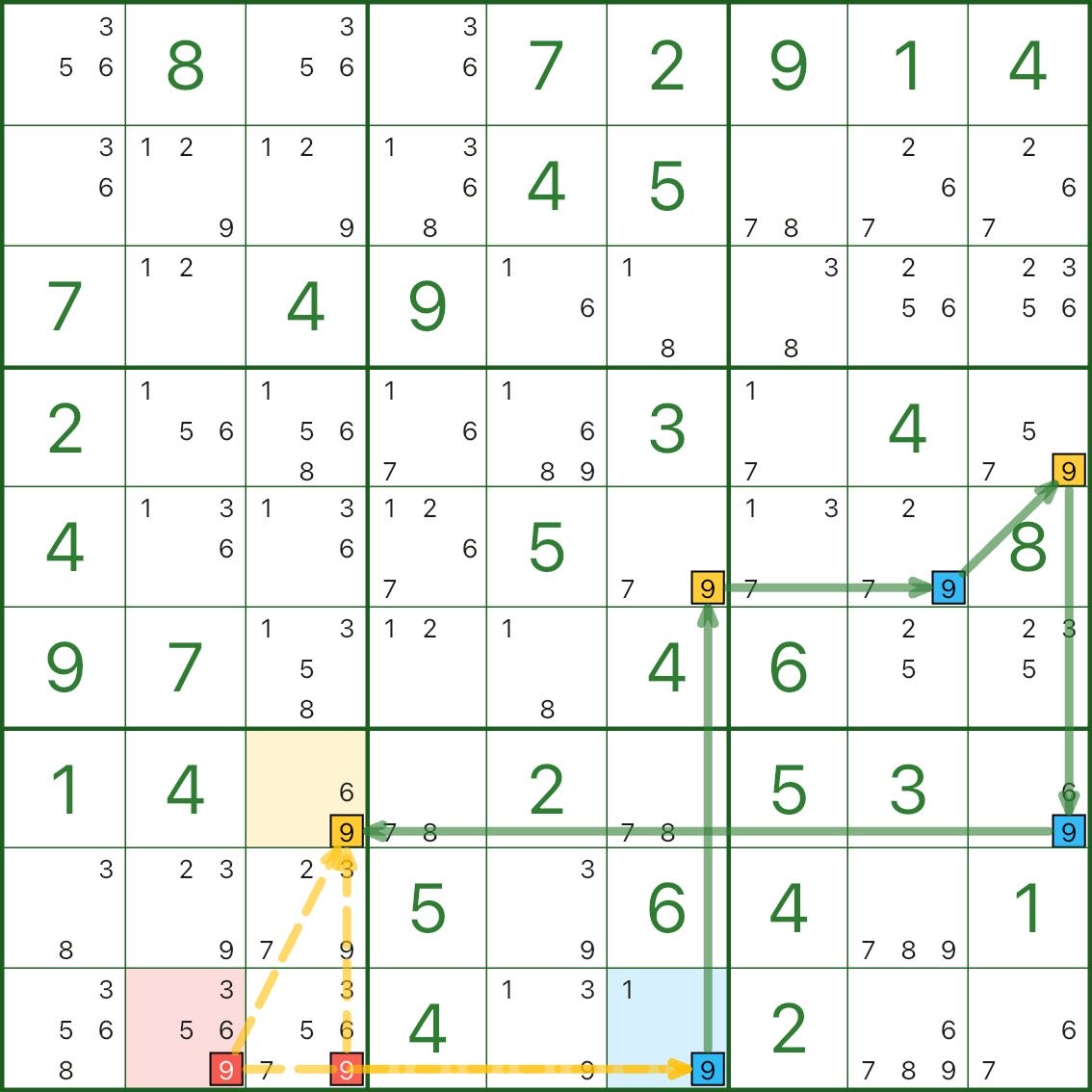
Dans l'image 2, les candidats rouges sont le candidat 9 en r9c2 et le candidat 9 en r9c3.
Pourquoi peut-on les supprimer ? L'idée clé est la suivante :

• Si bleu est vrai, le point final bleu (par exemple r9c6) est 9. Puisque les candidats rouges peuvent le voir, ils sont en conflit avec le point final bleu et ne peuvent pas être 9.
• Si bleu est faux, alors sur le même lien fort, le point final jaune doit être vrai (par exemple, r7c3 vaut 9). Les candidats rouges peuvent également le voir, ils sont donc toujours en conflit et ne peuvent pas être 9.

Dans tous les cas, les candidats rouges ne peuvent pas être au nombre de 9, ils peuvent donc être éliminés.

---

Contradiction de même couleur

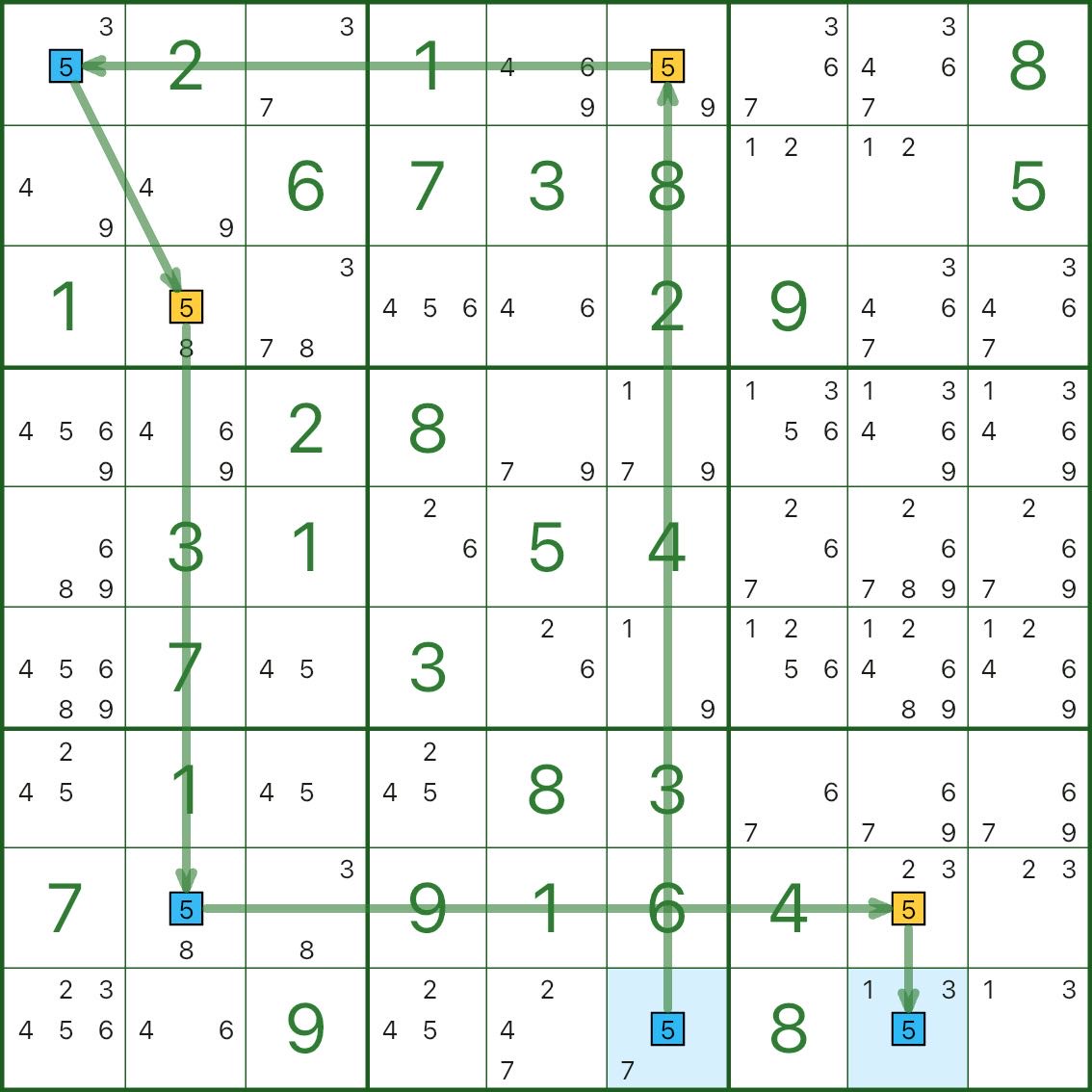
Dans l'image 3, le chiffre cible est 5. À partir de r9c6, la chaîne force finalement r9c8 à être également un 5 bleu.
Mais r9c6 et r9c8 sont dans la même rangée, donc ils ne peuvent pas tous les deux avoir la valeur 5 — c'est une contradiction de même couleur.

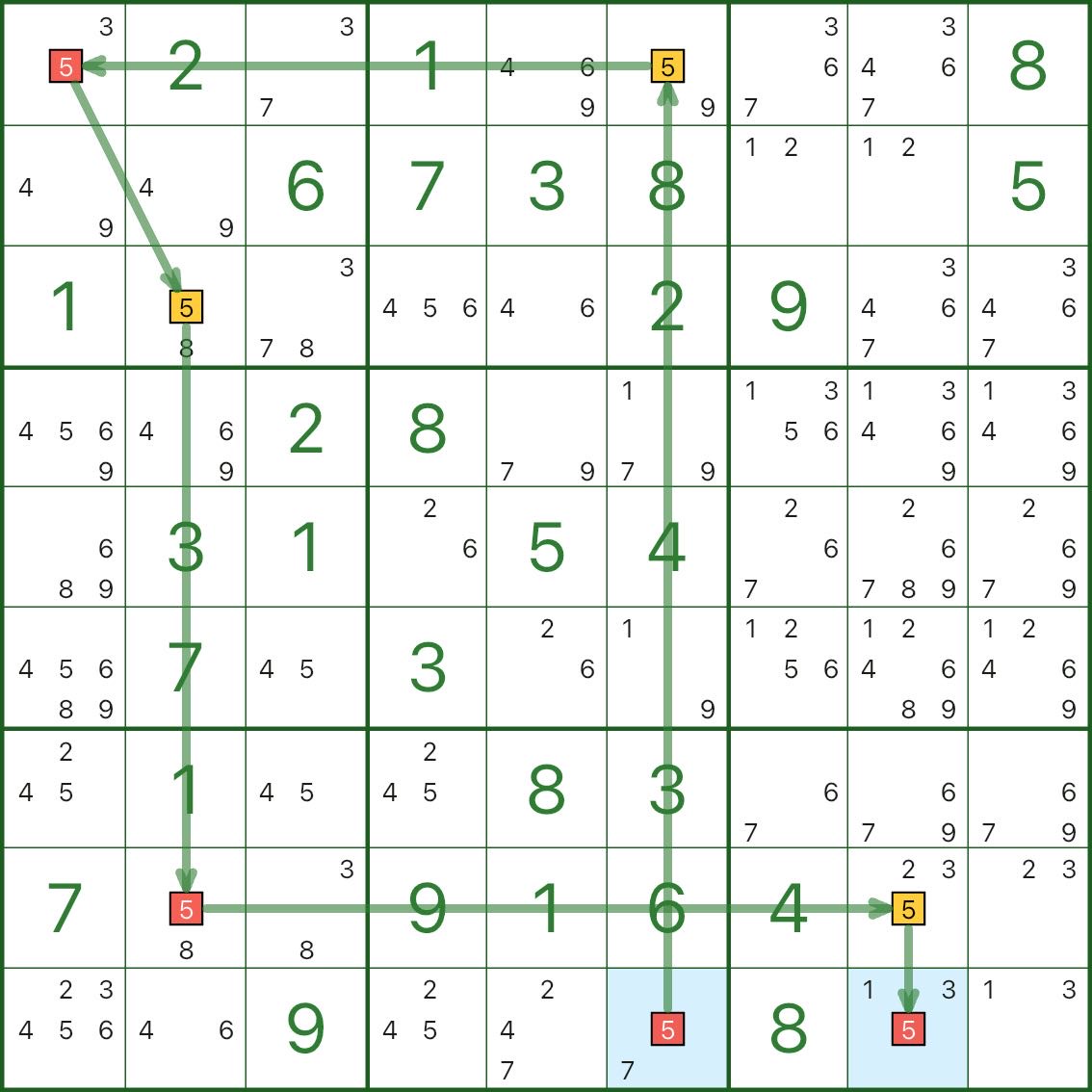
Le parcours bleu est donc impossible :
tous les candidats bleus 5 peuvent être éliminés (illustré dans l'image 4).

---

Comment trouver une coloration de base

Liste de contrôle en une ligne : trouvez les liens forts de bilocation, coloriez-les en bleu/jaune, puis recherchez les pièges ou les contradictions de même couleur.

Dans un vrai casse-tête :

1. Choisissez un chiffre d
2. Trouver les liens forts de bilocation pour d (une unité avec exactement 2 candidats de d)
3. Commencez n’importe où et alternez les couleurs le long de liens forts
4. Recherchez :
   • un candidat rouge qui voit un bleu et un jaune → élimination piège
   • deux candidats de même couleur dans une unité → éliminez toute cette couleur