Bases de la chaîne

Liens forts / liens faibles / alternance (AIC)

Les chaînes sont un élément essentiel de nombreuses techniques avancées de Sudoku.
Au fond, une chaîne n'est qu'une séquence d'implications « si… alors… » qui permet aux déductions de voyager à travers la grille.

Après ce chapitre, les astuces avancées telles que les chaînes à un chiffre, le cerf-volant, le gratte-ciel, la méduse et l'AIC sembleront beaucoup plus lisibles.

Nous utilisons r1c1 pour faire référence à une position de cellule :
r = ligne, c = colonne.

Pour rendre les diagrammes plus faciles à suivre, nous utilisons :

• Ligne continue verte : lien fort
• Ligne pointillée jaune : maillon faible
• Fond candidat Bleu/Jaune : deux « états » mutuellement exclusifs, pour visualiser l'alternance
• Candidat rouge : le candidat à éliminer dans cette étape

Rappel : une chaîne est bidirectionnelle. Les flèches servent uniquement à la lisibilité.

---

Qu'est-ce qu'une chaîne ?

En bref, une chaîne relie les relations entre candidats afin que vous puissiez continuer à appliquer la logique « si… alors… » :

Si A n’est pas possible, alors B doit être vrai ;
si B est vrai, alors C doit être faux ;
…

Une chaîne est composée de :

• Nœuds : candidats (un chiffre candidat dans une cellule)
• Liens : relations entre candidats (forts / faibles)

Une chaîne ne veut pas forcément dire « on supprime toujours le départ ». Il s’agit plutôt d’un cheminement de raisonnement :

• Atteignez une contradiction ⇒ prouver qu'un candidat ne peut pas être vrai → éliminez-le
• Atteindre une vérité forcée ⇒ prouver qu'un candidat doit être vrai → attribuer une valeur

Cet article se concentre sur les « chaînes à un chiffre » les plus courantes : le raisonnement sur les candidats à un chiffre d.
(Les relations entre cellules bivaleurs et les liens forts groupés/régionaux sont abordés plus loin.)

---

Liens forts et liens faibles

Lien fort (paire conjuguée)

Mnémonique : soit-ou.

Dans une même unité (ligne/colonne/case), si un chiffre d apparaît dans exactement deux cellules candidates, ces deux candidates forment un lien fort (une paire conjuguée).

L’implication clé est « PAS force OUI » :

• Si PAS A, alors B (Si A n'est pas d, alors B doit être d)
• Si PAS B, alors A

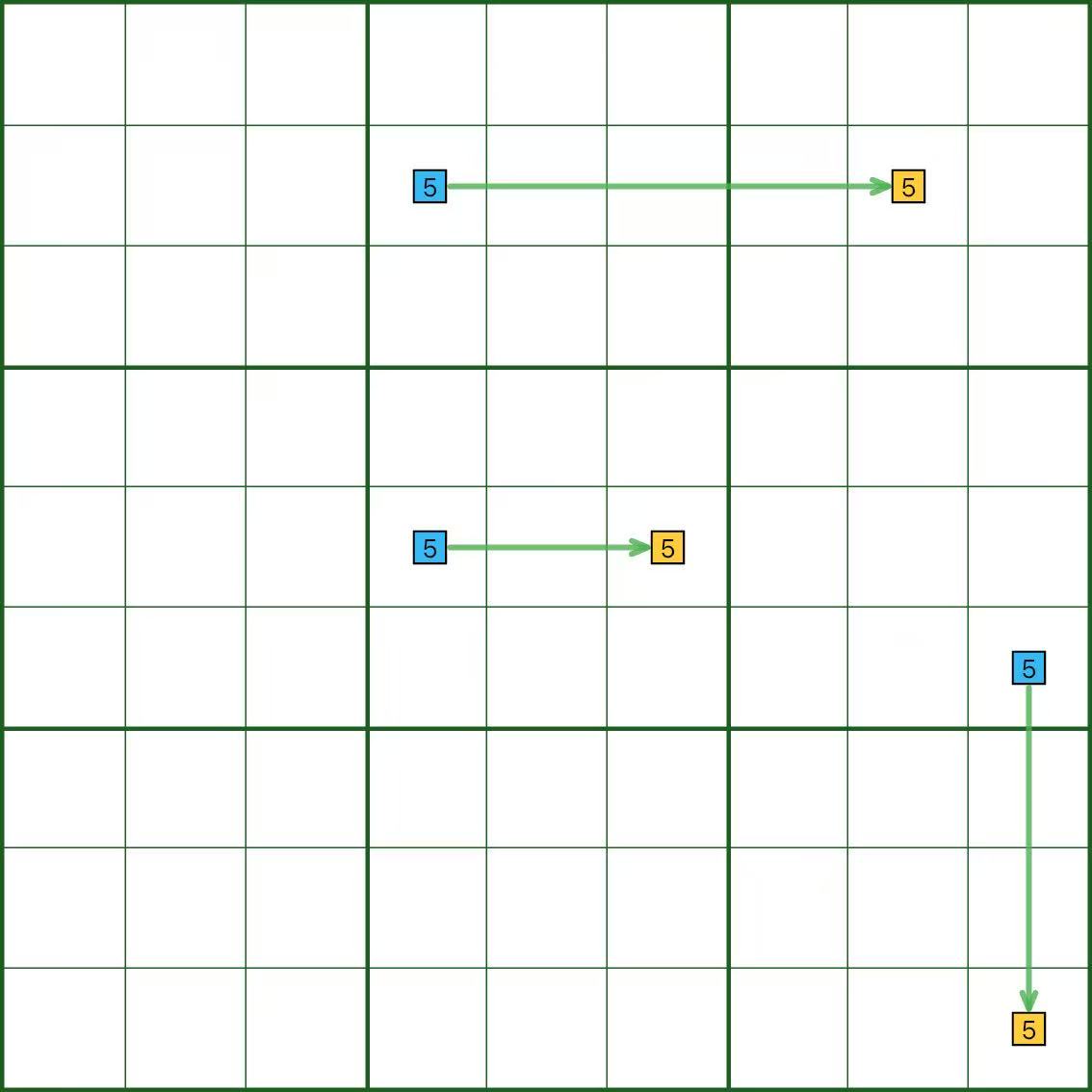
Dans le diagramme, le chiffre 5 forme des liens forts dans une ligne, une colonne et une case.
Vous pouvez le lire des deux côtés ; les flèches ne sont qu'une aide à la lecture.

Remarque importante : chaque lien fort est aussi un maillon faible.
Puisque les deux candidats partagent la même unité, ils ne peuvent pas être tous les deux vrais :

• Si A, alors PAS B (Si A est d, alors B n'est pas d)

Résumé en une ligne :

Lien fort = exclusivité faible + « l'un d'entre eux doit être vrai »

Lien faible

Mnémonique : si vous vous voyez, vous ne pouvez pas être vrais tous les deux.

Un maillon faible exprime une chose :

Deux candidats ne peuvent pas être tous les deux vrais.

Dans les chaînes à un chiffre, le maillon faible le plus courant est constitué de deux candidats du même chiffre d dans la même unité.

Implication:

• Si A, alors PAS B

Mais pas l'inverse :

• Si A est faux, vous ne pouvez pas conclure B (il peut y avoir un troisième point).

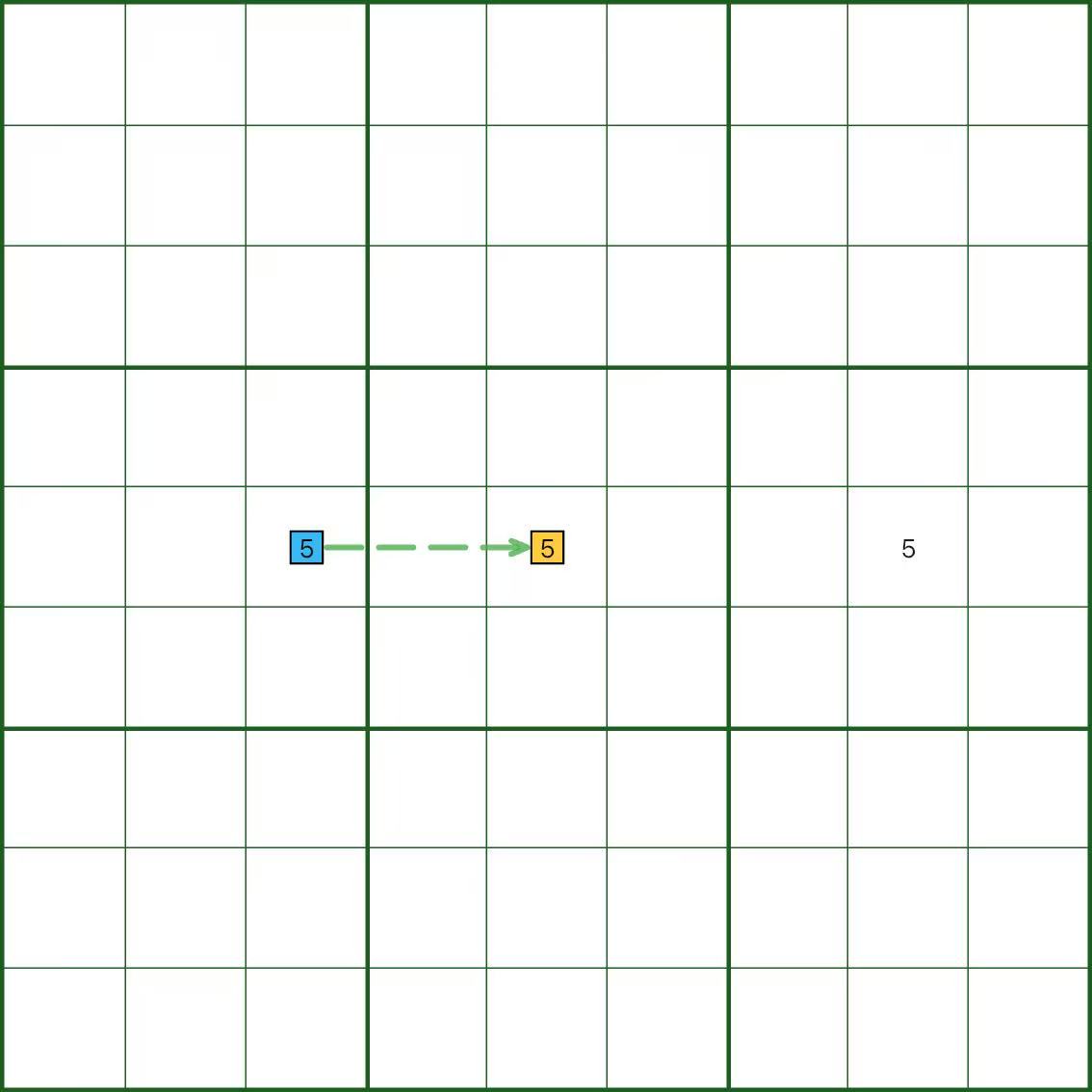
Dans le diagramme, le chiffre 5 comporte trois cellules candidates consécutives, chaque paire est donc faiblement liée.
L'image ne dessine qu'un seul segment en pointillés juste pour montrer à quoi ressemble un maillon faible.

---

Comment fonctionnent les chaînes ?

Pour propager le long d'une chaîne, rappelez-vous deux règles :

1. Vrai → (faible) → Faux
   Les maillons faibles sont exclusifs : si A est vrai, B doit être faux.
2. Faux → (fort) → Vrai
   Les liens forts sont soit-ou : si A est faux, l’autre candidat doit être vrai.

Ainsi, une chaîne de travail alterne généralement :

Faux —(fort)→ Vrai —(faible)→ Faux —(fort)→ Vrai —(faible)→ Faux …

Pourquoi alterner ?

• ruptures faibles-faibles : « faux » ne se propage pas via un maillon faible
• fort-fort peut se connecter, mais dans de nombreuses énigmes, cela correspond souvent à des modèles plus simples, les chaînes sont donc plus utiles pour la propagation alternée

---

Exemple

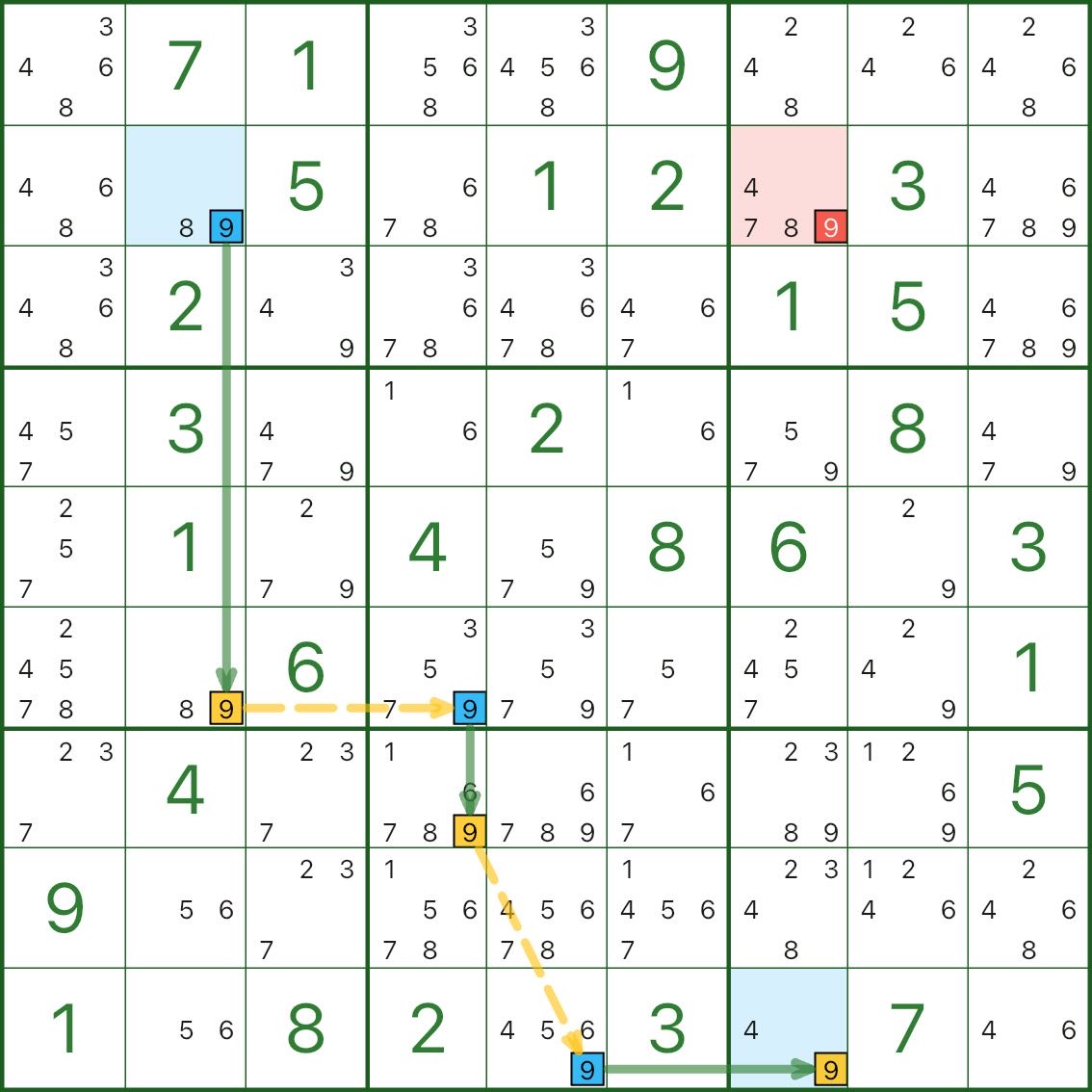
Dans le diagramme, le candidat rouge est le chiffre 9 dans r2c7.

Lisez-le comme ceci :

1. Depuis le début en surbrillance : une fois que r2c2 n'est PAS 9, la chaîne se propage pour forcer r9c7 = 9
   (vous pouvez voir l'alternance propre Faux → Vrai → Faux → Vrai → Faux → Vrai)

2. Utilisez maintenant une contradiction : supposons que le candidat rouge r2c7 = 9 est vrai

   • r2c7 voit r2c2 dans la même ligne, donc r2c2 ne peut pas être 9 (r2c2(9) est faux)
   • propager ce « faux » à travers la chaîne, forçant r9c7(9) à être vrai
   • r2c7 et r9c7 sont dans la même colonne, donc ils ne peuvent pas être tous les deux 9 → contradiction

Par conséquent, r2c7 ne peut pas être 9 et ce candidat rouge peut être éliminé.

---

Pratique

Les trois diagrammes suivants sont tous des chaînes à un chiffre. Prenez votre temps.

Trois questions d'auto-vérification rapides :

1. Quels segments constituent des liens forts, et pourquoi sont-ils « soit l'un soit l'autre » ?
2. Quels segments constituent des maillons faibles et pourquoi s’excluent-ils mutuellement ?
3. Pourquoi le candidat rouge conduit-il à une contradiction ?

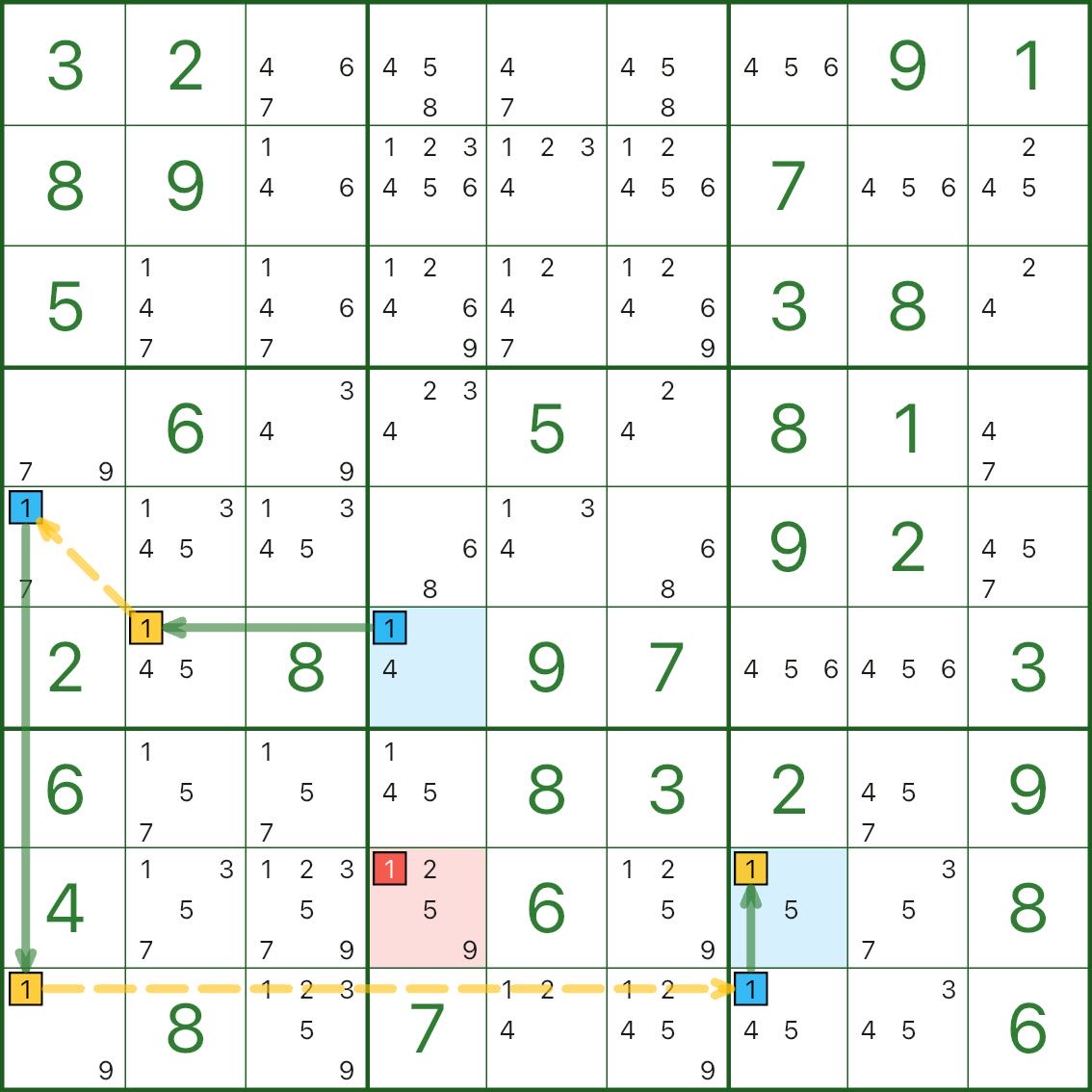
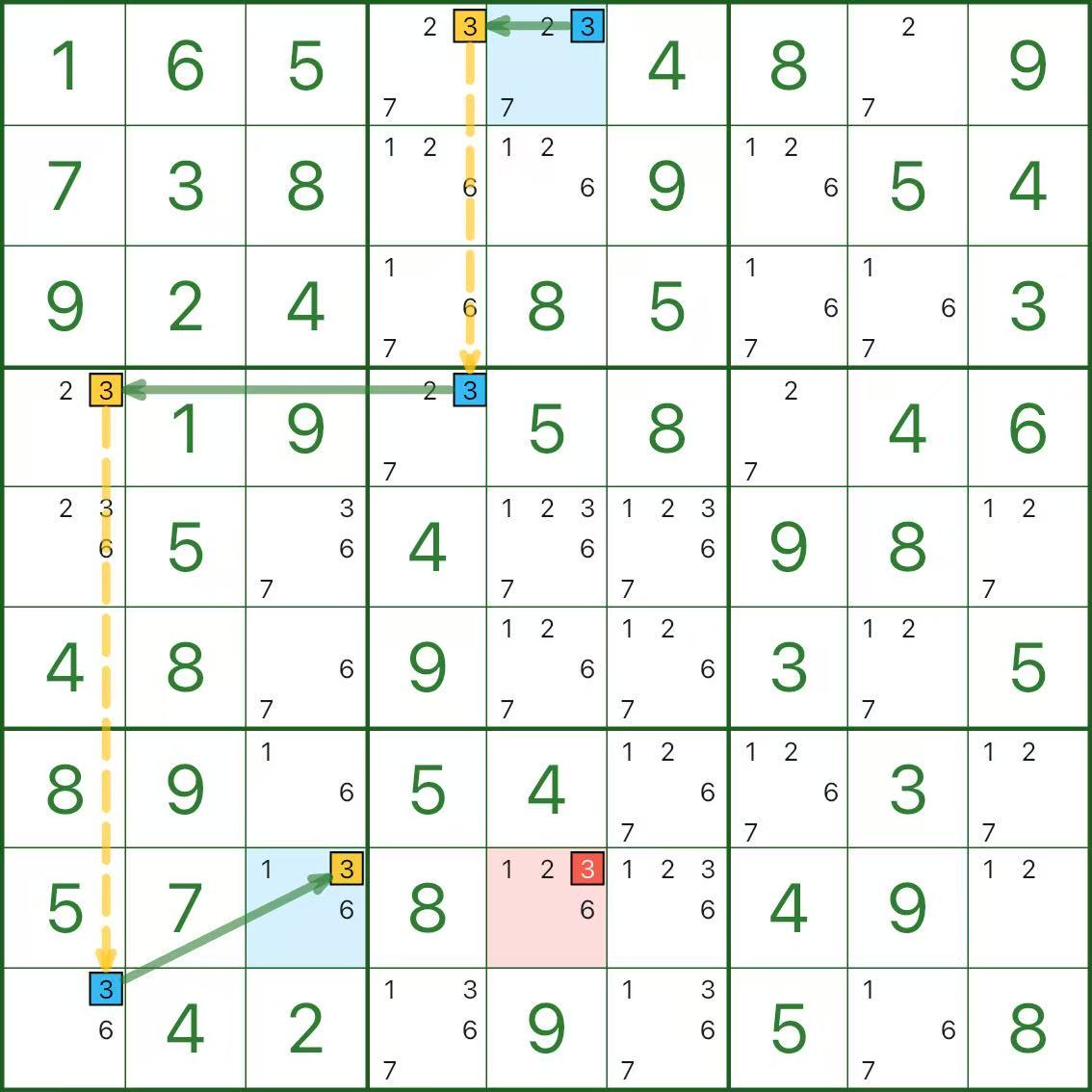
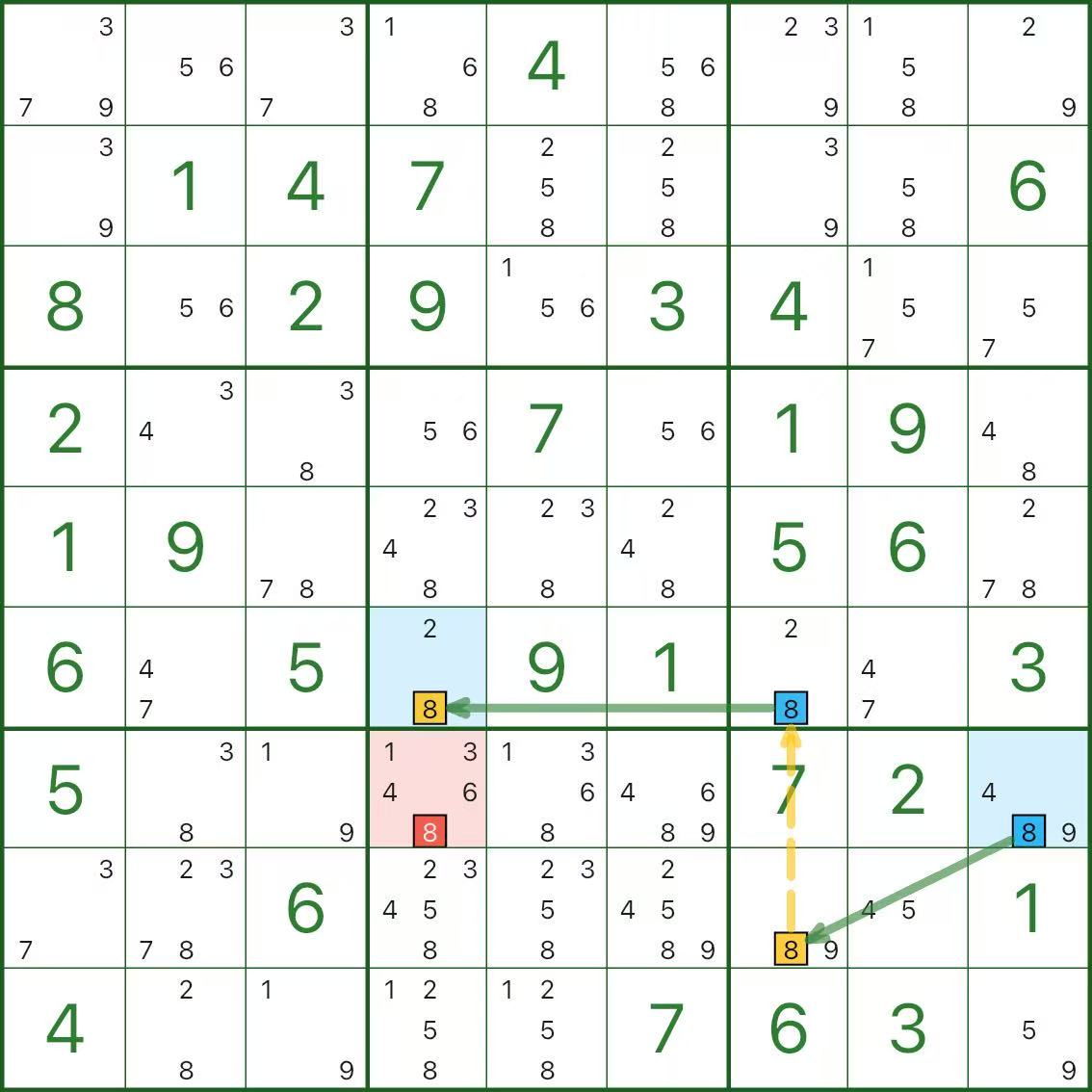
Si cela semble un peu sinueux au début, c’est tout à fait normal.
C’est une chaîne : la base de nombreuses techniques avancées : familiarisez-vous avec elle avant de passer à autre chose.