BOGUE+1

Prérequis : BUG+1 repose sur le fait que le puzzle ait exactement une solution.
Si vous ne l'avez pas encore lu, commencez ici :
Uniqueness

---

1. Aperçu

BUG+1 est l'abréviation de BUG + 1 — vous pouvez également l'entendre appelé Bivalue Universal Grave + 1.

Le nom semble effrayant, mais il décrit un état de carte très spécifique :

• presque toutes les cellules non résolues sont bivaleurs (exactement 2 candidats)
• une "cellule d'exception" a 3 candidats (c'est le "+1")

Qu'est-ce qu'un BUG ?

BUG = Tombe universelle bivaleur.

On l’appelle « tombe » parce que la grille peut sembler « bloquée » : les candidats arrivent par paires partout, et la progression s’arrête souvent sans unicité.

Lorsque la grille satisfait ces deux conditions, elle devient une structure « BUG » très symétrique :

1. chaque cellule non résolue est bivaleur
2. pour n'importe quel chiffre d, dans chaque maison (ligne/colonne/boîte), le nombre de postes candidats pour d est pair
   • le plus souvent 2
   • si d est déjà placé dans cette maison, il peut être 0 (toujours pair)

Cette symétrie permet souvent deux complétions valides (solutions multiples).

Alors, qu'est-ce que BUG+1 ?

BUG+1 est « presque un BUG, mais pas tout à fait » :

• toutes les cellules non résolues sont bivaleurs
  sauf une cellule avec 3 candidats

Ce candidat supplémentaire brise la symétrie paire – et c’est exactement ce qui nous permet de forcer un placement en utilisant l’unicité.

La cellule d'exception a donc un candidat forcé — nous pouvons placer le chiffre directement.

---

2. Procédure pas à pas

Étape 1 : repérer l'état « presque tous bivaleurs » (image du haut)

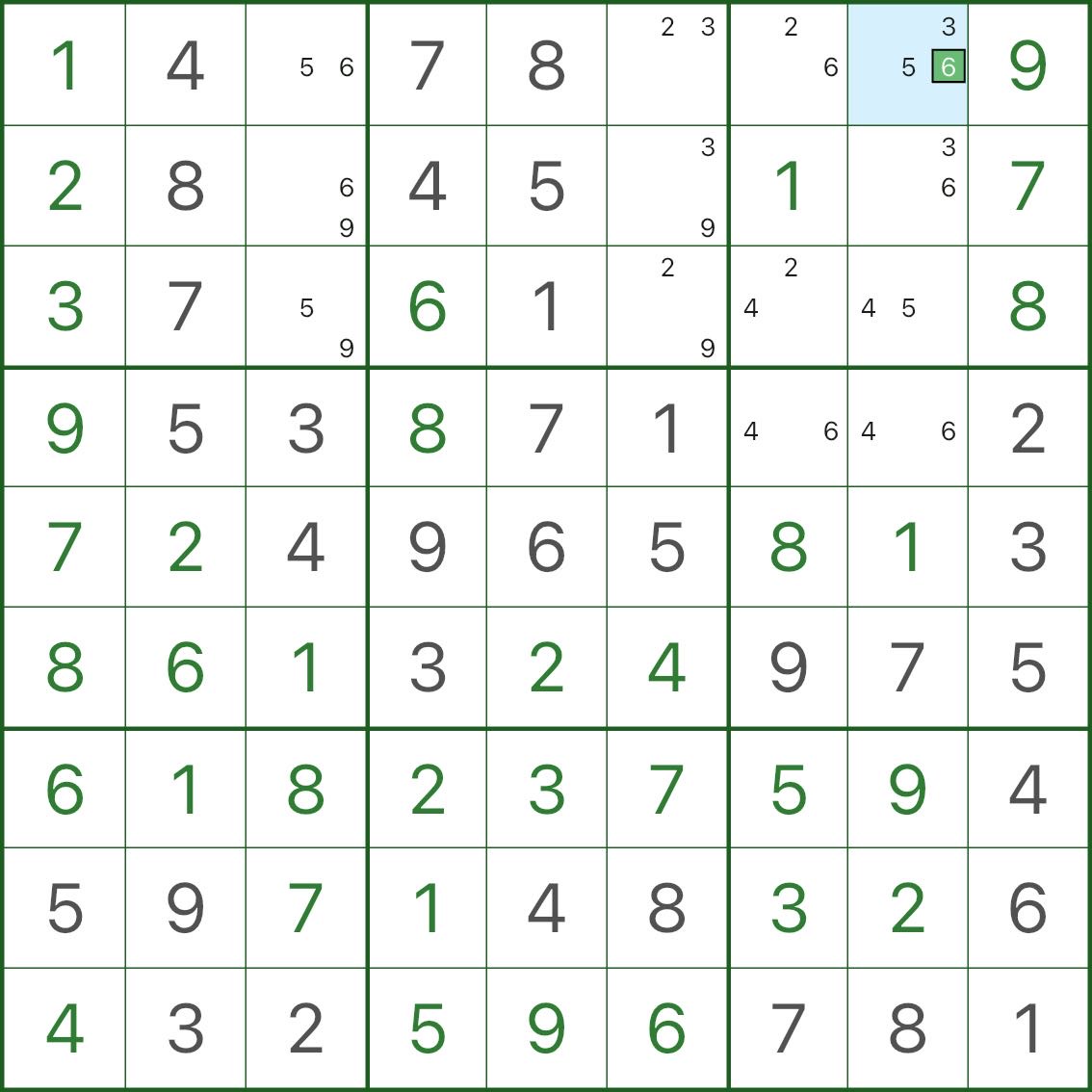
Dans l'image :

• la plupart des cellules vides affichent seulement 2 petits candidats
• une cellule fait exception, affichant 3 candidats (le « +1 »)

Étape 2 : quel chiffre doit-on placer ? (et pourquoi ?)

Nous nous concentrons uniquement sur les trois candidats dans la cellule d'exception et nous faisons une chose simple : vérifier impair vs pair.

Comment :

1. regardez les trois candidats dans la cellule d'exception
2. pour chacun de ces chiffres, comptez combien de fois il apparaît comme candidat dans la ligne/colonne/case de la cellule d'exception

Vous constaterez généralement qu'un chiffre apparaît 3 fois (impair) dans l'une de ces maisons.
Ce candidat « impair » est le chiffre que vous devez placer.

Pourquoi? Utilisez une contradiction :

Supposons que nous ne placions pas ce candidat « impair », mais choisissons plutôt l'un des deux autres candidats « pairs » :

1. la cellule d'exception devient bivaleur
2. la répartition des candidats entre les maisons revient à une symétrie « paire » (une structure BUG)
3. Les structures BUG permettent souvent deux complétions valides (plusieurs solutions)

Mais le puzzle doit être unique, ce qui rend le choix impossible.
Par conséquent, le candidat « impair » doit être vrai — c'est le chiffre que vous placez.

Si vous ne souhaitez rien compter : l’indice mettra en évidence pour vous le candidat forcé.

---

3. Exemple

L'image ci-dessous montre le résultat : le candidat forcé « +1 » dans la cellule d'exception est placé.

---

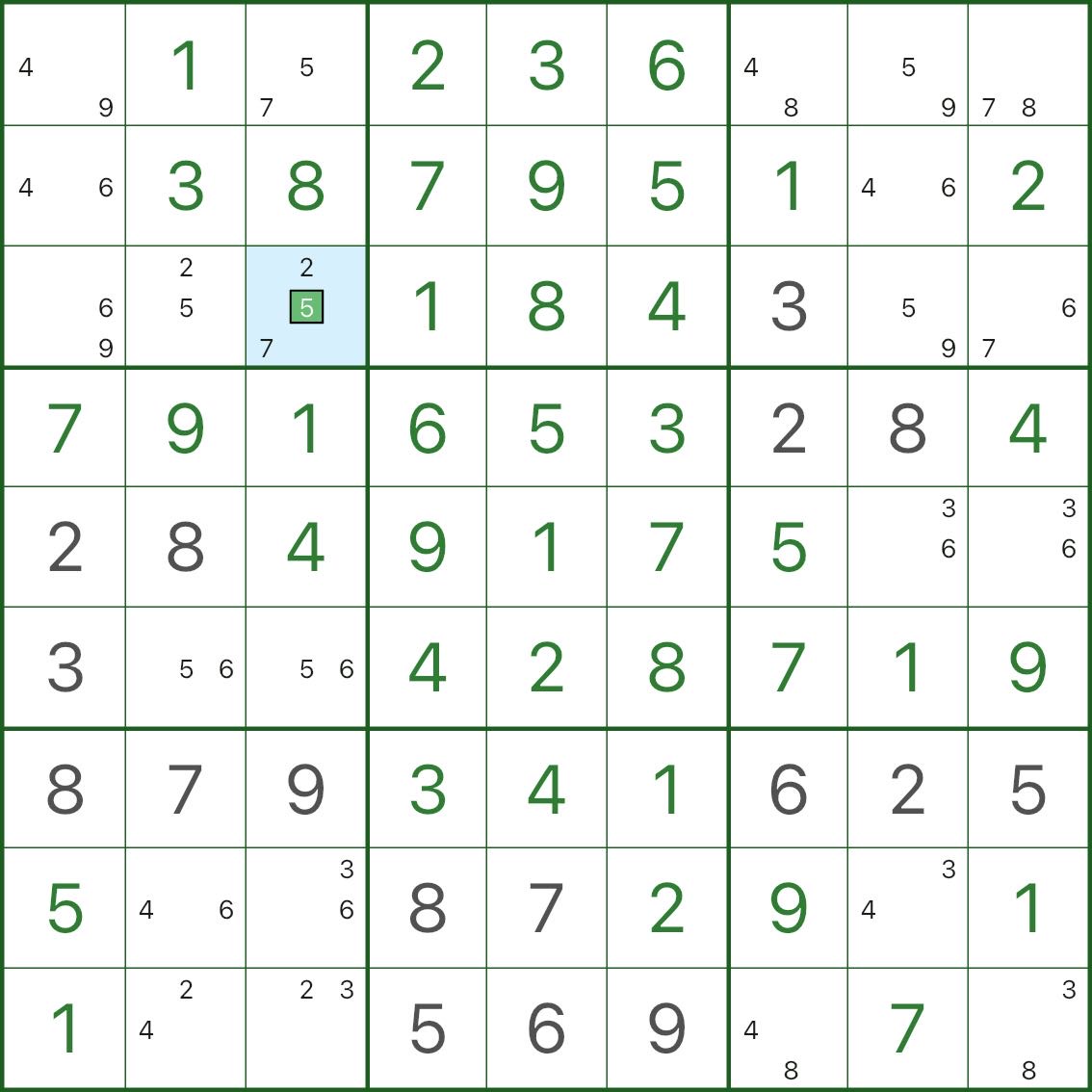
4. Comment repérer le BUG+1

Utilisez cette liste de contrôle :1) Assurez-vous que vos notes de candidats sont complètes et fiables (générez des candidats complets si nécessaire)
2) Recherchez une grille où :

• toutes les cellules non résolues sont bivaleurs
• exactement une cellule contient 3 candidats

3. Dans la ligne/colonne/boîte de cette cellule, comptez les occurrences candidates pour ces trois chiffres : le impair (généralement 3) est le chiffre forcé
4. L'indice mettra en évidence la cellule d'exception et montrera quel candidat est forcé

Remarque : BUG+1 est une technique basée sur l'unicité : elle ne s'applique que lorsqu'il est garanti que le puzzle a une solution unique.