Guías / Ala XYZ
Ala XYZ
XYZ-Wing es similar a <strong>XY-Wing</strong>: ambos utilizan un patrón de “pivote + dos alas” para eliminar a un candidato compartido por contradicción.
Advanced
Ala XYZ
Descripción
XYZ-Wing es similar a XY-Wing: ambos utilizan un patrón de “pivote + dos alas” para eliminar a un candidato compartido por contradicción.
La diferencia clave es que el pivote tiene tres candidatos en XYZ-Wing, por lo que la celda de eliminación normalmente necesita ver el pivote y ambas alas (porque el candidato compartido también podría colocarse en el pivote).
La estructura se ve así (centrándose en el candidato compartido z):
- Pivote (azul): candidatos x, y, z
- Alas (amarillas): {x, z} y {y, z}
Conclusión: en cualquier celda que pueda ver el pivote y ambas alas, el candidato z puede ser eliminado.
Explicación
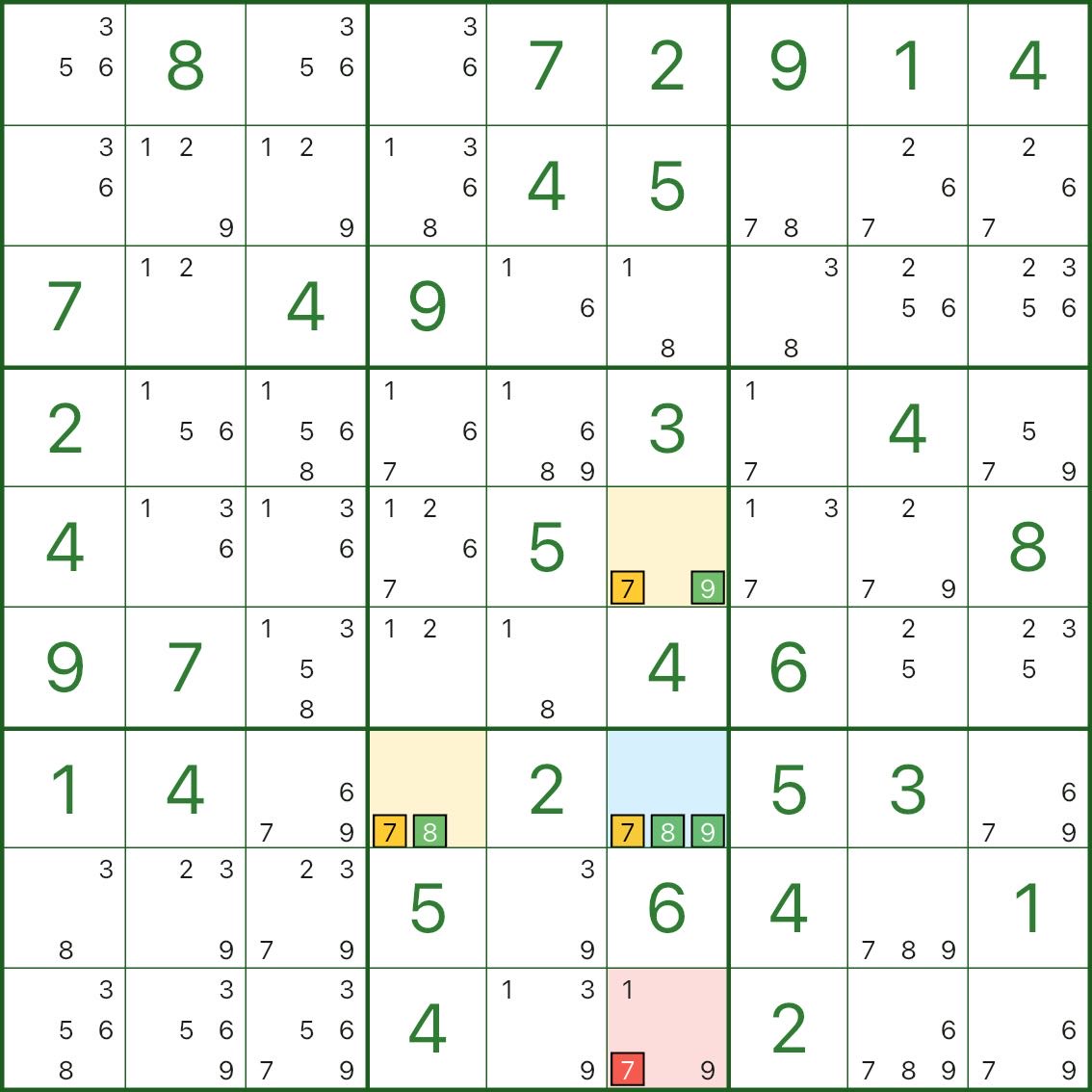
En la imagen de arriba, queremos eliminar el candidato 7 en r9c6 (rojo).
El pivote azul es r7c6, con candidatos 7, 8, 9.
Las dos alas amarillas son:
- r5c6: candidatos 7 y 9
- r7c4: candidatos 7 y 8
¿Por qué podemos eliminar 7 de r9c6? Una breve contradicción es suficiente:
- Supongamos r9c6 = 7 (el candidato rojo es verdadero)
- r9c6 puede ver ambas alas, por lo que 7 se elimina de ambas alas:
- r5c6 debe ser 9
- r7c4 debe ser 8
- Ahora al pivote r7c6 ya no le queda valor:
- r9c6 = 7 ⇒ r7c6 no puede ser 7 (misma columna)
- r5c6 = 9 ⇒ r7c6 no puede ser 9 (misma columna)
- r7c4 = 8 ⇒ r7c6 no puede ser 8 (misma fila)
- r7c6 solo tenía {7,8,9} ⇒ ningún valor encaja (contradicción)
Entonces la suposición es imposible: r9c6 no puede ser 7 y el candidato 7 puede eliminarse.
Ejemplos
Estas imágenes muestran más patrones de alas XYZ. Intenta detectar la misma estructura: pivote (azul) / dos alas (amarilla) / eliminación (roja).
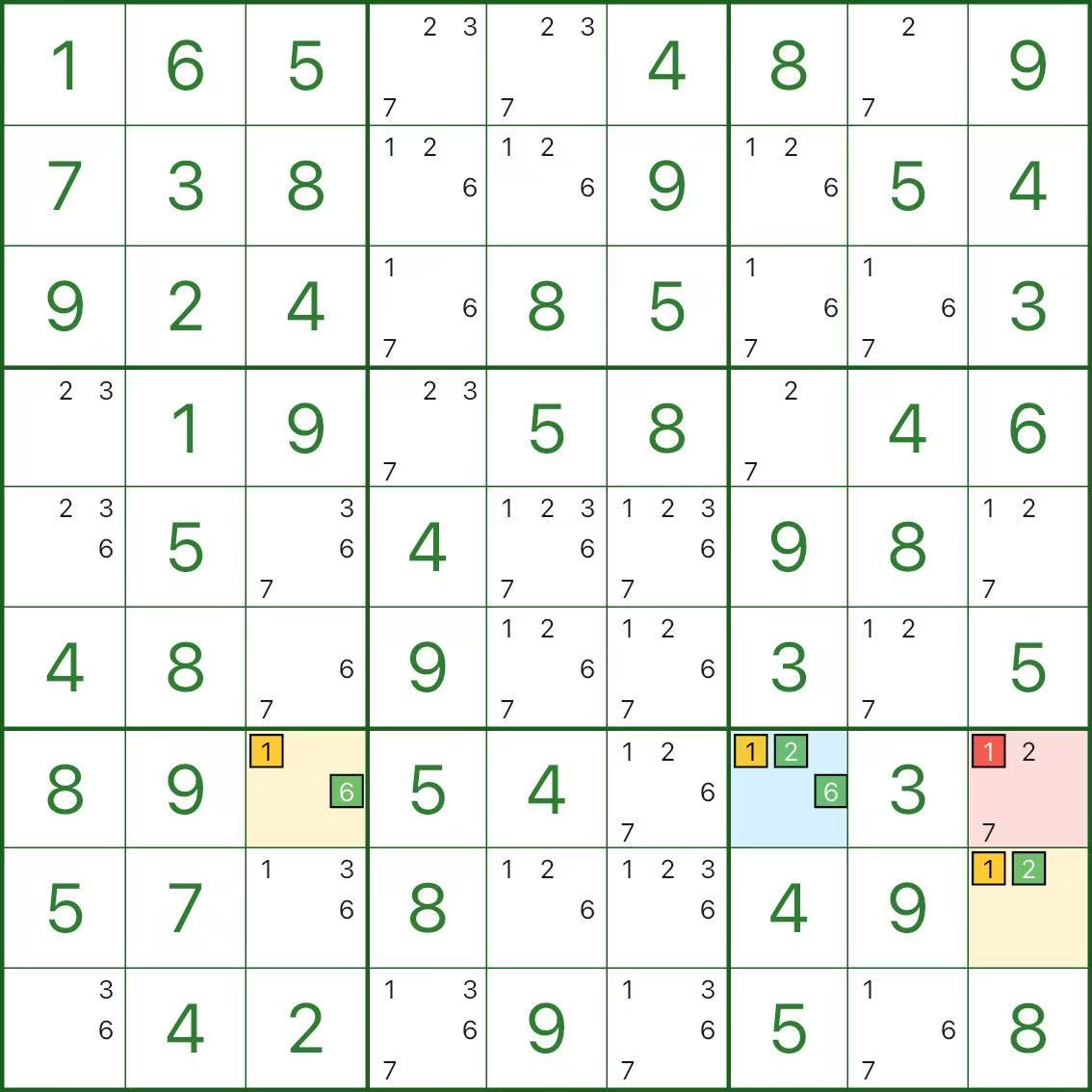
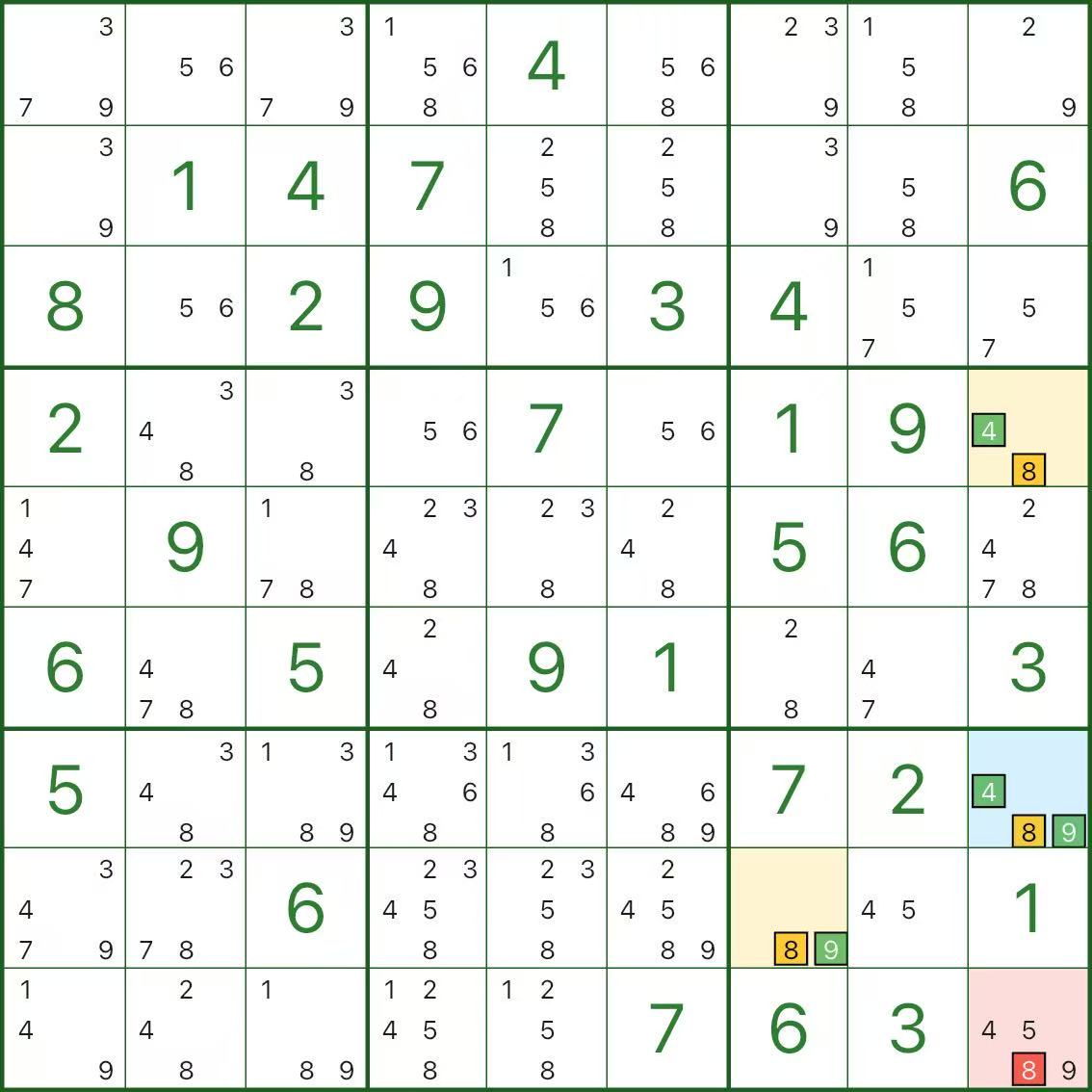
Cómo encontrar el ala XYZ
Lista de verificación de una línea: encuentre un pivote de 3 candidatos {x,y,z}, encuentre dos alas bivalor {x,z} y {y,z}, luego elimine z de cualquier celda que vea el pivote y ambas alas.
En un verdadero rompecabezas:
- Encuentre una celda con exactamente tres candidatos como pivote (azul)
- Encuentre dos celdas que puedan ver el pivote, cada una con exactamente dos candidatos, con forma de {x,z} e {y,z} (amarillo)
- Busque una celda que pueda ver el pivote y ambas alas: elimine el candidato z allí (rojo)