Rectángulo único (UR)

Requisito previo: UR se basa en el hecho de que el rompecabezas tiene exactamente una solución.
Si aún no lo has leído, empieza aquí:
Uniqueness

---

1. Descripción general

Unique Rectángulo (UR) es una familia de técnicas que utiliza la propiedad solución única para eliminar candidatos (y, a veces, colocar un número).

Se centra en una “forma peligrosa”:

• cuatro celdas forman un rectángulo de 2×2 (dos filas × dos columnas, que abarcan exactamente dos cuadros)
• las cuatro esquinas contienen los mismos dos candidatos principales (por ejemplo, 1 y 7)

Si dejamos esas cuatro celdas solo con ese par, el rectángulo a menudo se puede llenar de dos maneras diferentes (intercambiando los dos dígitos), lo que rompería la unicidad.
Entonces, bajo el supuesto de unicidad, podemos concluir: algunos candidatos deben eliminarse o una celda debe tomar un valor específico.

---

2. Tutorial (5 tipos)

Las 5 imágenes a continuación corresponden a los 5 tipos de UR comunes (las sugerencias en la aplicación las etiquetan como Tipo I-V).

Guía de colores:

• Celdas azules: el rectángulo UR (la estructura central)
• Marcas amarillas: candidatos en los que nos centramos en el razonamiento
• Marcas rojas: candidatos a eliminar/o una celda que se puede configurar

Tipo I: techo único → un valor forzado

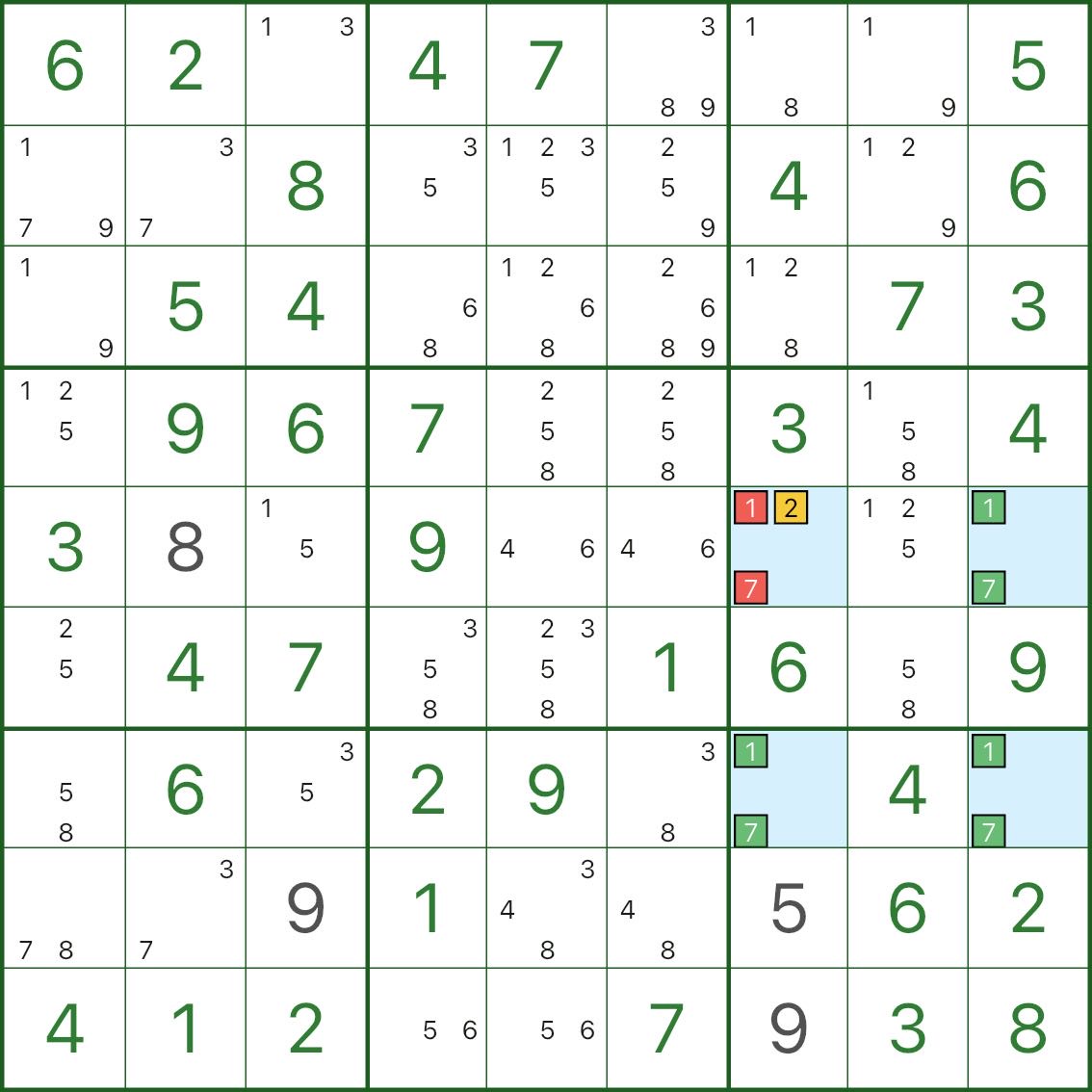
Mire las cuatro celdas azules: forman un rectángulo y todas contienen candidatos 1 y 7.
La celda r5c7 también tiene un candidato adicional 2.

Si 2 no es verdadero en r5c7, entonces r5c7 se quedaría con solo 1 y 7.
Eso haría que las cuatro esquinas fueran "solo {1,7}", permitiendo dos rellenos intercambiables (rompiendo la unicidad).

Entonces bajo unicidad:

• r5c7 no puede retener a los candidatos 1 y 7
• por lo tanto r5c7 debe ser 2

---

Tipo II: dos techos → eliminar c que ve ambos techos

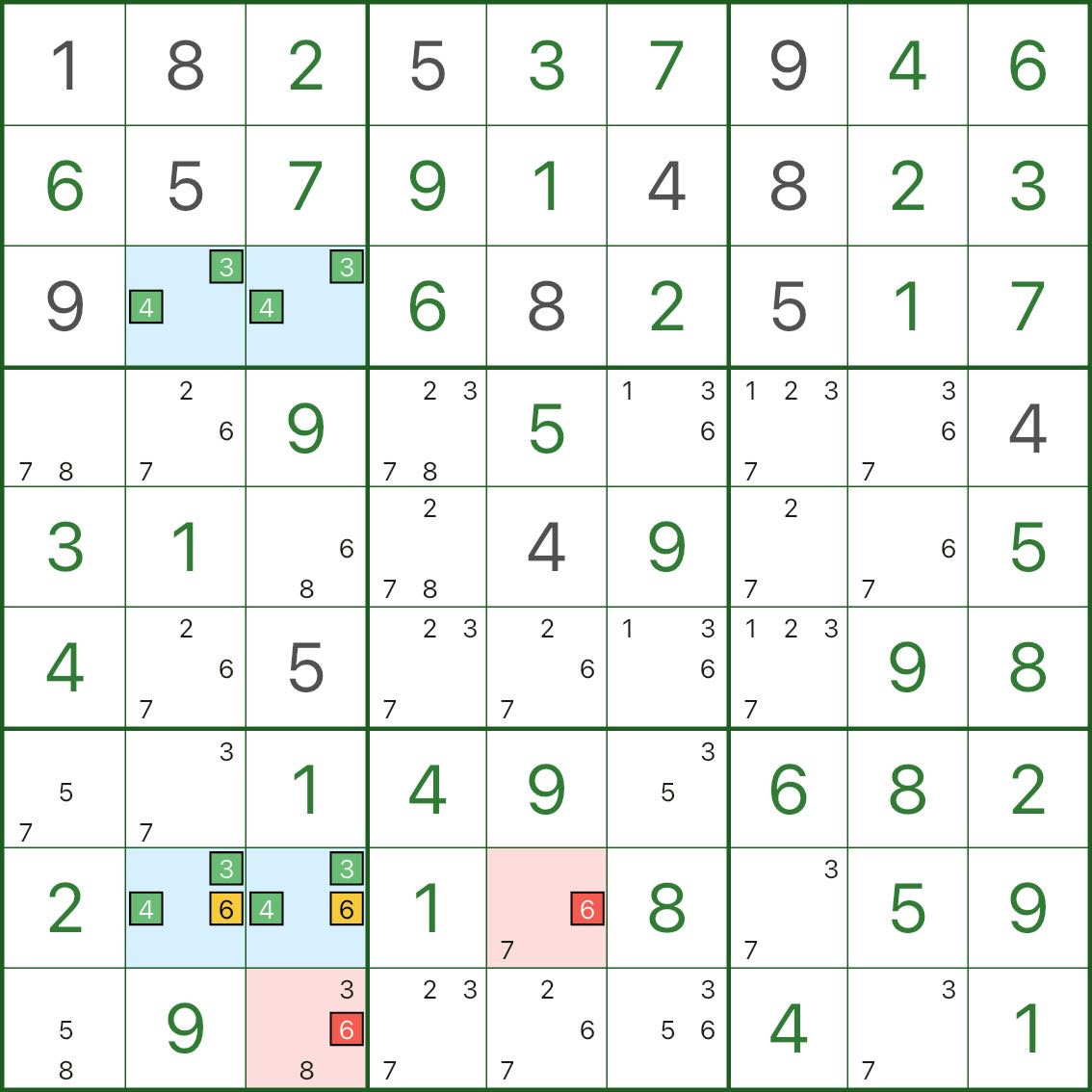
Aquí el rectángulo azul se basa en los candidatos principales 3 y 4.
Dos celdas azules r8c2 y r8c3 también contienen el candidato 6 (por lo que son {3,4,6}).

Ahora considere un candidato rojo 6 (por ejemplo en r8c5 o r9c3) que puede ver ambas celdas del techo:

• si ese 6 rojo fuera cierto, ambos techos serían forzados no 6
• los techos colapsarían de nuevo a {3,4} solamente
• el rectángulo vuelve a convertirse en un patrón mortal {3,4} (rompiendo la unicidad)

Entonces esos 6 candidatos rojos no pueden ser ciertos y pueden ser eliminados.

---

Tipo III: tratar las cubiertas como un “paquete” y formar un subconjunto

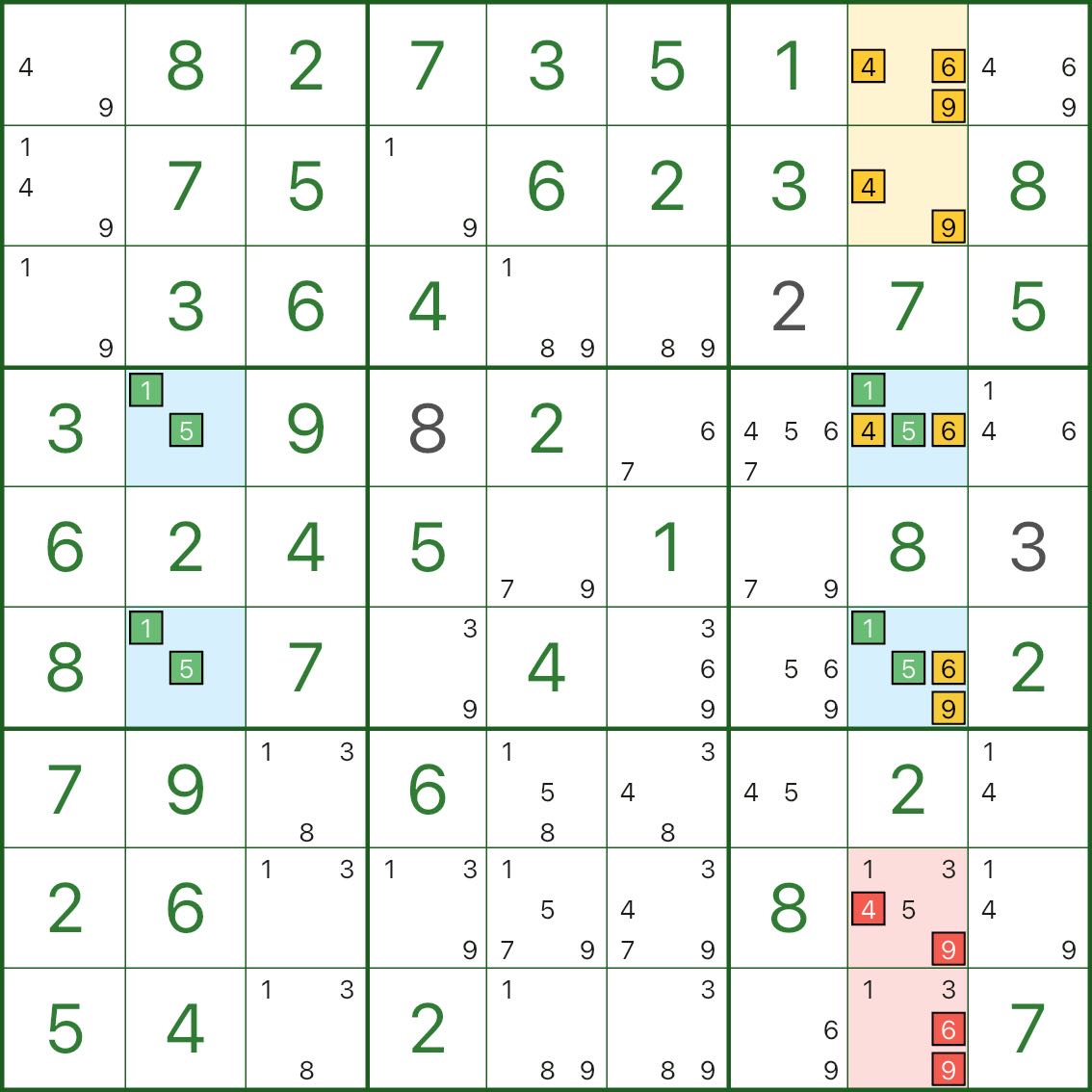
Éste se centra en la columna 8:

• dos celdas azules en la columna 8 contienen candidatos principales 1 y 5
• también comparten dígitos adicionales 4, 6, 9 (por lo que cada uno es {1,5,4,6,9})

La unicidad impone una restricción importante:

• entre esas dos celdas azules, al menos una debe tomar un dígito de {4,6,9}
• de lo contrario, ambos confiarían sólo en {1,5}, convirtiendo el rectángulo en un patrón mortal

Entonces podemos tratar "los dígitos adicionales {4,6,9} de las dos celdas azules" como un paquete.
Junto con las celdas amarillas r1c8 y r2c8, esto efectivamente bloquea los dígitos 4, 6, 9 dentro de un pequeño subconjunto en la columna 8.

Por lo tanto, cualquier otro candidato 4/6/9 en la columna 8 (marcado en rojo) puede ser eliminado.

---

Tipo IV: un par conjugado fuerza un dígito → eliminar el otro

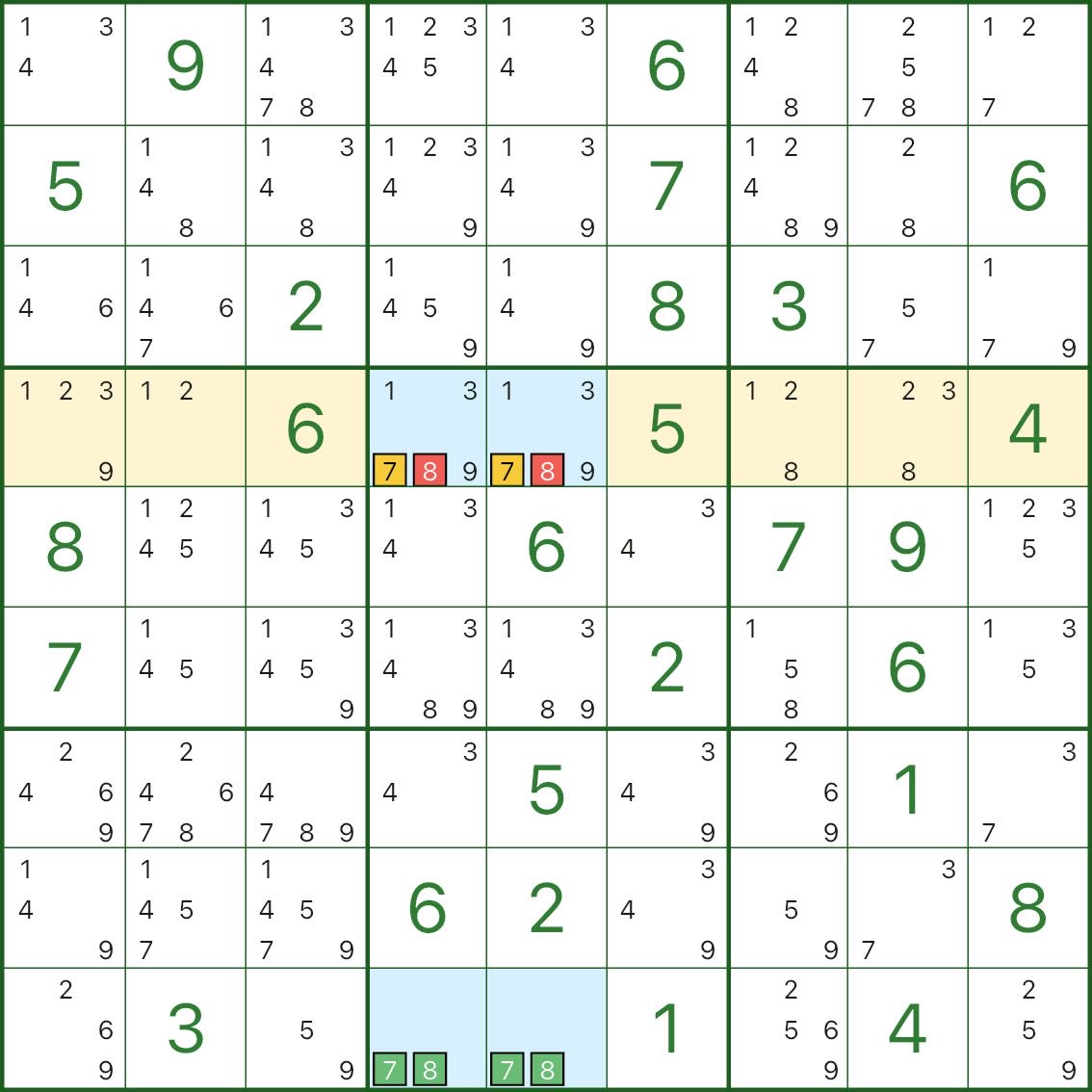
El rectángulo azul está construido nuevamente sobre un par de núcleos (aquí 7 y 8).En fila 4, el candidato 7 aparece solo en las dos celdas azules r4c4 y r4c5.
Eso significa:

• uno de r4c4/r4c5 debe ser 7

Con esta restricción, mantener al candidato 8 en esas mismas celdas azules aún permitiría que el rectángulo colapse en una estructura mortal (rompiendo la unicidad).

Entonces podemos eliminar 8 de r4c4 y r4c5.

---

Tipo V: techos múltiples (2 o 3) → eliminar c que ve todas las celdas del techo

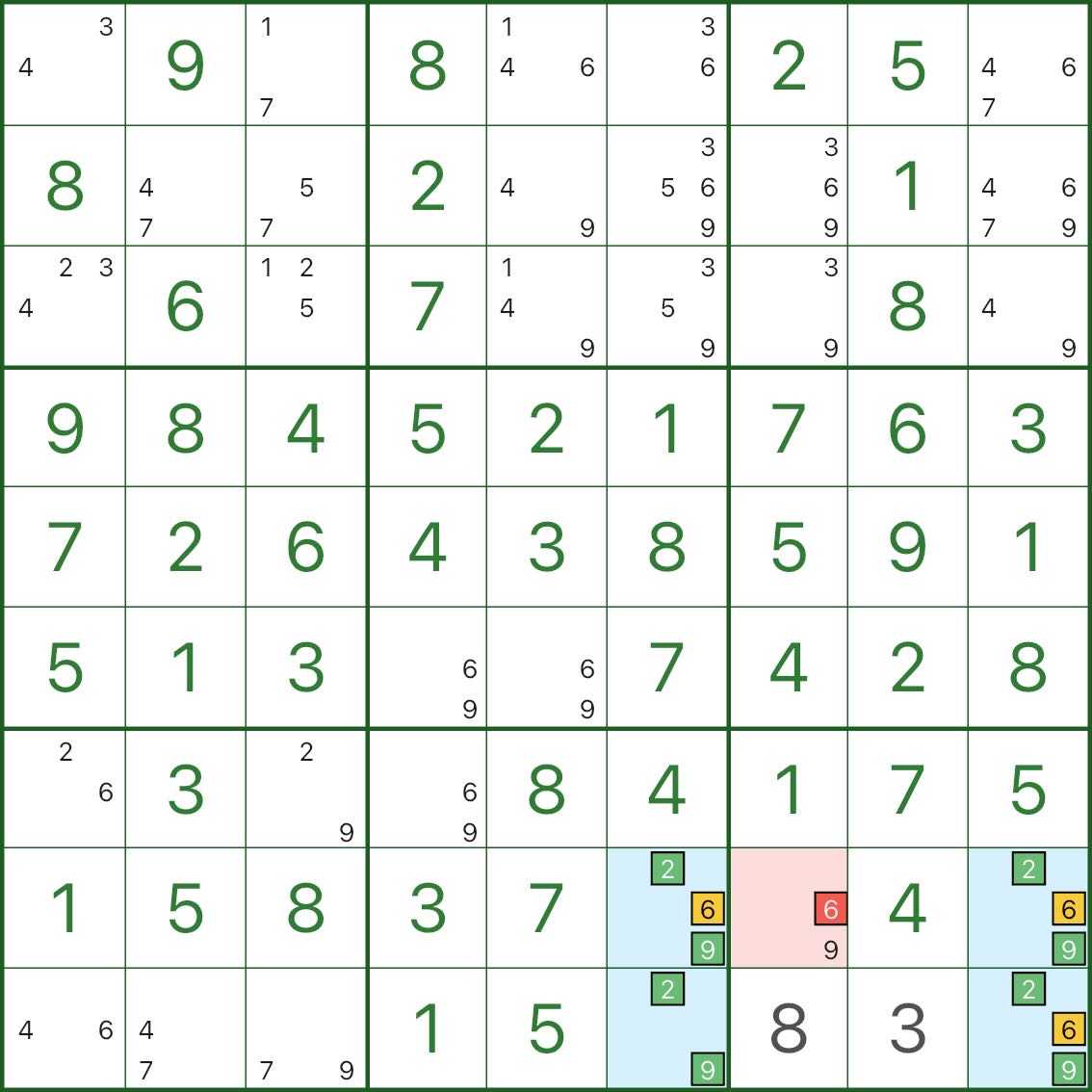
El tipo V no es estrictamente “tres techos”. La idea clave es:

• hay 2 o 3 celdas de techo en el rectángulo y todas comparten el mismo candidato adicional c
• si solo hay 2 celdas del techo, normalmente no comparten la misma fila/columna/caja (si lo hacen, está más cerca del Tipo II)
• si el candidato de una celda c puede ver todas esas celdas del techo, entonces esa c no puede ser verdadera y puede eliminarse

En esta imagen, el rectángulo azul incluye principalmente los dígitos 2, 6, 9:

• tres esquinas azules son {2,6,9}
• la esquina azul restante es {2,9} (faltan 6)

Ahora mire la celda roja r8c7: tiene el candidato 6 y puede ver todas las celdas del techo {2,6,9} en este patrón.

Si r8c7 = 6:

• las tres celdas del techo se verían forzadas a no-6
• colapsarían en {2,9} solamente
• el rectángulo se convierte en un patrón mortal {2,9} (rompiendo la unicidad)

Entonces el candidato 6 en r8c7 no puede ser verdadero y puede eliminarse.

---

3. Ejemplos

Las imágenes 1 a 5 de este artículo ya son ejemplos del Tipo I a V.
Cuando practiques, intenta localizar primero el rectángulo azul y luego haz coincidir las marcas amarillas/rojas con el razonamiento anterior.

---

4. Cómo detectar un rectángulo único

En acertijos reales, puedes buscar en este orden:

1. Busque cuatro celdas vacías que formen un rectángulo de 2×2 (dos filas × dos columnas) y abarquen exactamente dos cuadros
2. Compruebe si las cuatro esquinas comparten los mismos dos candidatos principales (el "par mortal")
3. Luego clasifique según el aspecto de los candidatos adicionales:
   • sólo una esquina tiene candidatos adicionales → Tipo I (a menudo un valor forzado)
   • dos esquinas comparten el mismo dígito adicional c → Tipo II
   • los dígitos adicionales de los techos pueden formar un subconjunto en una fila/columna/cuadro → Tipo III
   • en una casa, un dígito central aparece sólo en dos celdas rectangulares → Tipo IV
   • dos o tres esquinas comparten el mismo dígito adicional c (para 2 techos, normalmente no comparten una casa) → Tipo V

Eso es UR en una frase: nunca permitas que el rectángulo colapse en un patrón mortal; de lo contrario, se rompería la unicidad.