Pares y subconjuntos

Pares y subconjuntos desnudos/ocultos

Los pares y subconjuntos son algunas de las técnicas de “eliminación de candidatos” más útiles. Tienen diferentes nombres, pero todos hacen lo mismo:

En una casa (una fila/columna/cuadro), un pequeño conjunto de celdas y un pequeño conjunto de dígitos "reservan los espacios" entre sí, de modo que esos dígitos no puedan aparecer en ninguna otra parte de esa casa.

No es necesario memorizar la jerga. Una simple regla general:

• Desnudo: comienza desde lo que muestran las celdas (estas celdas contienen solo estos dígitos)
• Oculto: comienza desde donde puede ir un dígito (estos dígitos solo pueden ir en estas celdas)

---

1. Pareja desnuda

En la misma casa, si dos celdas contienen sólo los mismos dos candidatos (por ejemplo, {a,b}), tienes un par desnudo.

Eso significa:

• Una celda debe ser a, la otra debe ser b (orden desconocido)
• Entonces los candidatos a y b pueden eliminarse de cada dos celdas vacías en esa casa

Primero, mire la imagen a continuación: céntrese en el Cuadro 3 resaltado y las dos celdas verdes r2c9 y r3c9.
Notarás que solo pueden ser {1,5}.

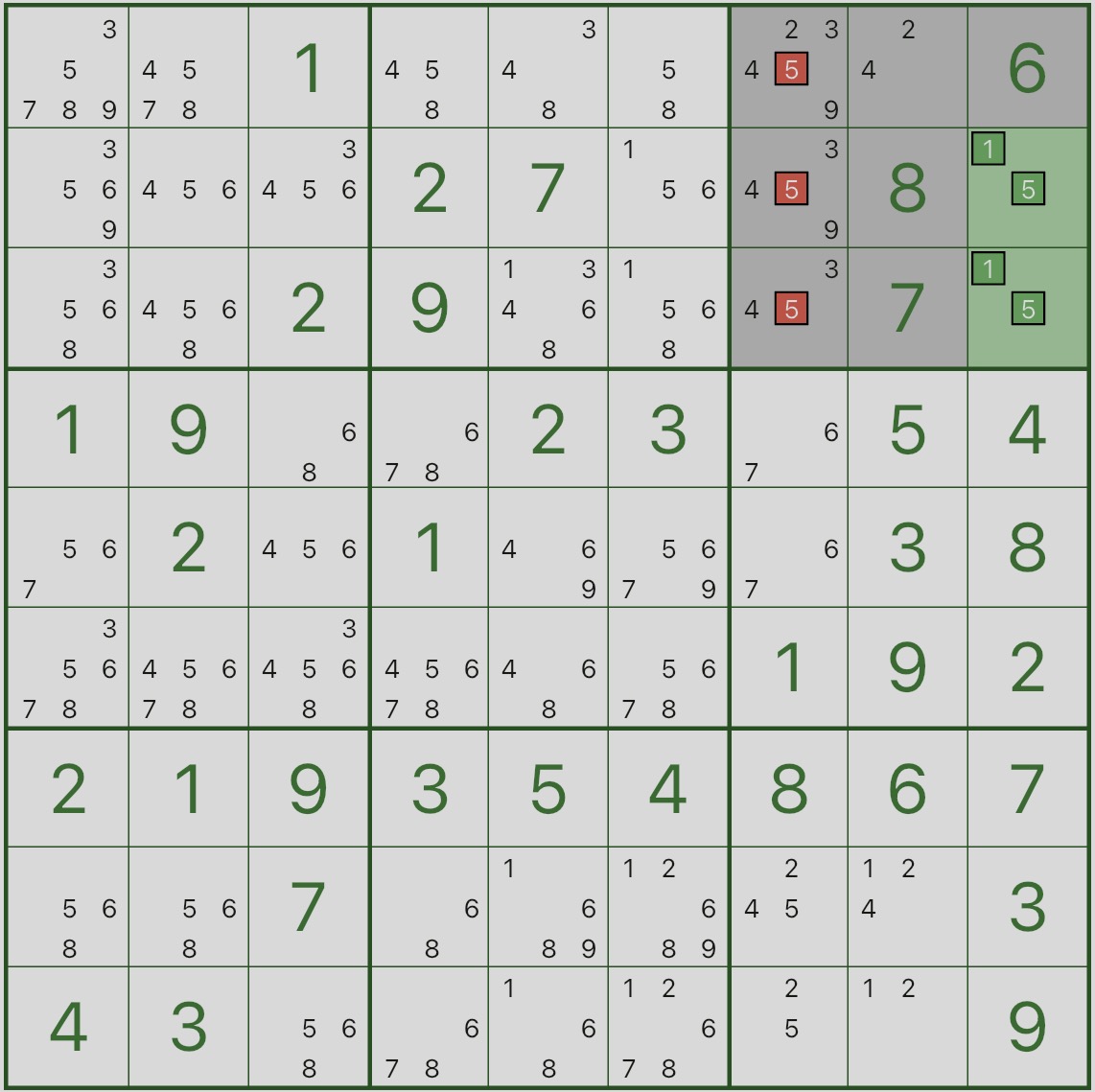
Esto significa: en el Cuadro 3, los dígitos 1 y 5 están “reservados” para r2c9 y r3c9.

Ahora mire los candidatos rojos: el candidato 5 en r1c7, r2c7, r3c7 se puede eliminar.

Una prueba rápida por contradicción:

• Supongamos que r1c7 es 5 (la misma lógica se aplica a r2c7 y r3c7)
• Entonces el Cuadro 3 ya contiene un 5, por lo que r2c9 y r3c9 no pueden ser 5 y están obligados a ser 1.
• Pero r2c9 y r3c9 comparten la misma columna (columna 9), por lo que no pueden ser ambos 1 - contradicción
  ⇒ esos 5 candidatos rojos son imposibles y pueden eliminarse

---

2. Par oculto

En la misma casa, si el candidato a aparece exactamente en dos celdas y el candidato b también aparece en las mismas dos celdas, tienes un par oculto.

Esas dos celdas pueden mostrar candidatos adicionales, pero a y b ya están bloqueados para ellos, por lo que puedes:

• Elimina todos los candidatos excepto a y b de esas dos celdas

Primero, mire la imagen a continuación: céntrese en la columna resaltada 4.
Encuentre dónde aparecen los candidatos 4 y 5 en esa columna; verá que aparecen solo en r1c4 y r6c4.

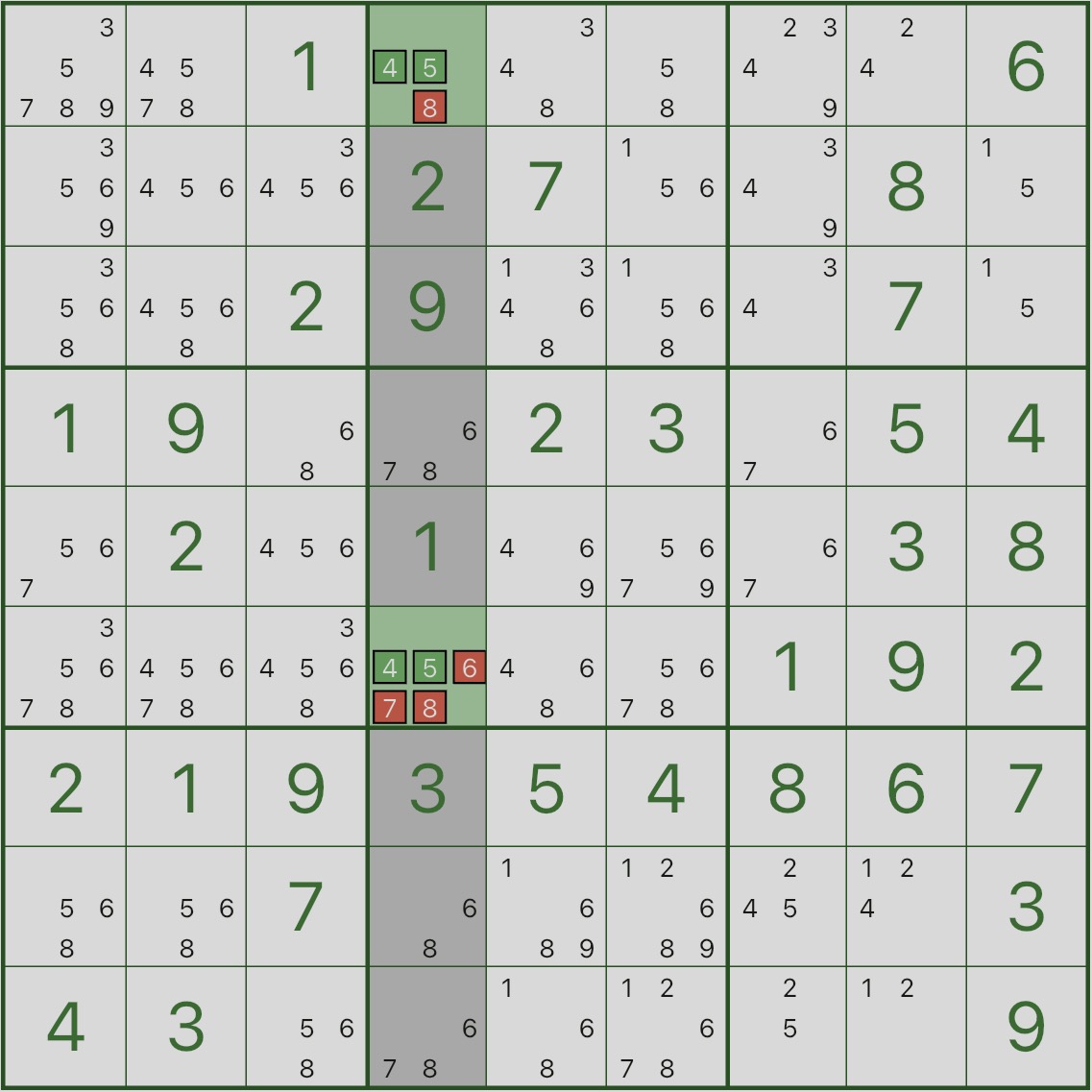
Esto significa: en la columna 4, los dígitos 4 y 5 deben colocarse en r1c4 y r6c4.

¿Por qué podemos eliminar otros candidatos de r1c4 y r6c4?

• Supongamos que r1c4 toma un dígito que no es 4 o 5
• Entonces tanto 4 como 5 tendrían que encajar sólo en r6c4
• Una sola celda no puede tener al mismo tiempo 4 y 5 - contradicción
  ⇒ r1c4 y r6c4 deben ser {4,5}, por lo que se pueden eliminar otros candidatos en esas celdas

---

3. Subconjunto desnudo (triple / cuádruple)

Esta es la idea de la “pareja desnuda”, generalizada:

Si N celdas en una casa contienen colectivamente solo N dígitos (por ejemplo, tres celdas contienen solo {a,b,c}), tienes un triple desnudo. La misma idea se aplica a los quads.

Esos dígitos deben colocarse dentro de esas N celdas, entonces:

• Elimina esos dígitos (por ejemplo, a, b, c) de cada dos celdas vacías de esa casa.

Primero, mire la imagen a continuación: céntrese en la fila 8 resaltada y las tres celdas r8c1, r8c2, r8c4.
Notarás que estas tres celdas en conjunto contienen solo {5,6,8}.

Esto significa: en la fila 8, los dígitos 5, 6, 8 deben colocarse dentro de r8c1, r8c2, r8c4.

Es por eso que los candidatos rojos 5, 6, 8 en el resto de la fila 8 se pueden eliminar.

Una visión de contradicción simple:

• Si otra celda en la fila 8 “toma” uno de {5,6,8}
• Entonces esas tres celdas tendrían que llenarse usando solo dos dígitos para tres celdas
• Eso no puede funcionar - contradicción

---

4. Subconjunto oculto (triple/cuádruple)

Esta es la idea del “par oculto”, generalizada:

Si N dígitos en una casa aparecen solo en las mismas N celdas (incluso si esas celdas contienen candidatos adicionales), tienes un triple/quad oculto.

Esos N dígitos están bloqueados en esas N celdas, entonces:

• Elimina todos los candidatos excepto esos N dígitos de esas celdas

Primero, mire la imagen a continuación: céntrese en la columna resaltada 5.
Notarás que los dígitos 4,7,8 aparecen solo en r1c5, r8c5, r9c5.

Esto significa: en la columna 5, los dígitos 4, 7, 8 deben colocarse dentro de r1c5, r8c5, r9c5.

Por tanto, en estas tres celdas podemos eliminar cualquier otro candidato que no sea 4, 7 u 8.

¿Por qué es eso seguro?

• Si alguna de estas celdas tomó un dígito diferente
• Entonces 4, 7 y 8 tendrían menos de tres lugares para encajar: contradicción

---

5. Consejos para detectarlos más rápido

• Mantenga a los candidatos razonablemente completos (los necesitará para acertijos más difíciles)
• Busque primero patrones desnudos: comience desde celdas con muy pocos candidatos (2, 3 o 4)
• Luego busque patrones ocultos: en una casa, verifique si un dígito está limitado a 2, 3 o 4 puntos
• Después de las eliminaciones, haga una pausa y vuelva a mirar: los candidatos simplificados a menudo revelan el siguiente paso