Guías / Conceptos básicos de la cadena
Conceptos básicos de la cadena
> Vínculos fuertes / vínculos débiles / alternancia (AIC)
Advanced
Conceptos básicos de la cadena
Vínculos fuertes / vínculos débiles / alternancia (AIC)
Las cadenas son un componente básico de muchas técnicas avanzadas de Sudoku.
En el fondo, una cadena es solo una secuencia de implicaciones “si… entonces…” que permite que las deducciones viajen a través de la red.
Después de este capítulo, las sugerencias avanzadas como cadenas de un solo dígito, cometa, rascacielos, medusa y AIC serán mucho más legibles.
Usamos r1c1 para referirnos a la posición de una celda:
r = fila, c = columna.
Para que los diagramas sean más fáciles de seguir, utilizamos:
- Línea continua verde: vínculo fuerte
- Línea discontinua amarilla: eslabón débil
- Antecedentes del candidato azul/amarillo: dos “estados” mutuamente excluyentes, para visualizar la alternancia
- Candidato rojo: el candidato a eliminar en este paso
Recordatorio: una cadena es bidireccional. Las flechas son sólo para facilitar la lectura.
¿Qué es una cadena?
En resumen, una cadena conecta las relaciones de los candidatos para que pueda seguir aplicando la lógica de "si... entonces...":
Si A no es posible, entonces B debe ser verdadero;
si B es verdadero, entonces C debe ser falso;
…
Una cadena está hecha de:
- Nodos: candidatos (un dígito candidato en una celda)
- Vínculos: relaciones entre candidatos (fuertes/débiles)
Una cadena no significa necesariamente "siempre eliminamos el inicio". Es más como un camino de razonamiento:
- Llegar a una contradicción ⇒ demostrar que un candidato no puede ser cierto → eliminarlo
- Alcanzar una verdad forzada ⇒ demostrar que un candidato debe ser verdadero → colocar un valor
Este artículo se centra en las “cadenas de un solo dígito” más comunes: razonamiento sobre candidatos de un dígito d.
(Las relaciones entre células bivalor y los fuertes vínculos agrupados/regionales se tratan más adelante).
Vínculos fuertes y vínculos débiles
Vínculo fuerte (par conjugado)
Mnemónico: esto o lo otro.
En la misma unidad (fila/columna/cuadro), si aparece un dígito d en exactamente dos celdas candidatas, esos dos candidatos forman un vínculo fuerte (un par conjugado).
La implicación clave es “NO obliga a SÍ”:
- Si NO es A, entonces B (Si A no es d, entonces B debe ser d)
- Si NO es B, entonces A
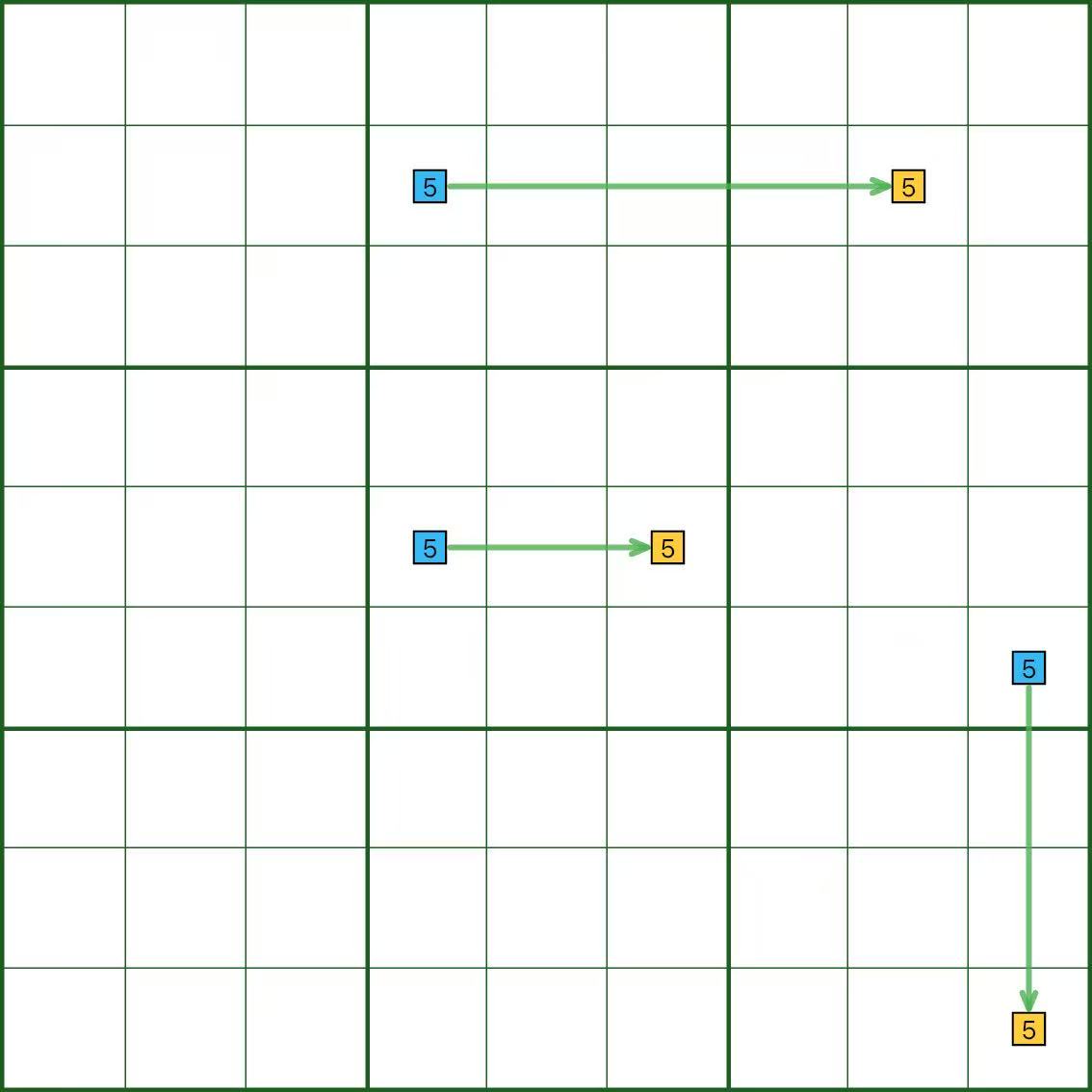
En el diagrama, el dígito 5 forma vínculos fuertes en una fila, una columna y un cuadro.
Puedes leerlo desde cualquier extremo; Las flechas son sólo una ayuda para la lectura.
Nota importante: todo vínculo fuerte es también un vínculo débil.
Dado que los dos candidatos comparten la misma unidad, no pueden ser ambos verdaderos:
- Si A, entonces NO B (Si A es d, entonces B no es d)
Resumen de una línea:
Vínculo fuerte = exclusividad débil + “uno de ellos debe ser verdadero”
enlace débil
Mnemónico: si se ven, ambos no pueden ser sinceros.
Un eslabón débil expresa una cosa:
Dos candidatos no pueden ser ambos verdaderos.
En las cadenas de un solo dígito, el eslabón débil más común son dos candidatos del mismo dígito d en la misma unidad.
Implicación:
- Si A, entonces NO B
Pero no al revés:
- Si A es falso, no se puede concluir B (puede haber un tercer punto).
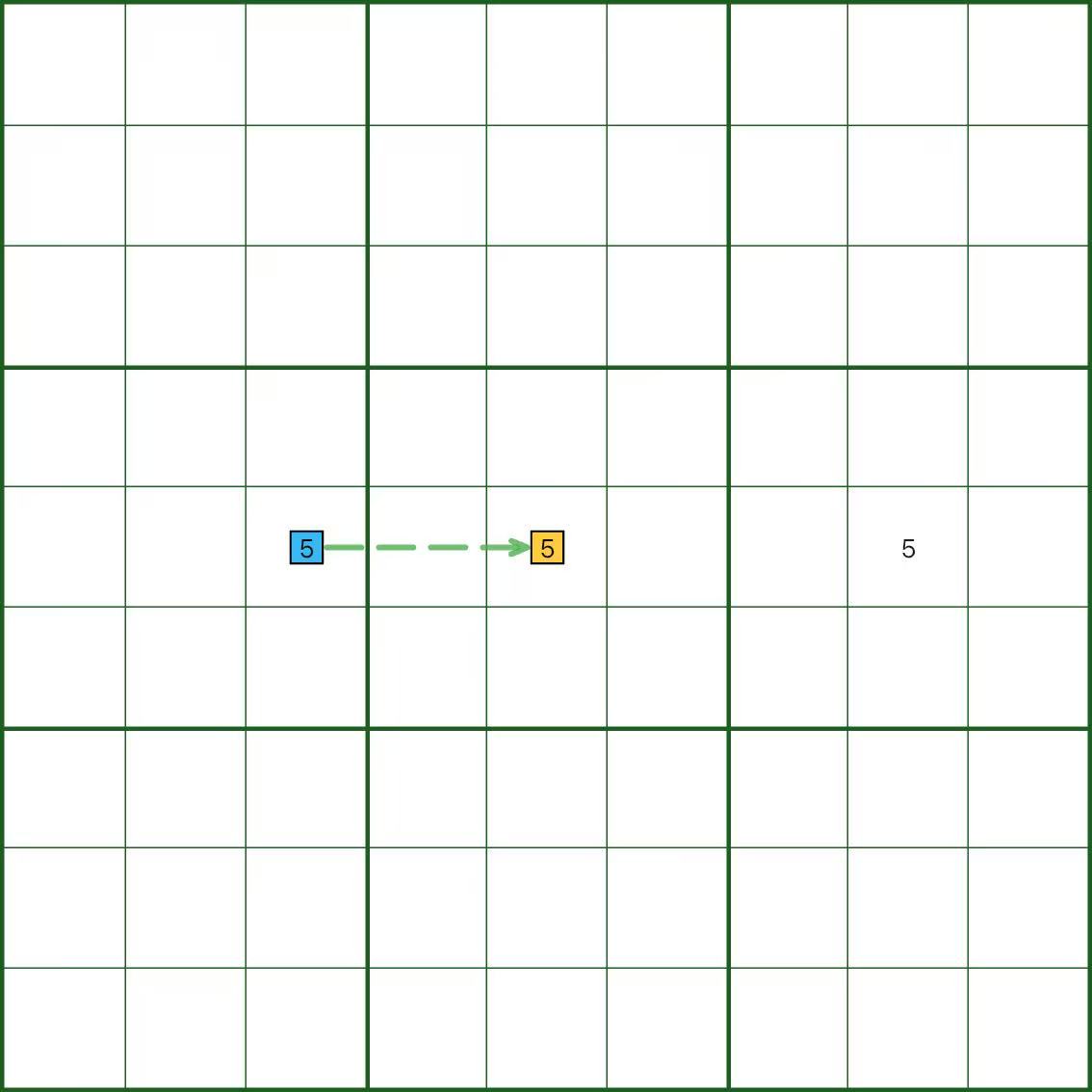
En el diagrama, el dígito 5 tiene tres celdas candidatas seguidas, por lo que cada par está débilmente vinculado.
La imagen muestra solo un segmento discontinuo solo para mostrar cómo se ve un eslabón débil.
¿Cómo funcionan las cadenas?
Para propagarse a lo largo de una cadena, recuerde dos reglas:
- Verdadero → (débil) → Falso
Los vínculos débiles son excluyentes: si A es verdadero, B debe ser falso. - Falso → (fuerte) → Verdadero
Los vínculos fuertes son uno u otro: si A es falso, el otro candidato debe ser verdadero.
Entonces, una cadena de trabajo normalmente alterna:
Falso —(fuerte)→ Verdadero —(débil)→ Falso —(fuerte)→ Verdadero —(débil)→ Falso …
¿Por qué alternar?
- rupturas débil-débil: "falso" no se propaga a través de un enlace débil
- fuerte-fuerte puede conectarse, pero en muchos acertijos a menudo corresponde a patrones más simples, por lo que las cadenas son más útiles para la propagación alterna.
Ejemplo
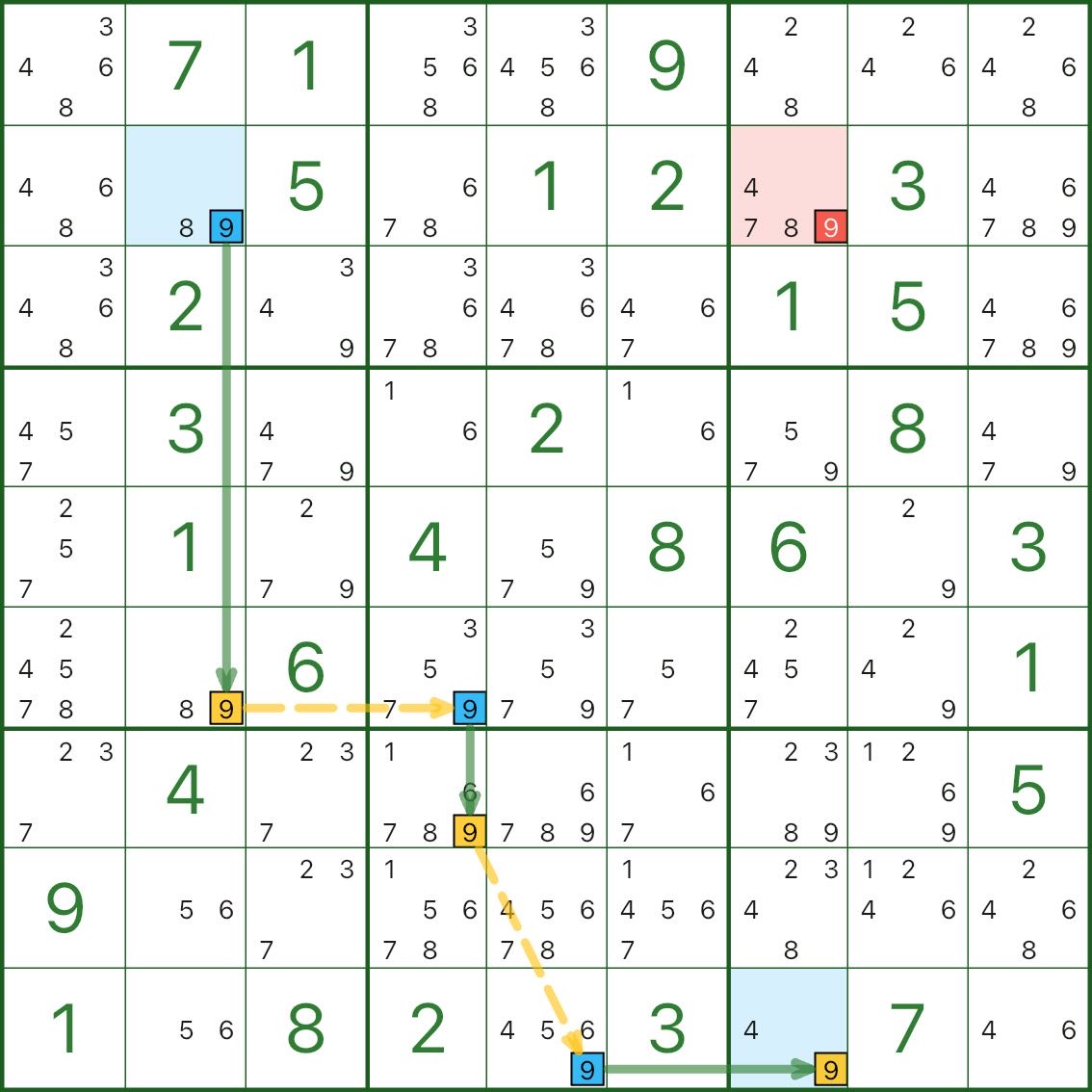
En el diagrama, el candidato rojo es el dígito 9 en r2c7.
Léelo así:
Desde el inicio resaltado: una vez que r2c2 NO es 9, la cadena se propaga para forzar r9c7 = 9
(puedes ver la alternancia limpia False → True → False → True → False → True)Ahora use una contradicción: suponga que el candidato rojo r2c7 = 9 es verdadero
- r2c7 ve r2c2 en la misma fila, por lo que r2c2 no puede ser 9 (r2c2(9) es falso)
- propagar ese "falso" a través de la cadena, obligando a r9c7(9) a ser verdadero
- r2c7 y r9c7 están en la misma columna, por lo que no pueden ser ambos 9 → contradicción
Por lo tanto, r2c7 no puede ser 9 y ese candidato rojo puede ser eliminado.
Práctica
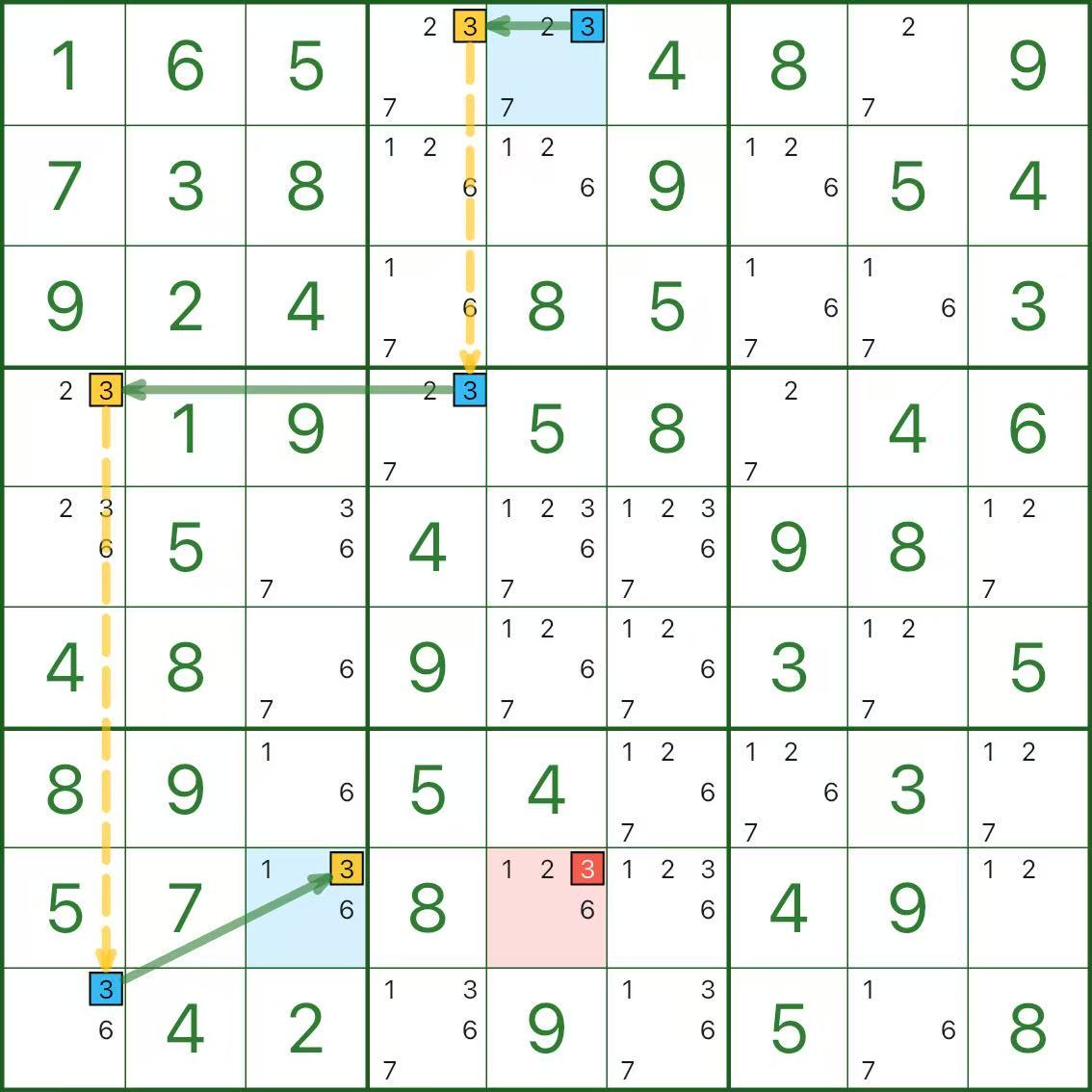
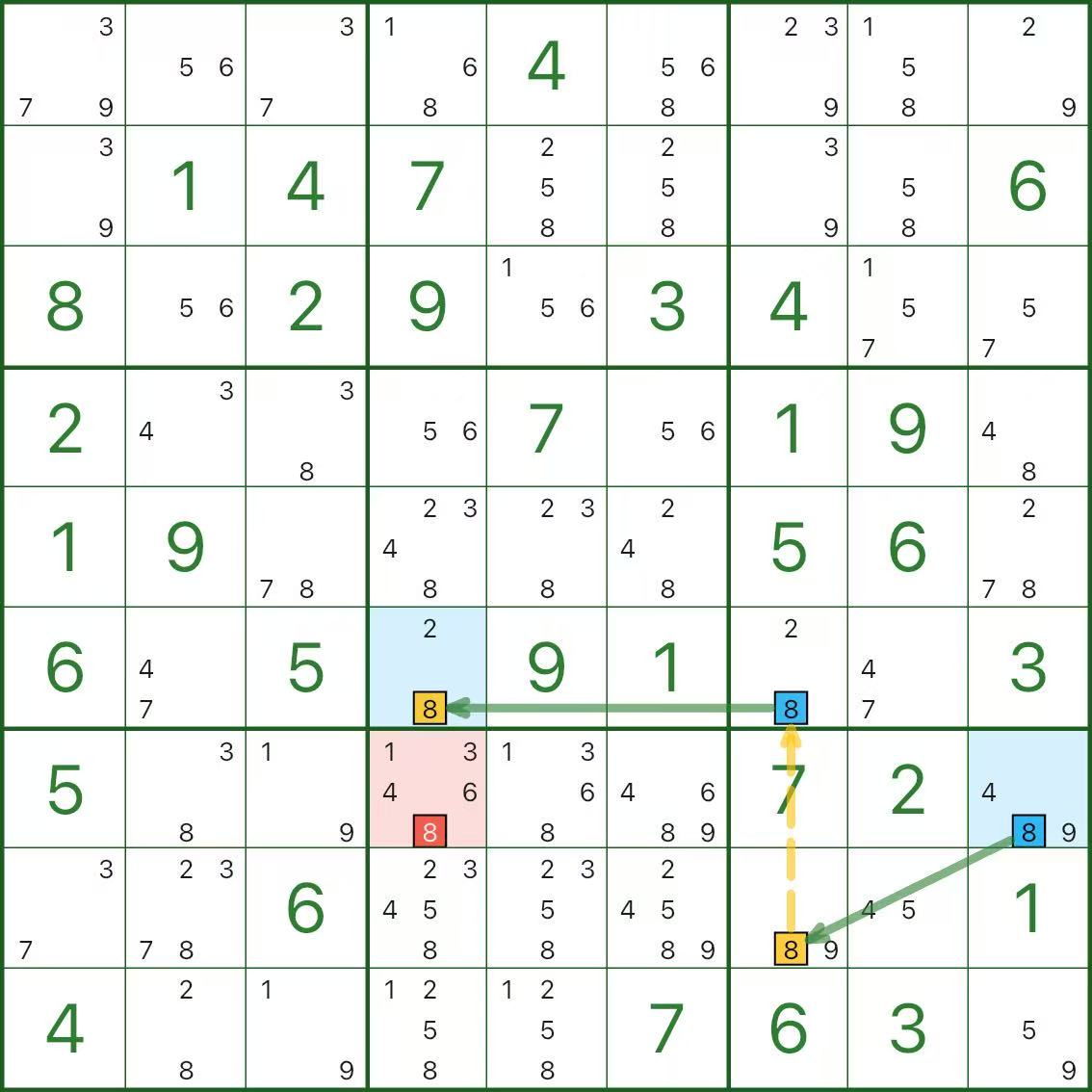
Los siguientes tres diagramas son todos cadenas de un solo dígito. Tome su tiempo.
Tres preguntas rápidas de autoevaluación:
- ¿Qué segmentos son vínculos fuertes y por qué son “esto o lo otro”?
- ¿Qué segmentos son eslabones débiles y por qué se excluyen mutuamente?
- ¿Por qué el candidato rojo conduce a una contradicción?
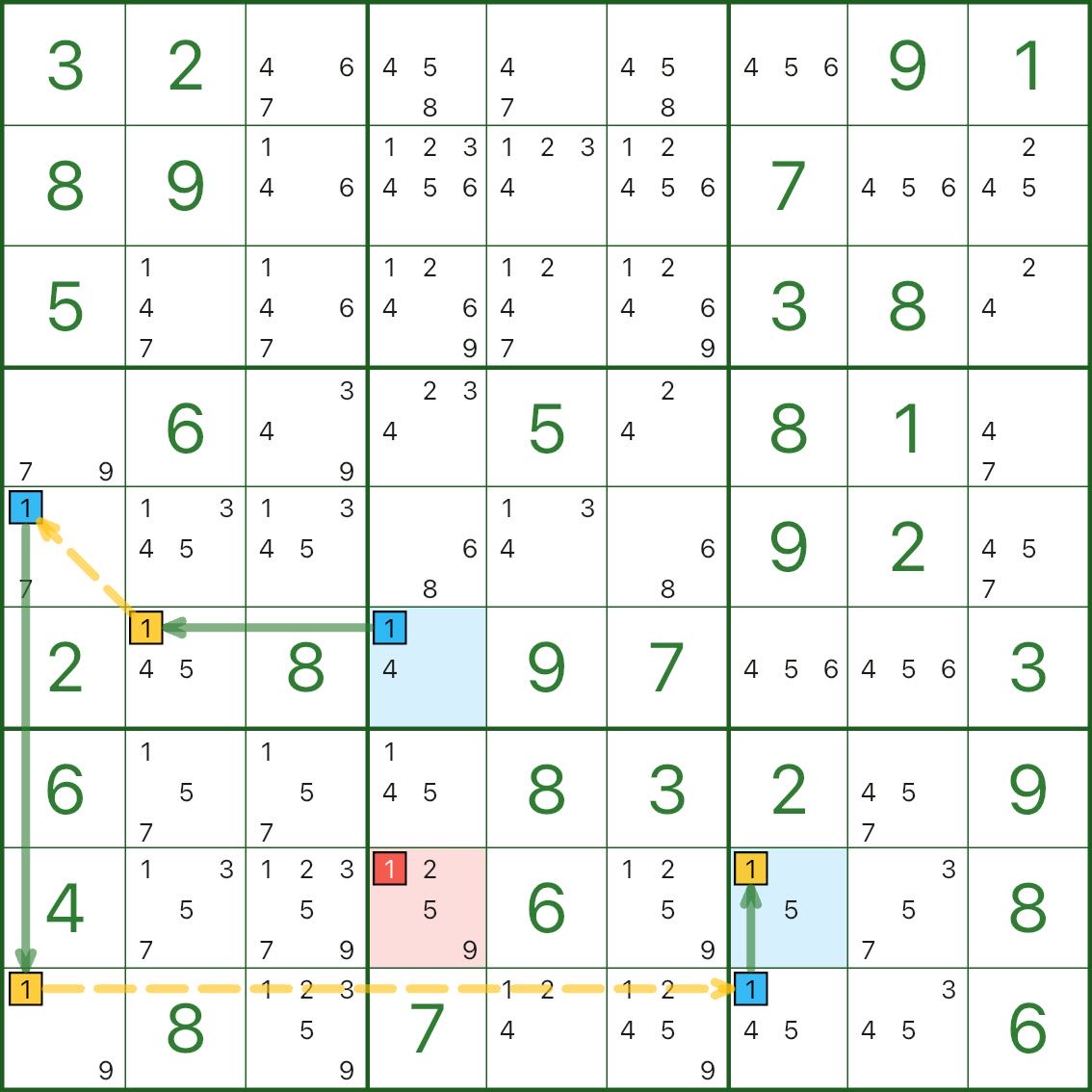
Si al principio se siente un poco retorcido, es completamente normal.
Eso es una cadena: la base de muchas técnicas avanzadas; siéntete cómodo con ella antes de seguir adelante.