XY-Wing

Description

XY-Wing (also known as Y-Wing) is a short candidate elimination chain made of one pivot and two wings.

Its shape looks like this:

• Pivot (blue): exactly two candidates x, y
• Wings (yellow): {x, z} and {y, z}

Conclusion: any cell that can see both wings cannot contain z, so candidate z can be eliminated there.

---

Explanation

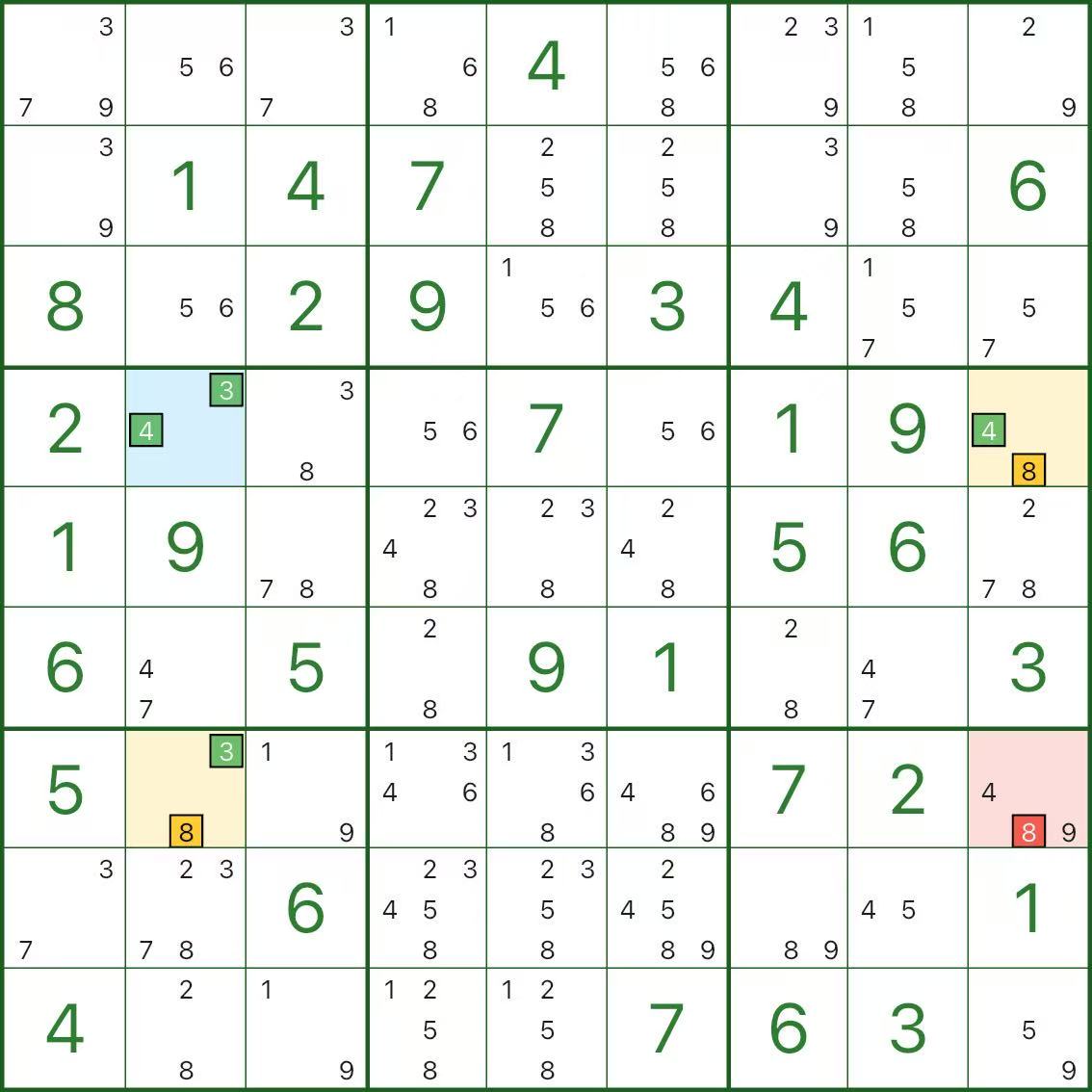
In the image above, we want to eliminate candidate 8 in r7c9 (red).
The blue pivot is r4c2, with candidates 3 and 4.
The two yellow wings are:

• r4c9: candidates 4 and 8
• r7c2: candidates 3 and 8

Why can we remove 8 from r7c9? A short contradiction is enough:

• Assume r7c9 = 8 (the red candidate is true)
• r7c9 can see both wings, so 8 is eliminated from both wings:
  • r4c9 must be 4
  • r7c2 must be 3
• Now the pivot r4c2 is stuck:
  • r4c9 = 4 ⇒ r4c2 cannot be 4 (same row)
  • r7c2 = 3 ⇒ r4c2 cannot be 3 (same column)
  • r4c2 only had {3,4} ⇒ no value fits (contradiction)

So the assumption is impossible: r7c9 cannot be 8, and candidate 8 can be eliminated.

---

Examples

These images show more XY-Wing patterns. Try to spot the same structure: pivot (blue) / two wings (yellow) / elimination (red).

---

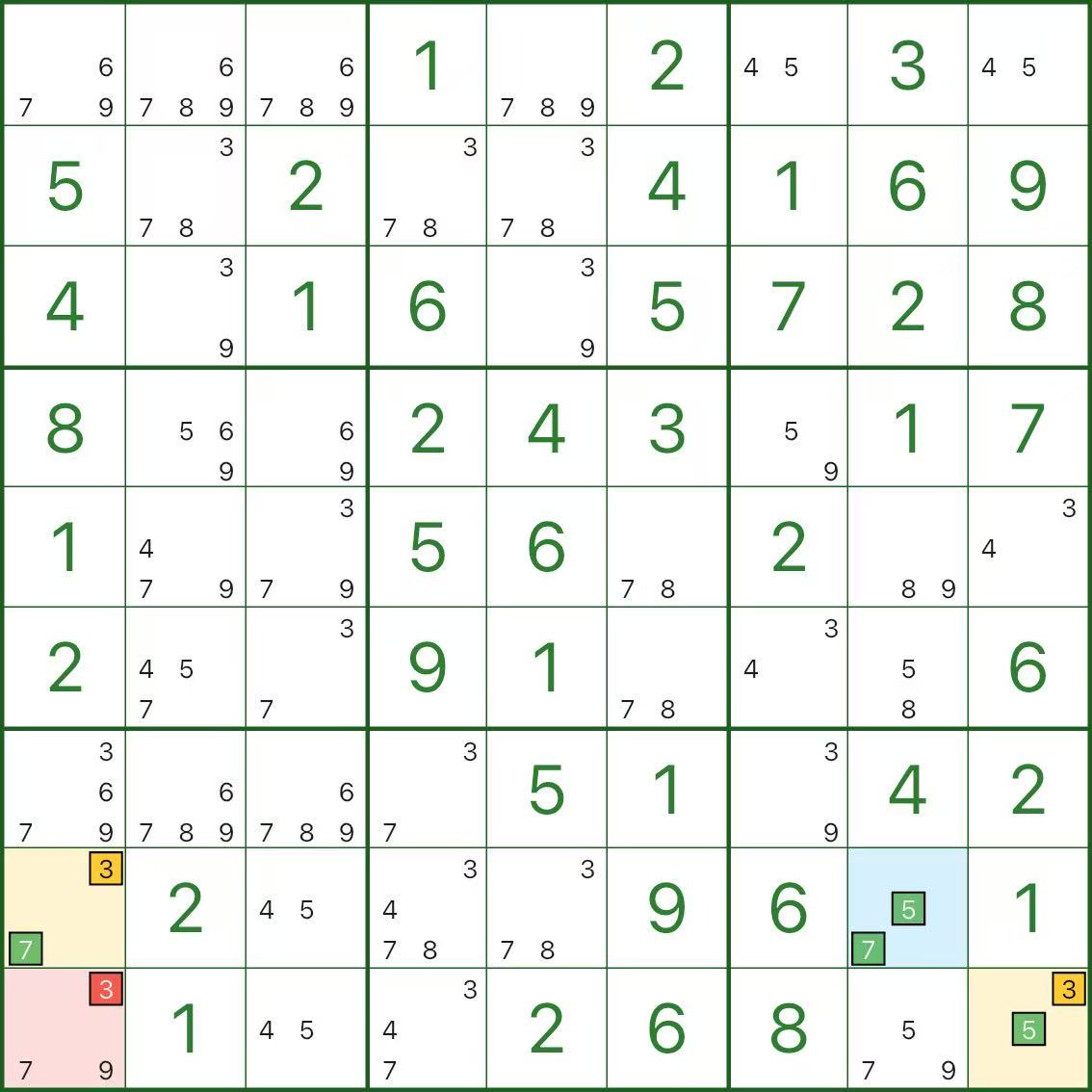
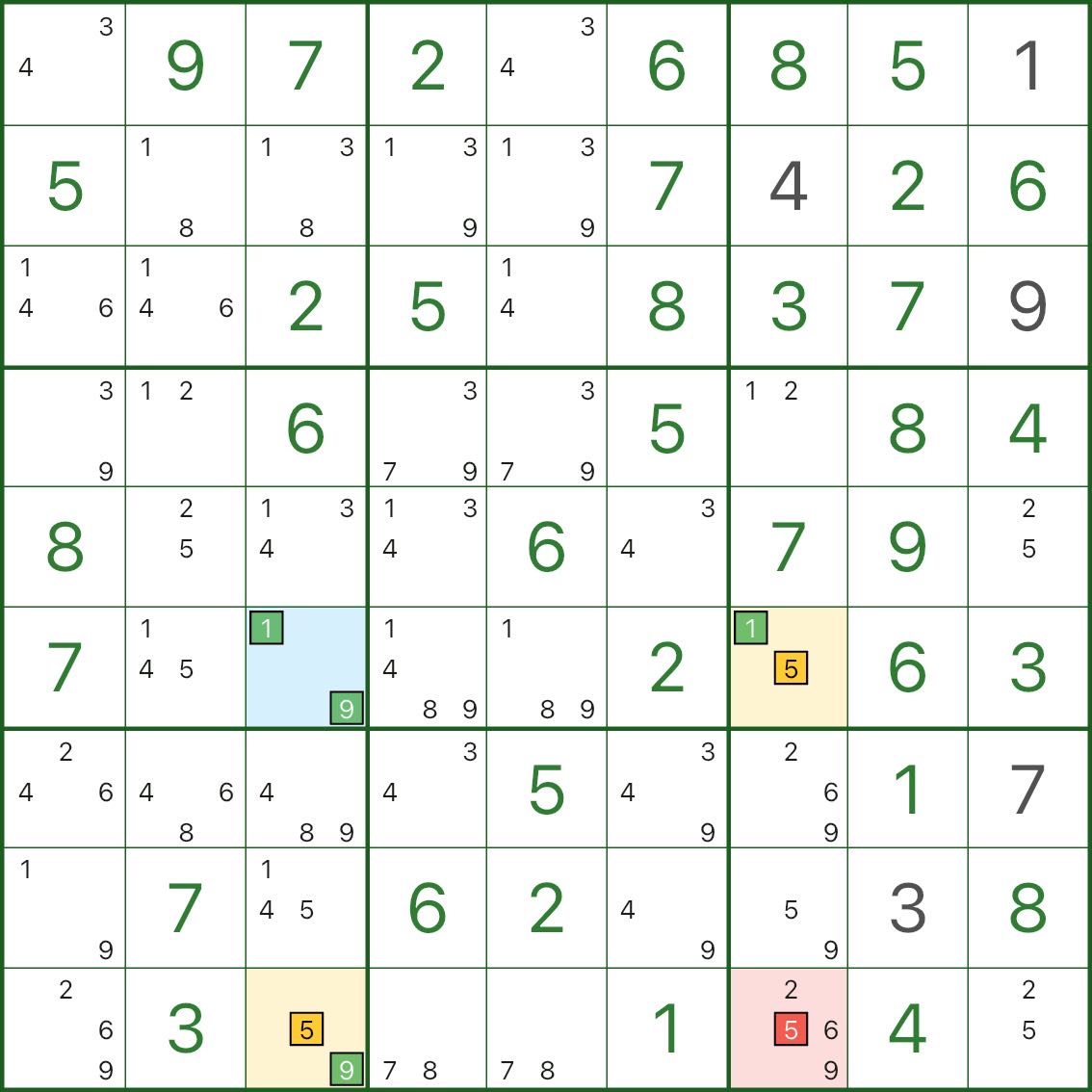
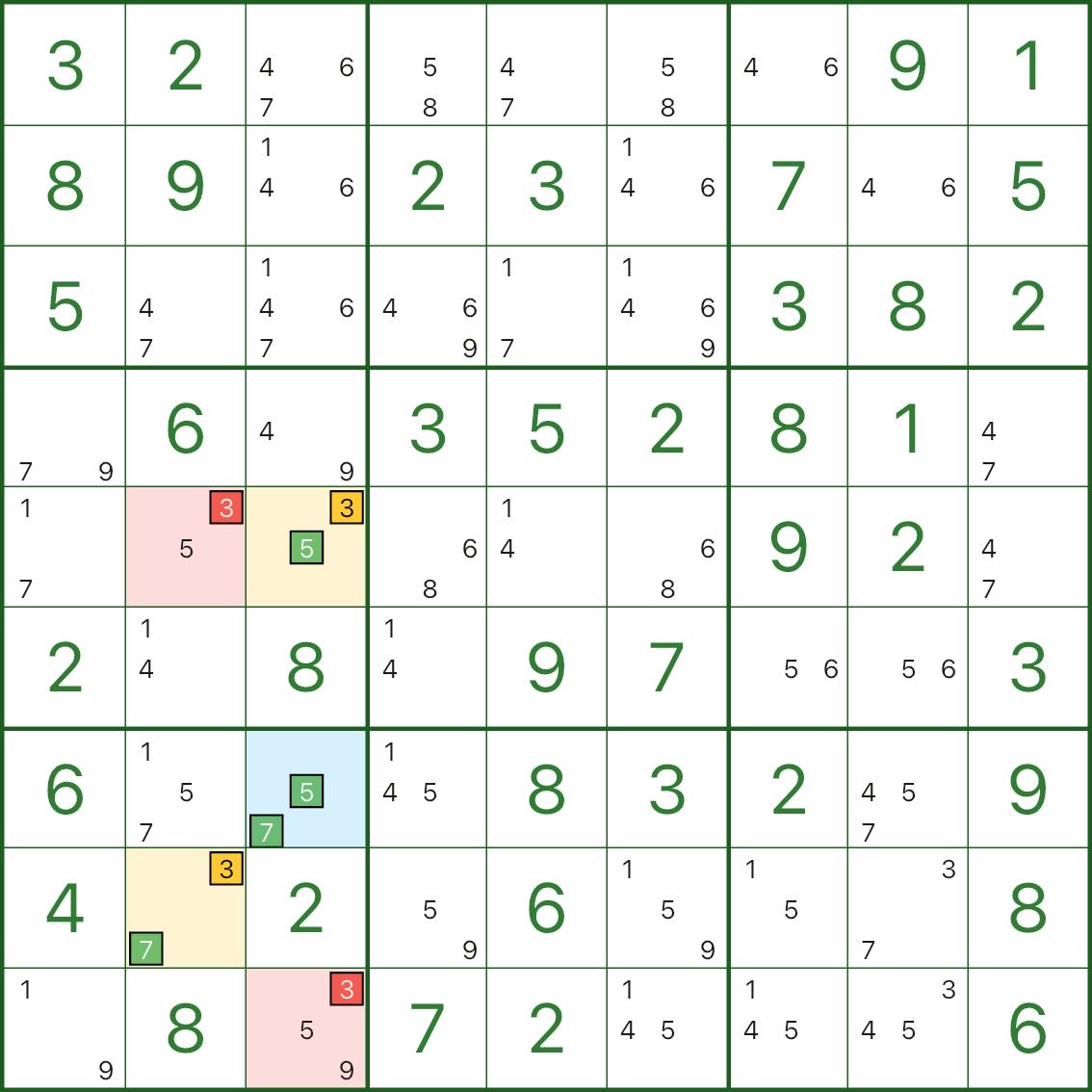
How to Find XY-Wing

One-line checklist: find a two-candidate pivot {x,y}, find two two-candidate wings {x,z} and {y,z}, then eliminate z from any cell that sees both wings.

In a real puzzle:

1. Find a cell with exactly two candidates as the pivot (blue)
2. Find two cells that can see the pivot, each with exactly two candidates, shaped like {x,z} and {y,z} (yellow)
3. Any cell that can see both wings is a typical elimination spot: remove candidate z there (red)