XYZ-Wing

Description

XYZ-Wing is similar to XY-Wing: both use a “pivot + two wings” pattern to eliminate a shared candidate by contradiction.
The key difference is that the pivot has three candidates in XYZ-Wing, so the elimination cell typically needs to see the pivot and both wings (because the shared candidate could also be placed in the pivot).

The structure looks like this (focus on the shared candidate z):

• Pivot (blue): candidates x, y, z
• Wings (yellow): {x, z} and {y, z}

Conclusion: in any cell that can see the pivot and both wings, candidate z can be eliminated.

---

Explanation

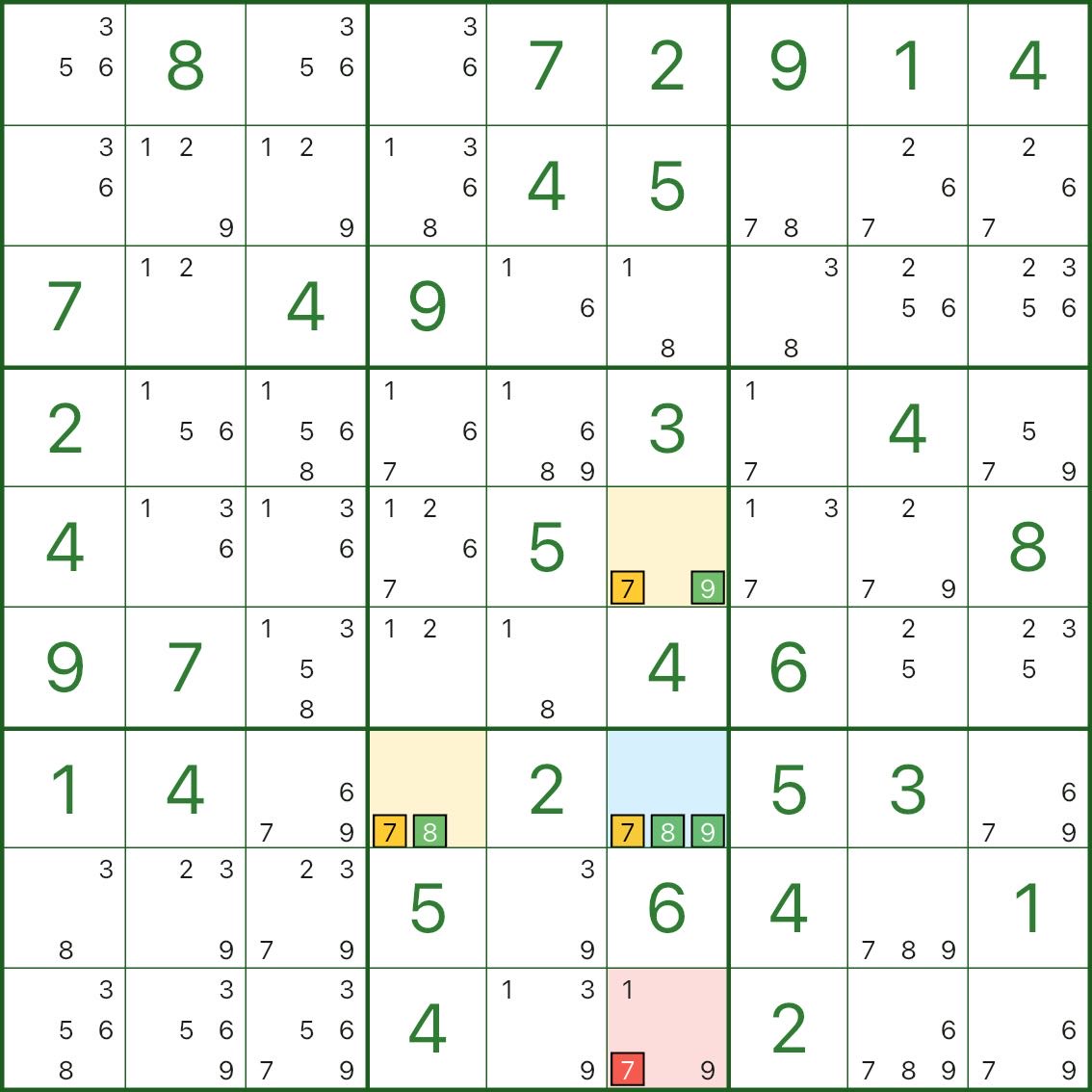
In the image above, we want to eliminate candidate 7 in r9c6 (red).
The blue pivot is r7c6, with candidates 7, 8, 9.
The two yellow wings are:

• r5c6: candidates 7 and 9
• r7c4: candidates 7 and 8

Why can we remove 7 from r9c6? A short contradiction is enough:

• Assume r9c6 = 7 (the red candidate is true)
• r9c6 can see both wings, so 7 is removed from both wings:
  • r5c6 must be 9
  • r7c4 must be 8
• Now the pivot r7c6 has no value left:
  • r9c6 = 7 ⇒ r7c6 cannot be 7 (same column)
  • r5c6 = 9 ⇒ r7c6 cannot be 9 (same column)
  • r7c4 = 8 ⇒ r7c6 cannot be 8 (same row)
  • r7c6 only had {7,8,9} ⇒ no value fits (contradiction)

So the assumption is impossible: r9c6 cannot be 7, and candidate 7 can be eliminated.

---

Examples

These images show more XYZ-Wing patterns. Try to spot the same structure: pivot (blue) / two wings (yellow) / elimination (red).

---

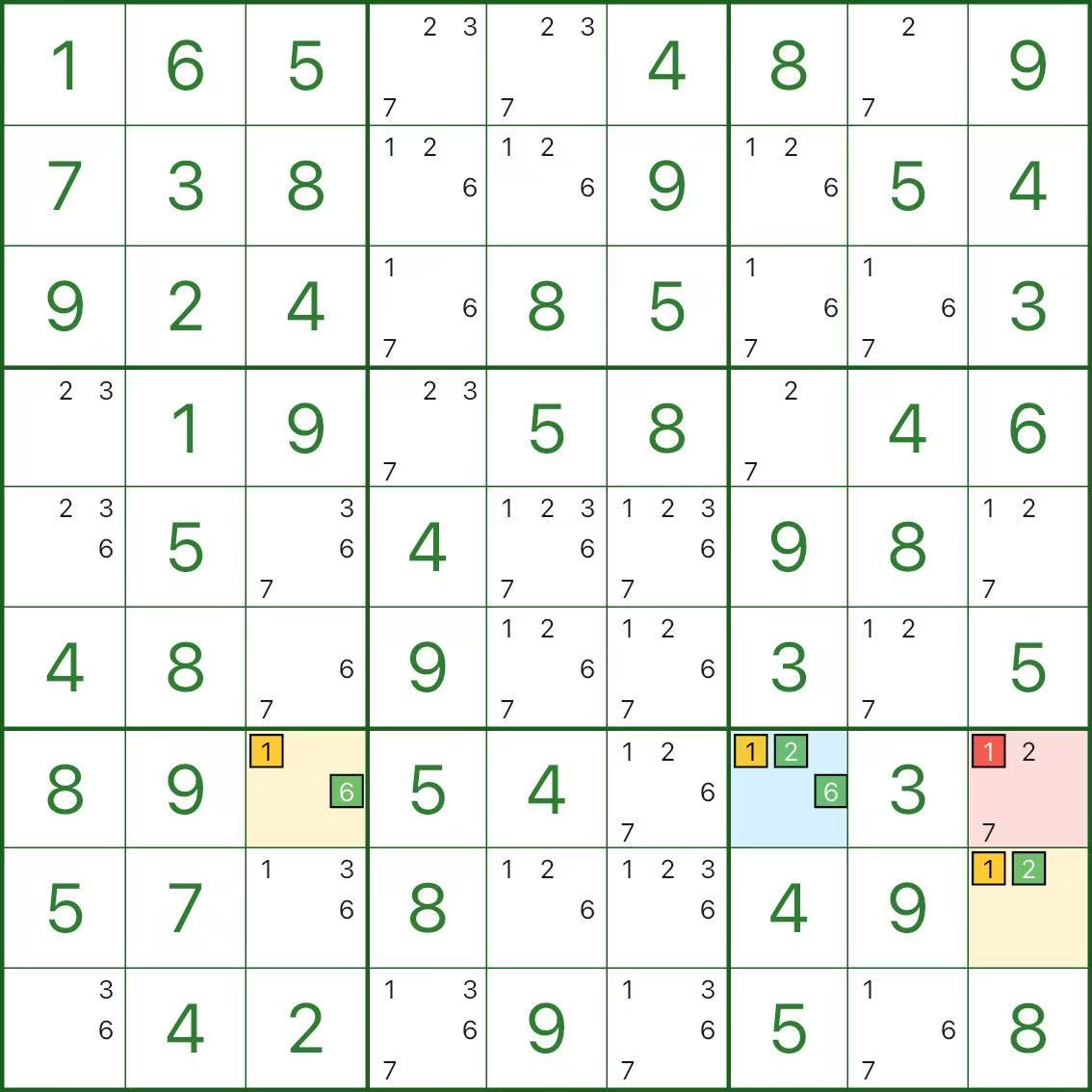
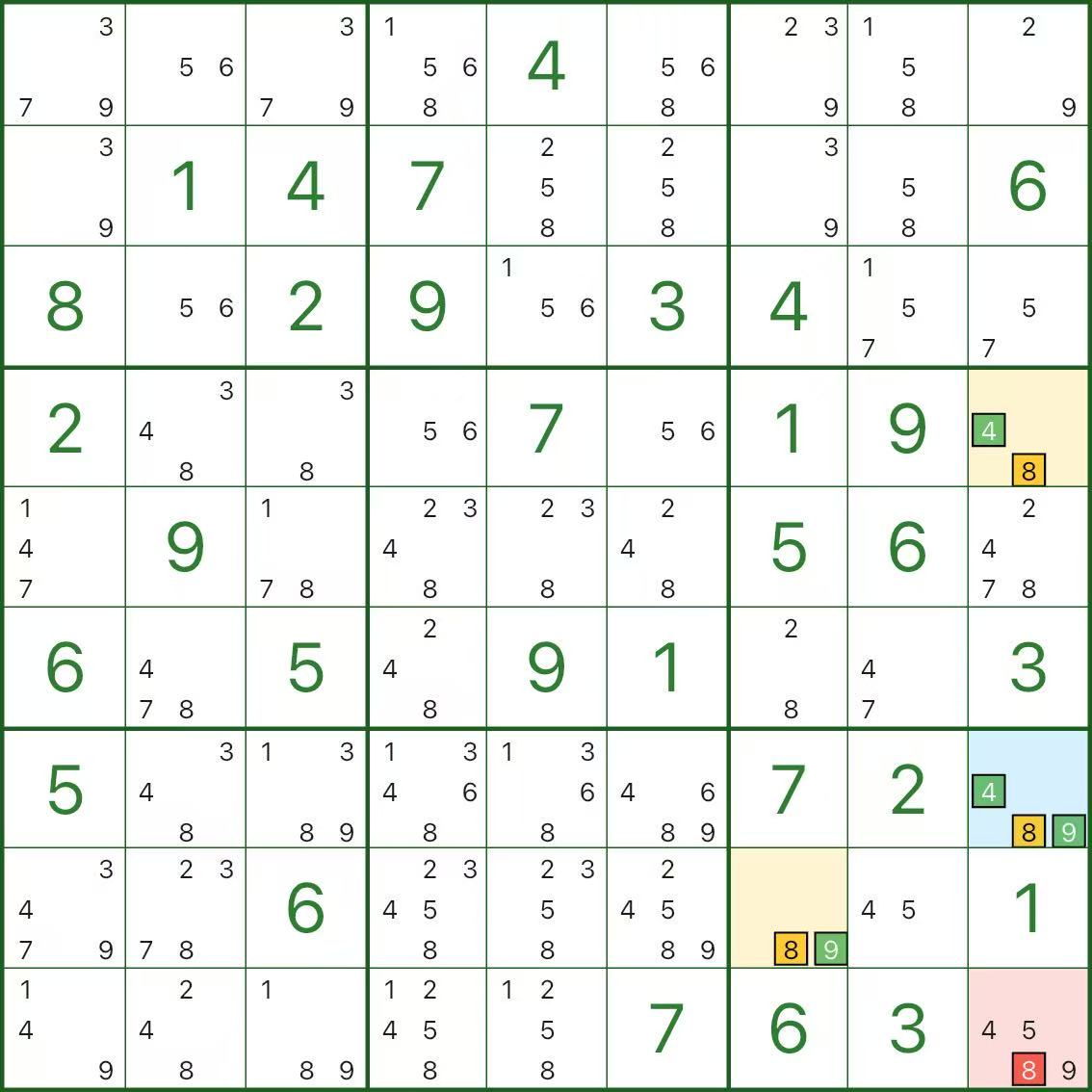
How to Find XYZ-Wing

One-line checklist: find a 3-candidate pivot {x,y,z}, find two bivalue wings {x,z} and {y,z}, then eliminate z from any cell that sees the pivot and both wings.

In a real puzzle:

1. Find a cell with exactly three candidates as the pivot (blue)
2. Find two cells that can see the pivot, each with exactly two candidates, shaped like {x,z} and {y,z} (yellow)
3. Find a cell that can see the pivot and both wings: remove candidate z there (red)